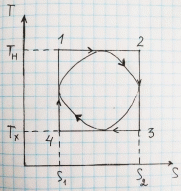Лабораторная работа № 113

ЦИКЛ КАРНО.

Выполнил: ст. гр. УГФ-19-01 Абдурахмонов М.

Принял: Хашаев М. М.

Цель работы: изучить на компьютерной модели цикла Карно для идеального газа.

Задание:

• 
  ознакомиться с компьютерной моделью, иллюстрирующей цикл Карно для идеального газа.
  
• 
  определить по данным, полученным на основе компьютерной модели цикла Карно:
  

1. 
   работу, совершённую газом за цикл;
   
2. 
   приведенное количество тепла;
   
3. 
   коэффициент полезного действия цикла Карно.
   

• 
  рассмотреть цикл Карно с точки зрения изменения энтропии.
  

Описание установки:

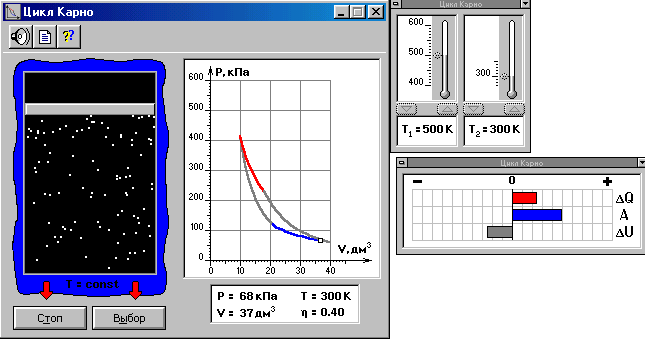Рис.1. Компьютерная модель цикла Карно для идеального газа.

Установкой в данной лабораторной работе является компьютерная модель, иллюстрирующая цикл Карно для идеального газа. Как видно из рис.1 данная установка представляет собой регулятор термометров, цикл Карно в системе координат P-V, а также значения термодинамических параметров и коэффициента вязкости в момент остановки процесса.

Методика выполнения работы:

1 . Вводим Т₁ и Т₂ из таблицы вариантов температур.Для этого нажимаем кнопку «ВЫБОР», перемещаем курсор так, чтобы его остриё находилось на кнопках регуляторов термометров или . Последовательными короткими нажатиями на эти кнопки устанавливаем заданные температуры нагревателя и холодильника. Записываем приведенное в окне опыта значение коэффициента полезного действия для выбранных температур.

2. Нажимаем кнопку «СТАРТ» и наблюдаем перемещение точки по замкнутой кривой цикла Карно.

3. Затем, нажав кнопку «СТОП», останавливаем процесс вблизи точки 2, которая соответствует переходу изотермического расширения газа в адиабатическое. Записываем в таблицу 2 значения V₂ и p₂, которые в момент остановки процесса в точке 2 будут обозначены в нижнем прямоугольнике окна опыта.

4. Аналогичные измерения проводим для состояний 3, 4 и 1 и записываем значения давлений и объёмов газа в соответствующие столбцы таблицы 2.

5. Повторяем измерения еще два раза. Данные записываем в строки 2 и 3 таблицы 2.

---

6. Повторяем весь цикл измерений ещё два раза. Результаты опытов заносим в таблицы 3 и 4, аналогичные таблице 2.

Обработка результатов измерений:

1. Для каждого из вариантов температур Т₁, Т₂ находим средние значения давлений (р₁, р₂, р₃ и р₄) и объемов (V₁, V₂, V₃ и V₄). Результаты записываем в таблицы 2,3,4.

2. Используя полученные средние значения давлений и объемов, находим для всех состояний (1, 2, 3, 4) и записываем результаты в соответствующие таблицы.
3. С помощью уравнения состояния идеального газа определяем число молей  газа в данной компьютерной модели. Оцениваем погрешность .
4. Рассчитываем Q₁, Q₂, A и записываем полученные значения в таблицу 5.

5. По формуле рассчитываем и записываем в таблицу 5 коэффициенты полезного действия цикла Карно для всех рассмотренных случаев.

6. Вычисляем приведенное количество тепла для всех процессов. Результаты записываем в таблицу 5.
7. Находим изменение энтропии для всех рассмотренных процессов.
8. Проанализировав полученные результаты, делаем выводы.
Ответы на контрольные вопросы:

1. В молекулярно-кинетической теории пользуются идеализированной моделью идеального газа, согласно которой считают, что:

1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;

2) между молекулами газа отсутствуют силы взаимодействия;

3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.

Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева): pV = νRT =(m/M)RT

2. Внутренняя энергия макросистемы – это функция состояния системы, т.е. она не зависит от предыстории системы и состоит из: суммарной кинетической энергии хаотического движения молекул; потенциальной энергии взаимодействия всех молекул системы; внутренней энергии частиц, составляющих систему.

Внутренняя энергия идеального газа

---

равна произведению средней энергии молекул газа < > к их числу N = N_A, где   число молей, N_A  число Авогадро (N_A = 6.0210²³моль^-1): U = N < >

3. Первое начало термодинамики: количество теплоты, сообщенное системе, идет на приращение ее внутренней энергии и на совершение системой работы над внешними телами.

4. Второе начало термодинамики (закон возрастания энтропии замкнутой системы при необратимых процессах): любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает.

5. Первое начало термодинамики для изотермического процесса: δQ = δA

Q = A₁₂=(m/M)RTln(V₂/V₁) = (m/M)RTln(p₁/p₂)

Первое начало термодинамики для адиабатического процесса: δA = -dU

pdV = -(m/M)C_VdT

6. Тепловые двигатели – это периодически действующие двигатели, совершающие работу за счет получаемого извне количества теплоты.

Основные элементы теплового двигателя: нагреватель, холодильник и рабочее тело.

7. Холодильник поглощает часть энергии рабочего тела, он нужен для того, чтобы работа, совершаемая телом за один цикл, была положительной. В двигателе внутреннего сгорания роль холодильника играет атмосфера.

8. Обратимые и необратимые процессы отличаются тем, что обратимый процесс допускает возможность возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения, а необратимый процесс не допускает такой возможности.

Все реальные процессы необратимы, потому что они протекают с конечной скоростью и сопровождаются трением, диффузией и теплообменом при конечной разности между температурами системы и внешней среды.

9. Энтропия – термодинамическая функция состояния, которая служит мерой беспорядка (неупорядоченности) системы.

---

Размерность энтропии равна Дж∙моль^-1∙K^-1.

10. Энтропия замкнутой системы может либо возрастать (для необратимых процессов), либо оставаться постоянной (для обратимых процессов).

Энтропия не замкнутой системы может вести себя любым образом.

11. Вероятностное определение энтропии: энтропия при абсолютном нуле температуры равна нулю.

12. Первая теорема Карно: коэффициент полезного действия тепловой машины, работающей по циклу Карно, зависит только от температур Т₁ и Т₂ нагревателя и холодильника, но не зависит от устройства машины, а также от вида используемого рабочего тела.

Вторая теорема Карно: КПД всякой тепловой машины не может превосходить КПД идеальной тепловой машины, работающей по циклу Карно с теми же самыми температурами нагревателя и холодильника.

13. Вывод формулы для коэффициента полезного действия цикла Карно:

Q_н=T_н (S₂ – S₁); Q_х=T_х (S₂ – S₁)

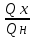η = 1 - = 1 -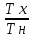

14. Пути повышения КПД тепловых двигателей: уменьшение потерь на трение сопрягающихся деталей, увеличение качества топлива и его сгорания, совершенствование систем отвода сгораемых газов.

15. Изотермический и адиабатический процессы и цикл Карно в системе координат T-S.

---

Смотрите также файлы

• Задание Опишите возможности системы обработки мультимедийных презентаций Microsoft Office Power Point. Ответ.docx

• То занимает урок.docx

• Москва 1994 Прутченков Александр Сергеевич.doc

• 4. Блага, удовлетворяющие потребности людей лишь в комплексе друг с другом в Процесс создания экономического блага и сопутствующее ему преобразование ресурсов.docx

• Для этого менеджеру необходимо.docx