МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЕ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Сибирский государственный университет науки и технологий

имени академика М.Ф. Решетнева»

Институт космической техники

институт/ факультет/ подразделение

Кафедра летательных аппаратов

кафедра/ цикловая комиссия

КУРСОВАЯ РАБОТА

По дисциплине «Строительная механика ракет»

дисциплина

Тема «Расчет сосуда высокого давления и ферменной конструкции»

тема (вариант)

Преподаватель _______________ А.В. Быков

подпись, дата инициалы, фамилия

Обучающиеся А17-01, 161411037 _______________ С.В. Орехов

номер группы, зачетной книжки подпись, дата инициалы, фамилия

Красноярск 2021

Содержание

1. 
   Расчет сосуда высокого давления 3
   

1.1 Расчет конической части 6

1.2 Расчет цилиндрической части 7

1.3 Расчет сферической части 8

1.4 Текст программы 9

Вывод 12

2. 
   Расчет ферменной конструкции 13
   

2.1 Текст программы в Maple.....................................................................20

Библиографический список................................................................................27

1. 
   Расчет сосуда высокого давления
   

Задание



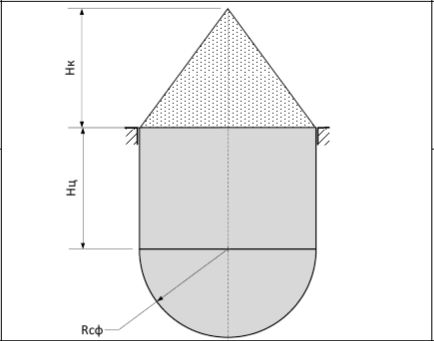
Рисунок 1.1 Вариант задания для расчета сосуда высокого давления

Дано:

• 
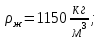
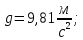
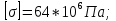
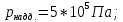
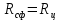
  Рассчитаем конический отсек, цилиндрический отсек и сферический отсек.
  
• 
  Для расчета используем метод сечений.
  

---

Список принятых обозначений
Обозначение	Величина (физический смысл)	Единица измерения	Индентификатор в тексте программы
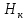	Высота конусной части	м	H_cone
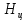	Высота цилиндрической части	м	H_cyl
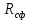	Радиус сферической части	м	R
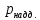	Давление наддува	Па	P
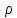	Плотность жидкости (жидкого кислорода)	кг/м3	Ro_hydr
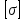	Допускаемое напряжение	Па	Sig_dop
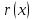	Радиус сечения конуса	м	r_cone
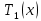	Меридиальное усилие конической части	Н/м	T1_cone
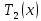	Окружное усилие конической части	Н/м	T2_cone
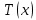	Эквивалентное усилие конической части	Н/м	T_EQ_cone
tmin	Минимальная толщина оболочки конической части	м	t_cone_min
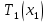	Меридиальное усилие цилиндрической части	Н/м	T1_cyl
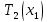	Окружное усилие цилиндрической части	Н	T2_cyl
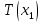	Эквивалентное усилие цилиндрической части	Н	T_EQ_cyl
tmin	Минимальная толщина оболочки цилиндрической части	м	t_min_cyl
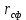	Радиус сечения сферической части	м	r_sph
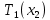	Меридиальное усилие сферической части	H	T1_sph
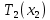	Окружное усилие сферической части	H	T2_sph
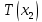	Эквивалентное усилие сферической части	H	T_EQ_sph
tmin	Минимальная толщина оболочки сф. части	м	t_min_sph

---

1.1 Расчет конического отсека



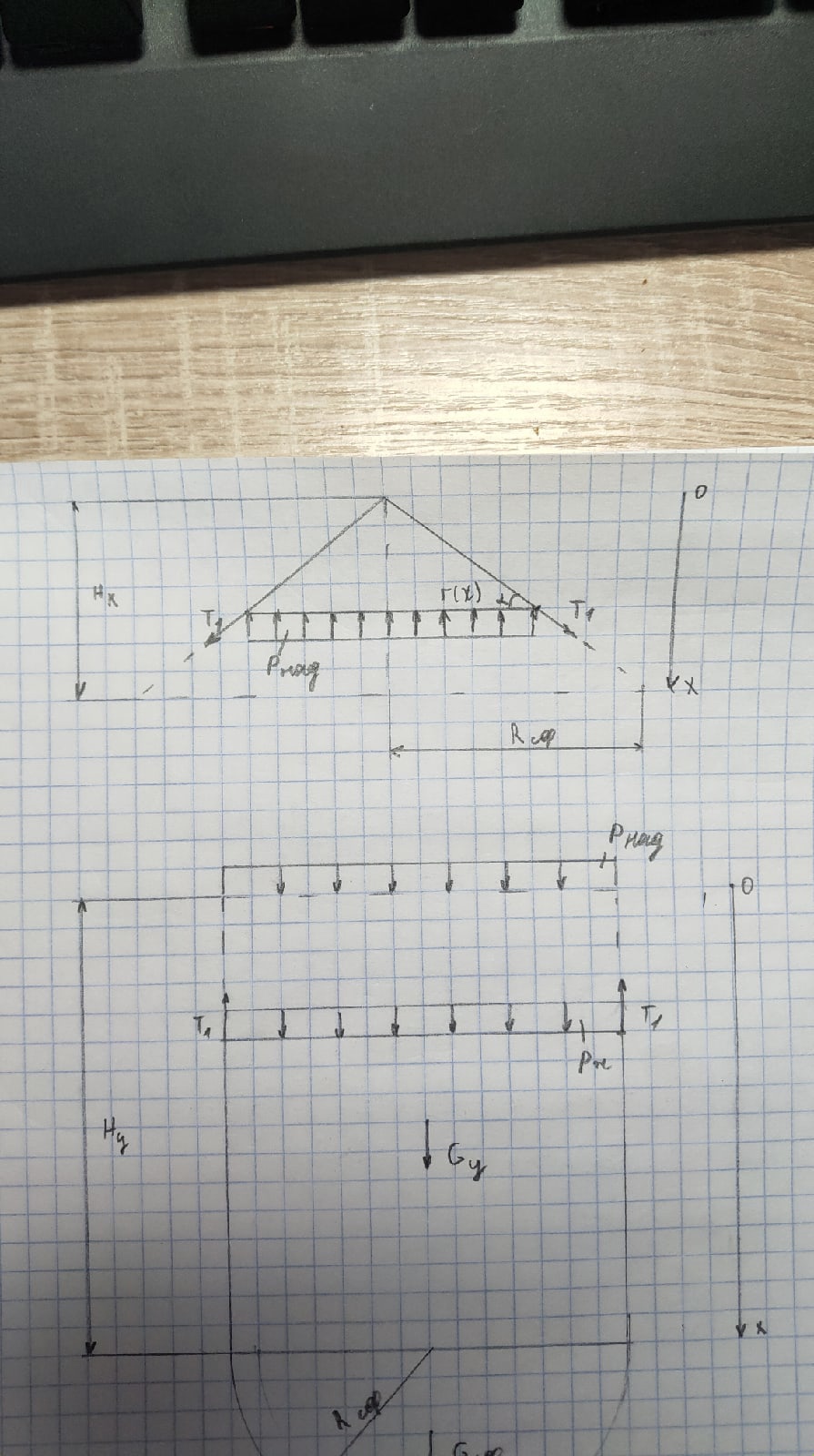
Рисунок 1.2. Расчет конической части методом сечения



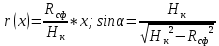
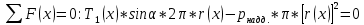-уравнение равновесия отсеченной части.

( )

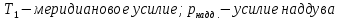Выразим меридиональное усилие:



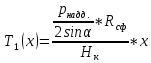
Запишем уравнение Лапласа для конической части и выразим окружное усилие ( ):

2. 
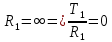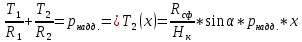
   Расчет цилиндрической части
   

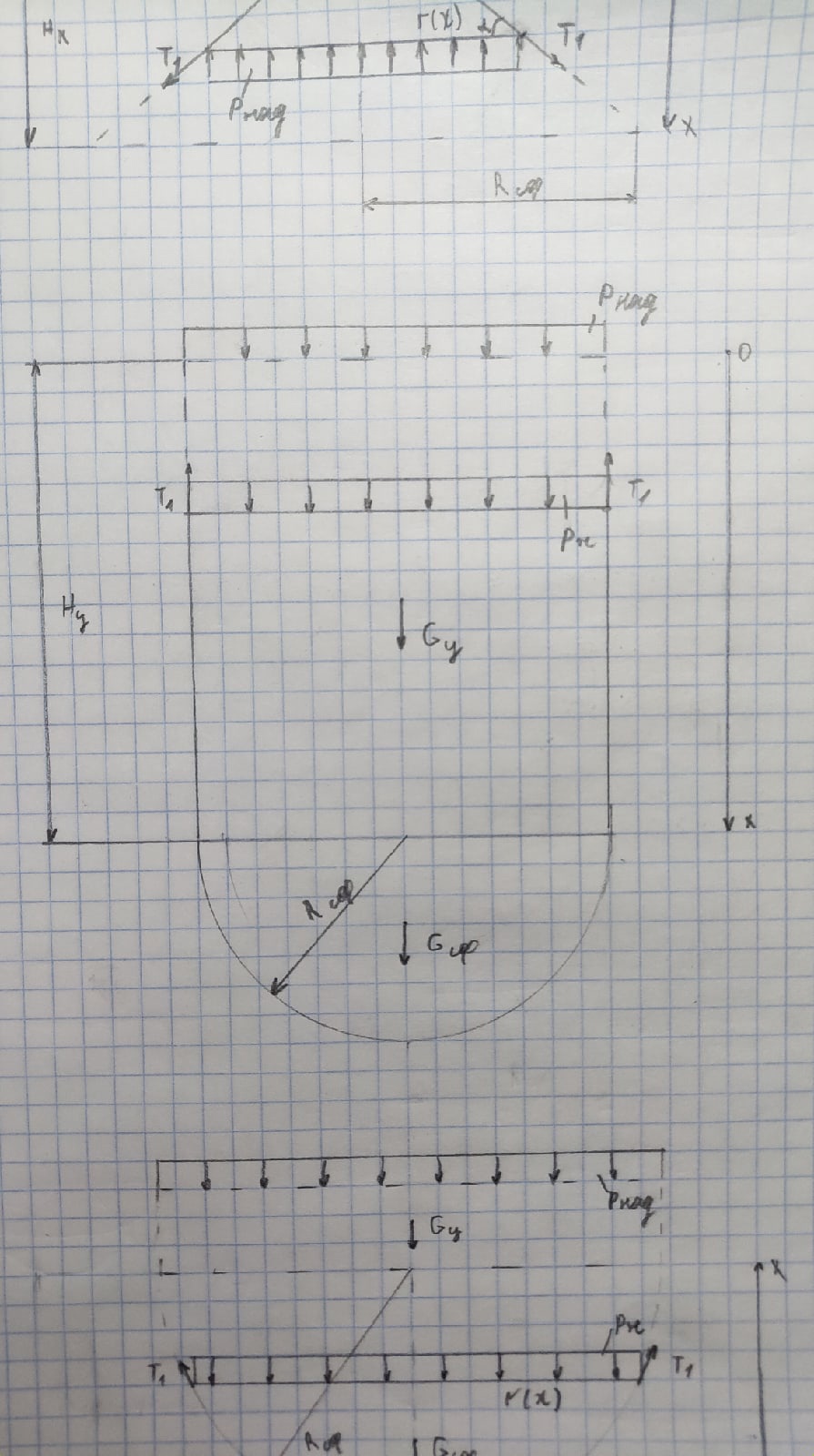
Рисунок 1.3. Расчет цилиндрической части методом сечения

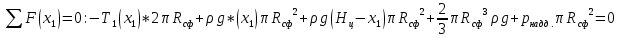– уравнение равновесия отсеченной части.

Выразим меридиональное усилие:



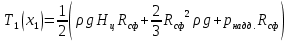
Запишем уравнение Лапласа для цилиндрической части и выразим окружное усилие ( ):

2. 
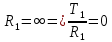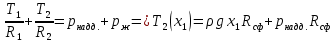
   Расчет сферической части
   

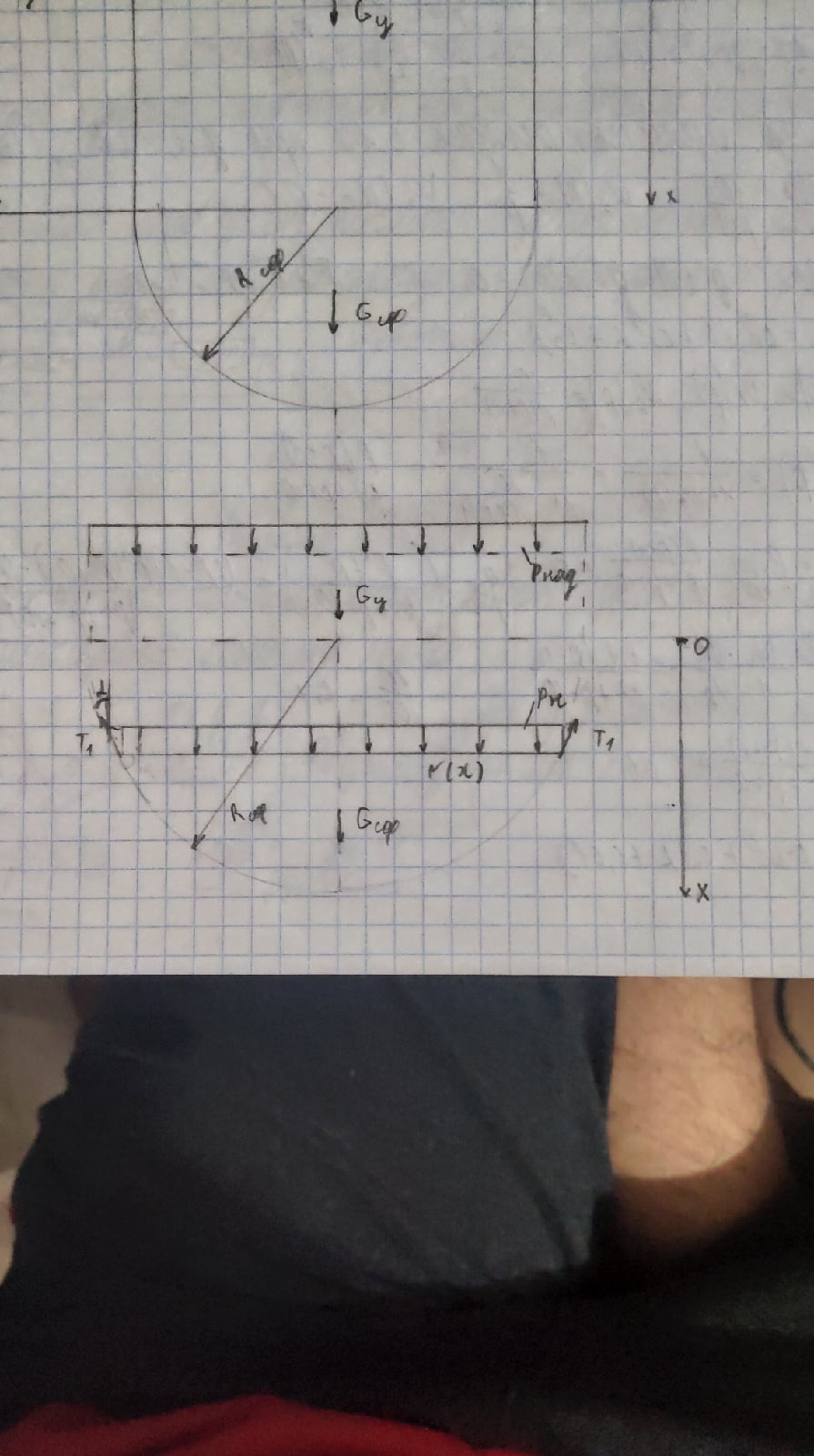
Рисунок 1.4. Расчет сферической части методом сечения



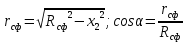
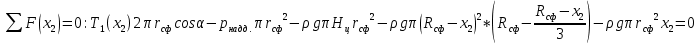– уравнение равновесия отсеченной части

Выразим меридиональное усилие:



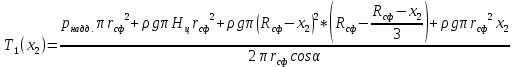
Запишем уравнение Лапласа для сферической части:

2. 
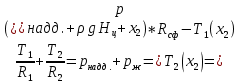
   Текст программы
   

> restart: with(linalg):

> # ________________Расчет сосуда высокого давления______

> # ________________ст. Орехов С.В.; гр. А17-01_________

---

> # ________________Начальные параметры_______________

> H_cone := 1: # Высота конуса, м

> H_cyl := 4: # Высота цилиндра, м

> R := 2: # Радиус сферы, м

> P :=5e5: # Давление наддува, Па

> Ro_hydr := 1140.0: # Плотность жидкости, кг/м3

> g := 9.81: # Ускор. своб. пад., м/с2

> Sig_dop := 64e6: # Допускаемое напряжение, МПа (переведено в Па)

> # ________________Расчет конической части(крышки) сосуда_______________

> r_cone:= x*(R/H_cone); # радуис конуса



> sin_a_cone:= H_cone/sqrt(H_cone^2 + R^2): # синус угла (alpha)

> EQ_cone1:= T1_cone*2*Pi*r_cone*sin_a_cone - P*Pi*(r_cone^2) = 0: # уравнение равновесия отсеч. части конуса

> assign(solve({EQ_cone1},{T1_cone}));

> R2_cone := r_cone/sin_a_cone:

> EQ_cone2:= T2_cone/R2_cone = P: # уравнение Лапласа для конической части оболочки

> assign(solve({EQ_cone2},{T2_cone}));

> T_EQ_cone:= sqrt(T1_cone^2+T2_cone^2-T1_cone*T2_cone):

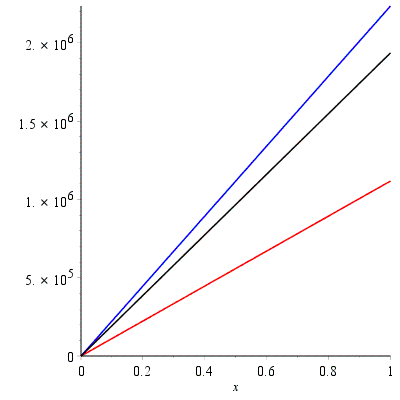
> plot([T1_cone,T2_cone,T_EQ_cone], x=0..H_cone, color=[red,blue,black]);


Т2

Тэкв

Т1

x,м

T,Н/м

> T_EQ_cone_0:= eval(T_EQ_cone, x=0):

T_EQ_cone_x:= eval(T_EQ_cone, x=H_cone):

T_EQ_cone_max:= max(T_EQ_cone_0, T_EQ_cone_x);



> t_cone_min:= T_EQ_cone_max/Sig_dop; # минимальная толщина оболочки, м



> # ________________Расчет цилиндрической части оболочки______________

> > EQ_cyl1:= T1_cyl*2*Pi*R = Ro_hydr*g*x1*Pi*R^2 + P*Pi*R^2+(H_cyl-x1)*Pi*R^2*Ro_hydr*g + ((2/3)*Pi*R^3*Ro_hydr*g): # уравнение равновесия цилиндрической части оболочки

>

> assign(solve({EQ_cyl1},{T1_cyl}));

> EQ_cyl2:= T2_cyl = ((Ro_hydr*g*x1)+P)*R; # уравнение Лапласа для цилидрической части оболочки



> assign(solve({EQ_cyl2},{T2_cyl}));

> T_EQ_cyl := sqrt(T1_cyl^2+T2_cyl^2 - T1_cyl*T2_cyl):

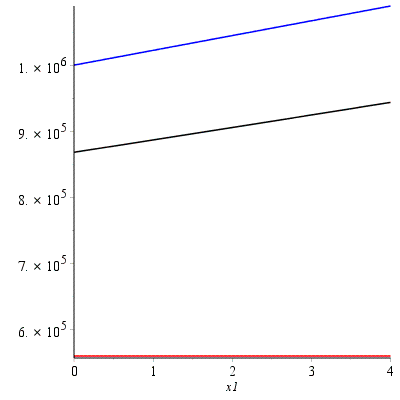
> plot([T1_cyl,T2_cyl,T_EQ_cyl], x1 = 0..H_cyl, color=[red,blue,black]);

---

Тэкв

Т2

Т1

x,м

T,Н/м


> > T_EQ_cyl_max := eval(T_EQ_cyl, x1 =H_cyl ); # эквивалентное напряжение



> t_min_cyl := T_EQ_cyl_max/ Sig_dop; # минимальная толщина стенки цилиндрической части сосуда



> #_________________Расчет сферической части сосуда_________________

> r_sph := sqrt(R^2-x2^2):

> cos_a_sph := r_sph/R:

> EQ_sph1 := + T1_sph*2*Pi*r_sph*cos_a_sph

> - Ro_hydr*g*(x2)*Pi*(r_sph^2)

> - Ro_hydr*g*H_cyl*Pi*(r_sph^2)

> - Ro_hydr*g* Pi*(R-x2)^2*(R-(R-x2)/3)

> - (P*Pi*r_sph^2) = 0: # уравнение равновесия стенки полусферической части сосуда

>

> assign(solve({EQ_sph1},{T1_sph}));

> EQ_sph2 := (T1_sph+T2_sph)/R = (Ro_hydr*g*(H_cyl+x2)) + P: # уравнение Лапласа для полусферической части сосуда

> assign(solve({EQ_sph2},{T2_sph}));

> T_EQ_sph := sqrt(T1_sph^2+T2_sph^2 - T1_sph*T2_sph):

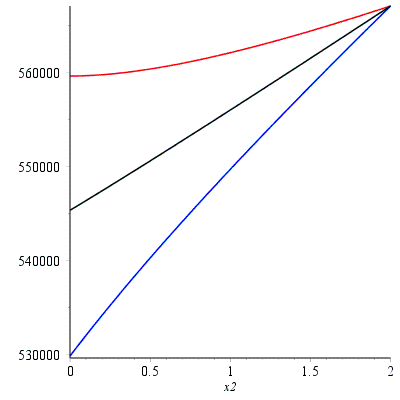
> plot([T1_sph,T2_sph,T_EQ_sph], x2 = 0..R, color=[red,blue,black]);


Т2

Тэкв

Т1

x,м

T,Н/м


> T_EQ_sph_dx:= diff( T_EQ_sph, x2 ):

> EQ_sph3 := T_EQ_sph_dx = 0 :

> sl:= solve( {EQ_sph3},{x2} ) ;



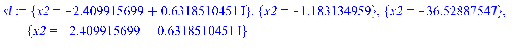
> x_extr:= rhs(sl[2][1]):

> T_EQ_sph_extr := eval(T_EQ_sph, x2 = x_extr):

> T_EQ_sph_x_R := eval(T_EQ_sph, x2 = R):

> T_EQ_sph_x_0 := eval(T_EQ_sph, x2 = 0):

> T_EQ_sph_max := max(T_EQ_sph_x_0, T_EQ_sph_extr, T_EQ_sph_x_R):

> t_min_sph:= T_EQ_sph_max / Sig_dop; # минимальная толщина стенки сферической части сосуда

---

Смотрите также файлы

• Почему в рп не должно быть полуфабрикатов и консервантов.doc

• Биография Фета. Основные мотивы лирики.docx

• Сообщение по окружающему миру заповедник Черные земли подготовила ученица 4 Б класса.pptx

• 1. к воинам Древнего Вавилона не относился.docx

• Социометрия как метод изучения межличностных отношений.docx