Файл: Министерство науки и высшего образование российской федерации.docx

Скачать файл (2,74Мб)

Заказать решение

ВУЗ: Не указан

Категория: Курсовая работа

Дисциплина: Не указана

Добавлен: 02.05.2024

Просмотров: 73

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

> tmin:=max(t_cone_min,t_min_cyl,t_min_sph);

Вывод: расчет сосуда высокого давления показал, что наиболее нагруженной является коническая часть СВД(основание конуса). Толщина в этом сечении будет определять толщину стенки всего сосуда. Минимальная толщина стенки:

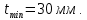
2. РАСЧЕТ ФЕРМЕННОЙ КОНСТРУКЦИИ

Дано:

L= 4 м

l= 4,447 м

P₁= 100 кН

P₂= 100 кН

P₃= 100 кН

P₄= 50 кН

P₅= 50 кН

d= 50 см (профиль стержня круглый) – диаметр стержня

E= 2*10¹¹ МПа – Жесткость стержня

[σ_доп]=195 МПа – допускаемое напряжение при растяженнии/сжатии для стали

Обозначение	Величина (физический смысл)	Единица измерения	Идентификатор в тексте программы
l	Длина стержней	м	l
L	Длина стержней	м	L
P₁	Сила приложенная к 2 узлу	Н	P1
P₂	Сила приложенная к 4 узлу	Н	P2
P₃	Сила приложенная к 6 узлу	H	P3
P₄	Сила приложенная к 9 узлу	H	P4
P₅	Сила приложенная к 9 узлу	H	P5
d	Диаметр сечения стержня	м	d
E	Жесткость	МПа	Е
F	Площадь сечения	м²	FF
N	Продольное усилие	Н	N
σ	Напряжение при растяжении/сжатии	МПа	Sgm

Таблица 2.1 – Список принятых обозначений
Найти: для каждого узла перемещения u и v, напряжения в стержнях. Растянутые стержни проверить на прочность, сжатые стержни проверить на прочность и устойчивость. Построить деформированный вид.

Решение: Задачу решаем методом конечных элементов. Пронумеруем узлы и стержни:

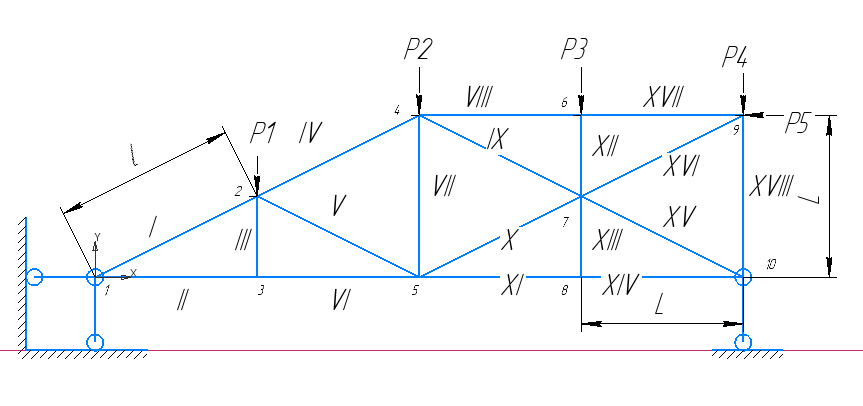Составляем глобальную матрицу жесткости К:

Составляем вектор узловых нагрузок:

аходим перемещения, решив уравение: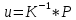

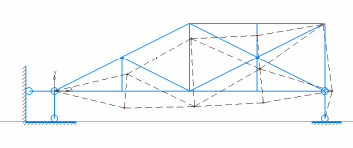
Рисунок 2.2 – Деформированный вид фермы

Рассчитаем продольные силы в стержнях, зная перемещения их узлов.

Используем формулу на примере 1 стержня:

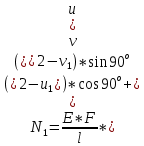
N₁= -328867.513383380 Н

Аналогично считаем для других стержней:

Растянутые стержни: 6, 8, 9, 10, 12, 13, 14, 15, 16
Сжатые стержни: 1, 2, 3, 4, 5, 7, 11, 17, 18

Проверяем стержни на прочность на примере 1:

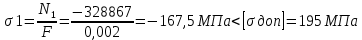
Аналогично проверяем другие:

Все стержни соответствуют условию прочности.
Вывод:

Вычислили перемещения в узлах ферменной конструкции. Сжатые и растянутые стержни проверили на прочность. Построили деформированный вид фермы.

2.1. ТЕКСТ ПРОГРАММЫ В MAPLE

> restart;

> with(LinearAlgebra):

> NE:=18; NU:=10;

> P1:= 100000; P2:= 100000; P3:=100000; P4:=50000; P5:=50000;

> E:=2.1e11;

> L:=0.40; h:=0.03; d:=0.05; a:=30; b:=-30; l:=0.447;

> FF:= Pi*d^2/4.0;

> J:=(h*d^3)/12;

> K:= Matrix(2*NU);

> MC:= Matrix(NE,4);

> MC:=<<1|2|l|a>,<2|3|L/2|90>,<2|5|l|b>,<2|4|l|a>,<4|5|L|90>,<5|7|l|a>,<4|7|l|b>,<6|7|L/2|90>,<7|8|L/2|90>,<7|9|l|a>,<7|10|l|b>,<9|10|L|90>,<1|3|L|0>,

<3|5|L|0>,<5|8|L|0>,<8|10|L|0>,<6|9|L|0>,<4|6|L|0>>;

> for ne from 1 to NE do

i:=MC[ne,1];j:=MC[ne,2];lc:=MC[ne,3];f:=MC[ne,4]*evalf(Pi)/180;

ac:=cos(f);bc:=sin(f);m:=2*(i-1);n:=2*(j-1);

k:=<,,<-ac^2|-ac*bc|ac^2|ac*bc>,<-ac*bc|-bc^2|ac*bc|bc^2>>;

k:=k/lc;

K[m+1..m+2,m+1..m+2]:=K[m+1..m+2,m+1..m+2]+k[1..2,1..2];

K[m+1..m+2,n+1..n+2]:=K[m+1..m+2,n+1..n+2]+k[1..2,3..4];

K[n+1..n+2,m+1..m+2]:=K[n+1..n+2,m+1..m+2]+k[3..4,1..2];

K[n+1..n+2,n+1..n+2]:=K[n+1..n+2,n+1..n+2]+k[3..4,3..4];od:

> for i from 1 to 20 do if (i=1 or i=2 or i=20) then for j from 1 to 2*NU do K[i,j]:=0.0; K[j,i]:=0.0; K[i,i]:=1.0; od; else fi; od;

>

>

> K:=E*FF*K;

> F := Vector(NU*2);

> F[1]:=0.0;F[2]:=0.0;F[3]:=0.0;F[4]:=-P1;F[5]:=0.0;F[6]:=0.0;F[7]:=0.0;F[8]:=-P2;F[9]:=0.0;F[10]:=0.0;F[11]:=0.0;F[12]:=-P3;F[13]:=0.0;F[14]:=0.0;

F[15]:=0.0;F[16]:=0.0;F[17]:=-P5;F[18]:=-P4;F[19]:=0.0;F[20]:=0.0;