Файл: Вопросы к экзамену по курсу высшей математики, 20222023 уч год.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.05.2024
Просмотров: 8
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вопросы к экзамену по курсу высшей математики, 2022-2023 уч. год
ВИШ «НМиТ» (Товароведение)
1. Матрицы и действия с ними. Свойства операций над матрицами.
2. Определители n-го порядка и их свойства.
3. Системы линейных уравнений, основные понятия. Метод Гаусса.
4. Ранг матрицы. Теорема Кронекера - Капелли. Решение неопределенных систем линейных уравнений. Общее и частное решения системы линейных уравнений.
5. Решение систем линейных уравнений с помощью правила Крамера.
6. Обратная матрица и способы ее нахождения.
7. Система линейных уравнений в матричном виде. Решение системы линейных уравнений с помощью обратной матрицы.
8. Векторы и линейные операции над ними. Арифметическое n -мерное векторное пространство
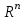: определение, свойства линейных операций над векторами.9. Скалярное произведение векторов и его свойства. Длина вектора, угол между векторами. Ортогональность двух векторов.
10. Линейно зависимые и линейно независимые системы векторов. Базис пространства
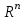. Координаты вектора в базисе.11. Различные виды уравнения прямой на плоскости (по точке и направляющему вектору прямой; по двум известным точкам прямой; по точке и вектору нормали прямой; по точке и угловому коэффициенту прямой).
12. Расстояние от точки до прямой. Условия параллельности и перпендикулярности прямых на плоскости.
13. Уравнение плоскости в пространстве. Расстояние от точки до плоскости.
14. Параметрические и канонические уравнения прямой в пространстве.
15. Понятие функции. Способы задания функций. Примеры. Элементарные функции. Графики основных элементарных функций.
16. Числовая последовательность. Предел числовой последовательности. Примеры.
17. Предел функции. Односторонние пределы. Арифметические свойства предела.
18. Первый замечательный предел. Второй замечательный предел.
19. Бесконечно малые и бесконечно большие функции. Эквивалентные бесконечно малые функции и их использование для вычисления пределов.
20. Непрерывность функции в точке. Арифметические операции над функциями, непрерывными в точке. Классификация точек разрыва. Примеры.
21. Функции, непрерывные на интервале (определение). Свойства функций, непрерывных на интервале.
22. Производная функции, ее геометрический, физический и экономический смысл. Уравнение касательной к графику функции. Дифференцируемость и непрерывность.
23. Основные правила дифференцирования. Производные основных элементарных функций.
24. Производная сложной функции. Производная обратной функции. Дифференциал функции.
25. Точки локального экстремума функции одной переменной. Теорема Ферма (необходимое условие экстремума функции). Достаточные условия экстремума.
26. Возрастание и убывание функции. Теорема о связи возрастания и убывания функции, дифференцируемой на интервале, со знаком её производной на этом интервале.
27. Выпуклость графика функции. Исследование направления выпуклости с помощью второй производной. Точки перегиба.
28. Правило Лопиталя.
29. Асимптоты. Общая схема исследования функций.
30. Первообразная. Теорема о множестве первообразных данной функции. Понятие неопределенного интеграла.
31. Свойства неопределенного интеграла. Табличные интегралы.
32. Замена переменной в неопределенном интеграле. Таблица дифференциалов.
33. Формула интегрирования по частям для неопределенного интеграла.
34. Понятие определенного интеграла. Геометрический смысл определенного интеграла.
35. Необходимое условие интегрируемости функции на отрезке. Классы интегрируемых функций. Свойства определенного интеграла.
36. Формула Ньютона - Лейбница. Замена переменной в определенном интеграле и интегрирование по частям.
37. Понятие функции нескольких переменных. Частные производные первого и второго порядка функции нескольких переменных.
38. Локальный экстремум функции нескольких переменных. Необходимое и достаточные условия экстремума.
