Файл: В курсовой работе проводится исследование частотных и переходных характеристик линейной электрической цепи. Определяется аналитическое выражение комплексной амплитуды напряжения и мгновенное значение напряжение.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.05.2024
Просмотров: 21
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Аннотация
В курсовой работе проводится исследование частотных и переходных характеристик линейной электрической цепи. Определяется аналитическое выражение комплексной амплитуды напряжения и мгновенное значение напряжение. Для решения поставленной задачи проводится анализ цепи методом контурных токов. Применение данного метода невозможно без проведения топологического анализа цепи, элементы которого представлены в работе. Результаты анализа позволяют определить требуемую комплексную передаточную функцию по току и переходную характеристику, а затем получить графики амплитудно-частотной и фазово-частотной характеристик (АЧХ и ФЧХ). Используя результаты проделанной работы, определить полосу пропускания, добротность, частоту и период собственных колебаний.
Summary
In the course work, a study of the frequency and transient characteristics of a linear electrical circuit is carried out. The analytical expression of the complex amplitude of the voltage and the instantaneous value of the voltage are determined. To solve the problem, the circuit is analyzed by the method of loop currents. The application of this method is impossible without a topological analysis of the circuit, the elements of which are presented in the work. The results of the analysis make it possible to determine the required complex current transfer function and transient response, and then obtain graphs of the amplitude-frequency and phase-frequency characteristics (AFC and PFC). Using the results of the work done, determine the bandwidth, quality factor, frequency and period of natural oscillations.
Содержание
введение 3
введение
Основная цель курсовой работы - систематизация, закрепление и углубление теоретических знаний, а также приобретение практических навыков аналитического расчета основных характеристик электрических цепей. Работа по курсу "Основы теории цепей" посвящена определению токов и напряжений в электрической цепи, а также анализу ее частотных и переходных характеристик. Анализ частотных характеристик может проводиться различными методами, например, контурных токов или узловых напряжений. Далее по полученным операторным функциям определяется комплексная передаточная функция и строятся графики ее частотных характеристик (АЧХ и ФЧХ). Большинство необходимых преобразований осуществляется с помощью математической системы MathCad, что существенно сокращает затраты времени и сил. Для анализа переходных характеристик электрических цепей существует ряд аналитических методов: классический, операторный, метод Дюамеля. В данной работе использовался операторный метод, основанный на использовании прямого и обратного преобразования Лапласа.
1. Анализ цепи и определение комплексной амплитуды напряжения U̇mc и мгновенного значения напряжения uc(t).
Используя метод контурных токов, найдём аналитическое выражение комплексной амплитуды напряжения U̇mc и мгновенное значение напряжения uc(t):
Согласно методу контурных токов, следует составить n = p–Nит–g+1 уравнений электрического равновесия цепи – узловых уравнений, (где g - количество узлов в цепи, р – количество ветвей, Nит – количество источников тока), в которых в качестве независимых переменных используются неизвестные токи независимых контуров. В качестве базисного выберем узел, к которому подключён источник тока. В исследуемой цепи g=3, р=5, Nит=1 поэтому количество уравнений, которые надо решать методом контурных токов: n=5-1-3+1=2. Воспользуемся операторной формой, обозначив j × ω через p. Обозначим контурные токи I11 и I22. Выберем их направление – они направлены против часовой стрелки. Нумерация узлов и направление токов показаны ниже.









I22
I11
I
2
1
0
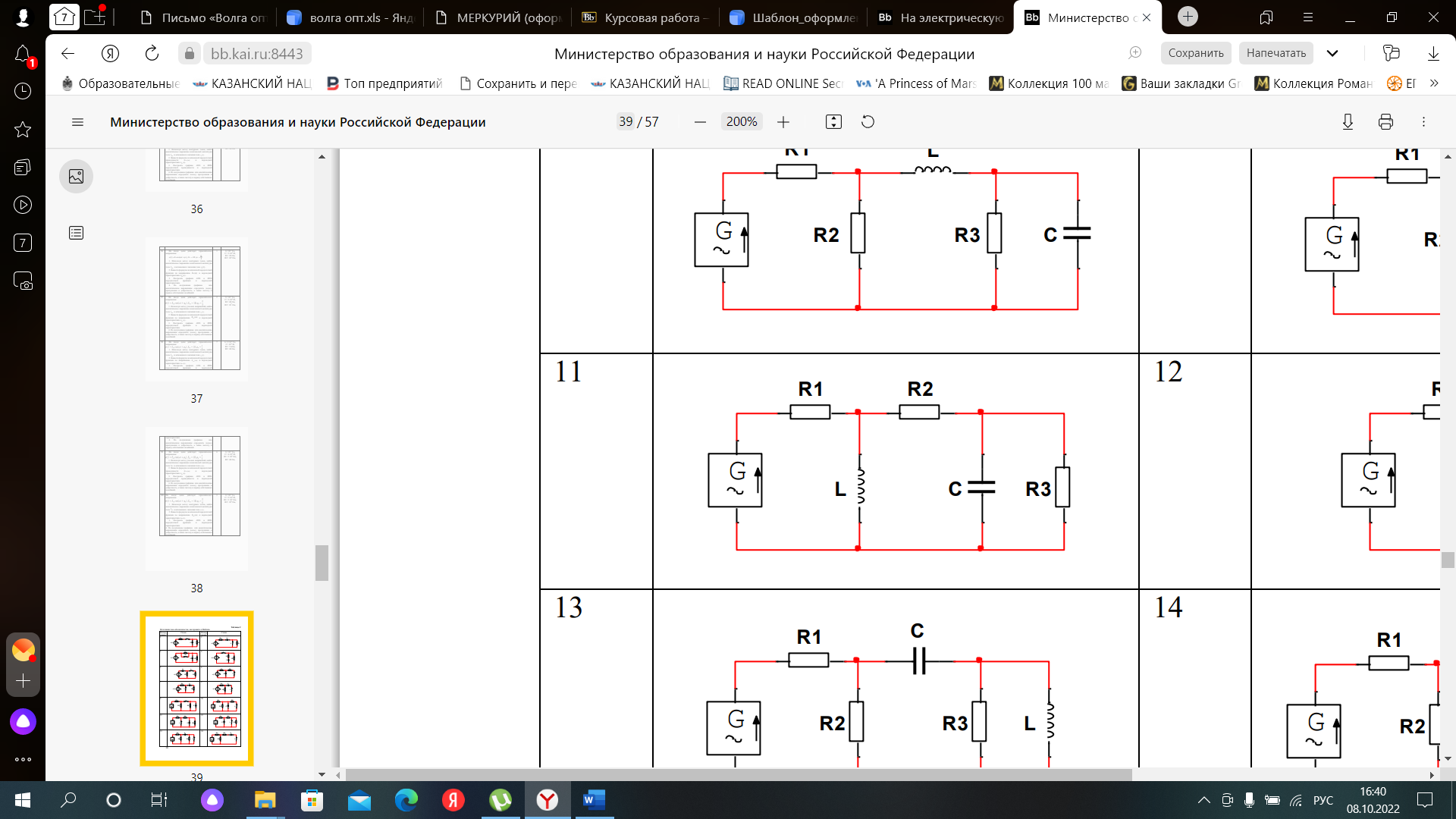
Используя Mathcad запишем уравнение для двух контуров согласно методу контурных токов. В таком случае система уравнений примет следующий вид:
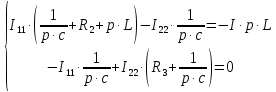 (1)
(1)Решим уравнение, используя аналитические возможности Mathcad:
i := -1
Given
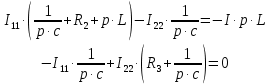

(2)
Find(I11, I22)
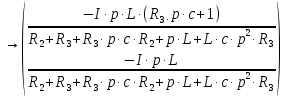


(4)
(3)
Заметим, что разность между İ11(ꞷ) и İ 22(ꞷ) равняется İmC(ꞷ):
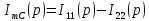
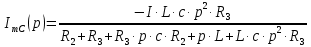
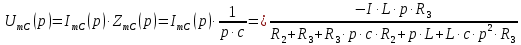

(5)
Перейдём к комплексной форме записи выражения (4):
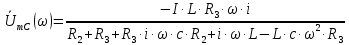

(6)
Представим комплексную амплитуду напряжения на конденсаторе (5), в показательной форме:
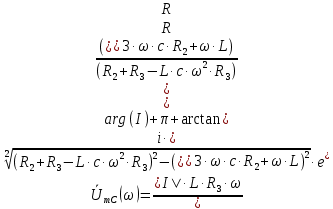
Запишем мгновенное значение напряжения
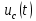 :
: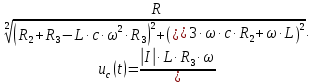
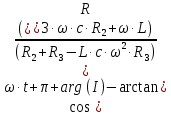

(7)
2. Вывод формулы комплексной передаточной функции по току KiC(ꞷ) и переходной характеристики hiC(t)

(8)
Получим комплексную передаточную функцию KiC(ꞷ) для этого запишем операторную передаточную функцию:
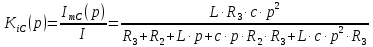

(9)
Перейдем к комплексной форме записи выражения (8):
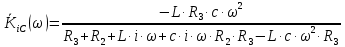
Представим функцию (9) в показательной форме:
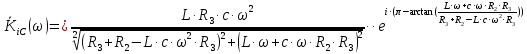

(10)
Амплитудно-частотная характеристика:
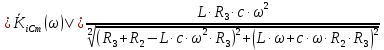
Фазово-частотная характеристика:
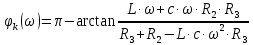
Определим диапазон частот, в котором следует строить графики АЧХ и ФЧХ. Для этого найдём полюсы передаточной функции (8) по току в операторной форме:
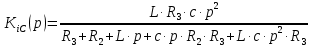
Обозначим р=x, а коэффициенты при «х» следующим образом:
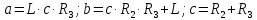
Полюсами функции являются корни выражения, которое находится в знаменателе формулы передаточной функции по току. Запишем знаменатель, используя введенные обозначения, и найдём корни этого выражения с помощью аналитических возможностей Mathcad. Будем при этом использовать заданные значения параметров схемы:
L= 10-3 Гн, C= 10-8 Ф, R1= 103 Ом, R2= 30 Ом, R3= 10 кОм
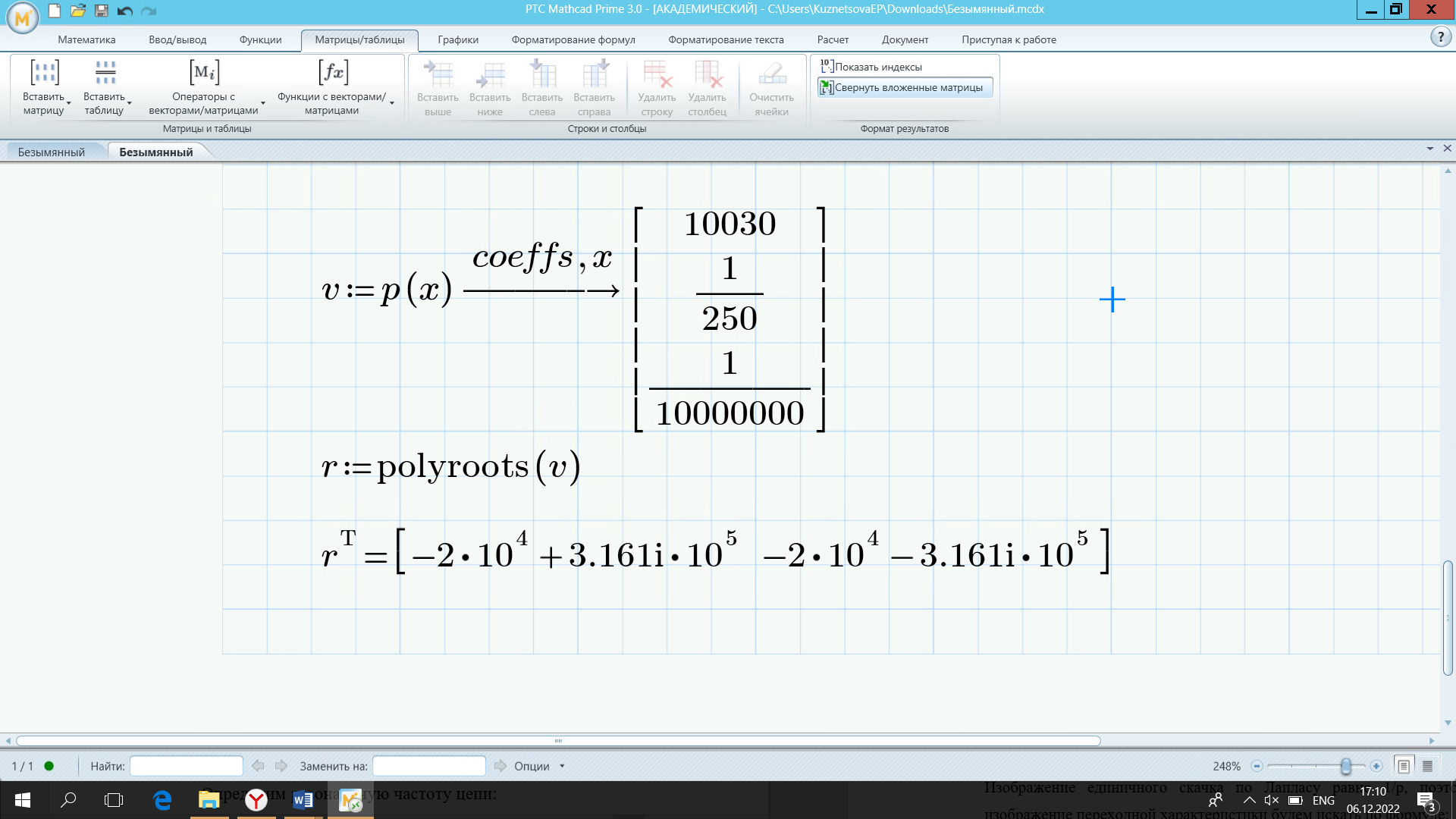
р1= -2×104 – 3.161i×105 p2= -2×104 + 3.161i×105

(11)
Определим резонансную частоту цепи:
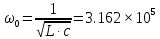 Рад/с
Рад/с Получились комплексно сопряжённые полюсы. Следовательно, расстояния от них до начала координат одинаковы. Оно равно:
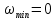
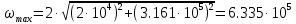 Рад/с
Рад/сСледовательно, частотные характеристики необходимо строить в диапазоне частот:
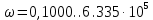 Рад/с
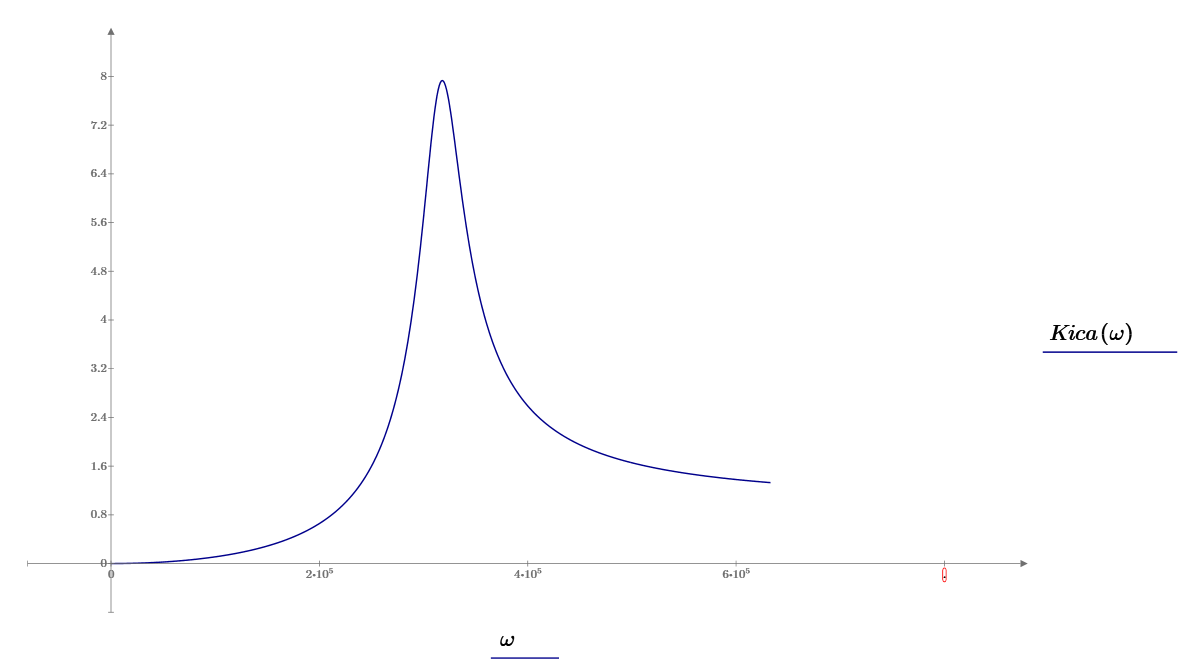
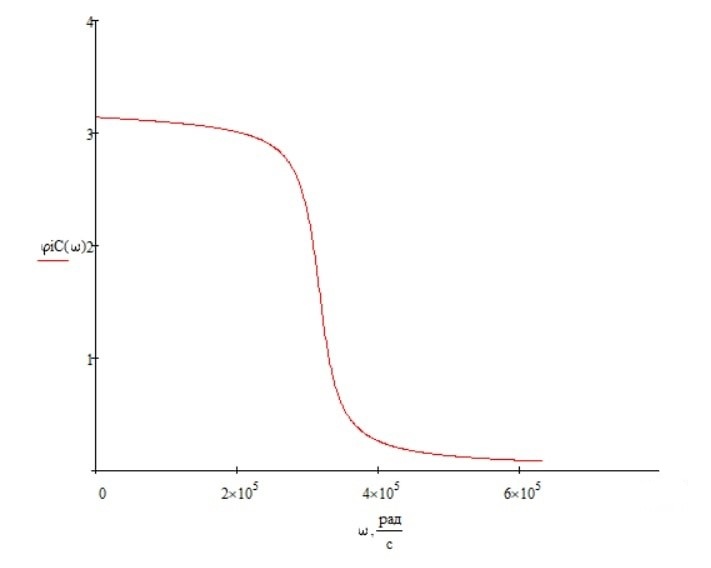
Рад/сИспользуя графические возможности Mathcad, построим графики АЧХ и ФЧХ с помощью функций Mathcad:
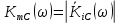
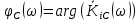
В результате получим следующие графики:
Амплитудно-частотная характеристика схемы:

Фазо-частотная характеристика схемы:
3. Определение переходной характеристики h_iC (t) и построение ее графика

(12)
Переходная характеристика определяется как отклик цепи на единичный скачок. Изображение единичного скачка по Лапласу равно 1/р, поэтому изображение переходной характеристики будем искать по формуле:
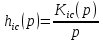

(13)
Тогда изображение переходной характеристики цепи с учетом формулы (8) будет иметь следующий вид:
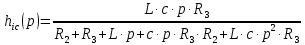
Обозначим числитель и знаменатель функции (13) следующим образом:
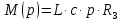
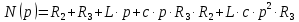
Корни знаменателя были найдены ранее:
р1= -2×104 – 3.161i×105
p2= -2×104 + 3.161i×105

(14)
Получили два различных простых корня – полюсы знаменателя, поэтому переходная характеристика должна быть определена по формуле:
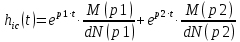
Где dN(p) – производная знаменателя:
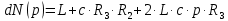
Найдём численное значение dN(p) по формуле для каждого из трех корней:
dN(p1) = -0.063i
dN(p2) = 0.063i

(15)
С помощью аналитических возможностей Mathcad определим переходную характеристику. В результате получим очень объёмное выражение, которое, однако, можно представить и в компактном виде, округлив десятичные дроби до трёх знаков после запятой. Тогда переходная характеристика примет следующий вид:
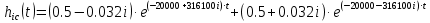
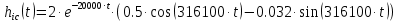
Определим временной интервал 0÷Т1, в котором надо рассчитать переходную характеристику:
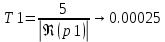 c
c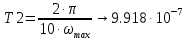 c
cСледовательно, график переходной характеристики необходимо строить во временном интервале:
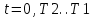
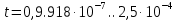 c
cГрафик переходной характеристики:
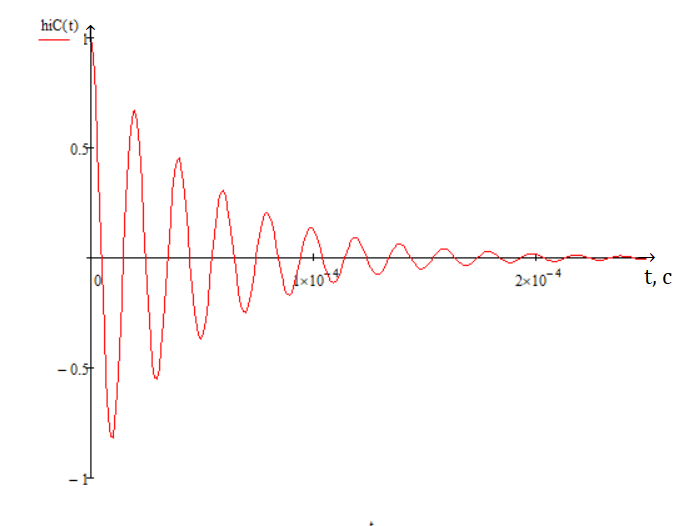
4. Определение полосы пропускания и добротности, а также частоты и периода собственных колебаний.
Полоса пропускания определяется по диапазону частот, в котором передаточная функция
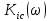 не опускается ниже уровня 0.707 от своего максимального значения
не опускается ниже уровня 0.707 от своего максимального значения 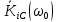 :
:Период собственных колебаний в контуре:
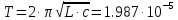 с
сЧастота собственных колебаний в контуре:
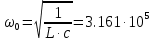 c-1
c-1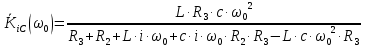
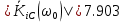
С учетом сказанного, уровень, на котором выполняется требуемое условие, определится как произведение максимального значения 0.707, в данном случае на уровне 5.588. для определения граничных частот полосы пропускания воспользуемся возможностями MathCad:
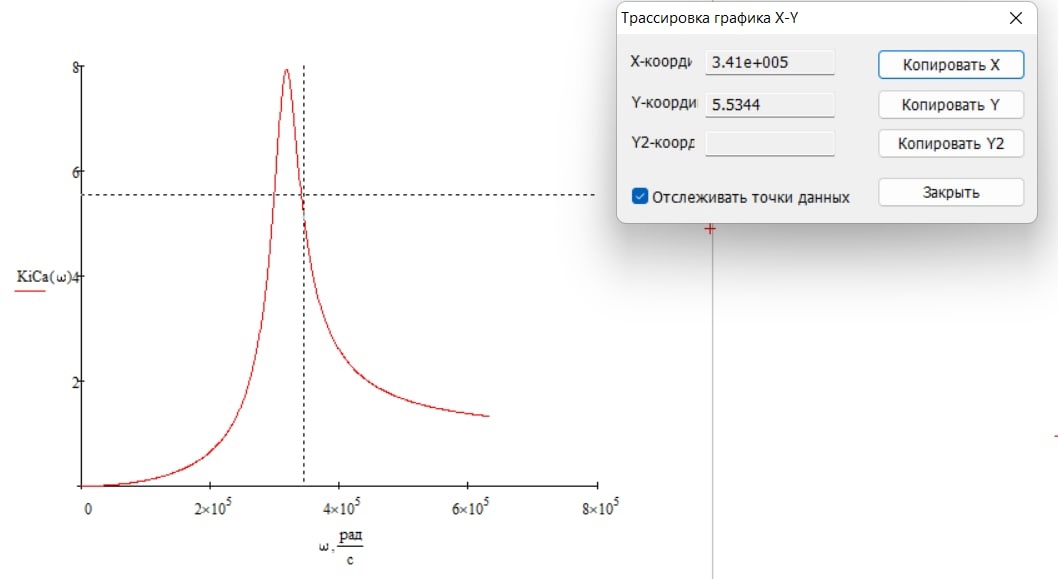
Определение верхней частоты по АЧХ
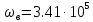 Рад/с
Рад/с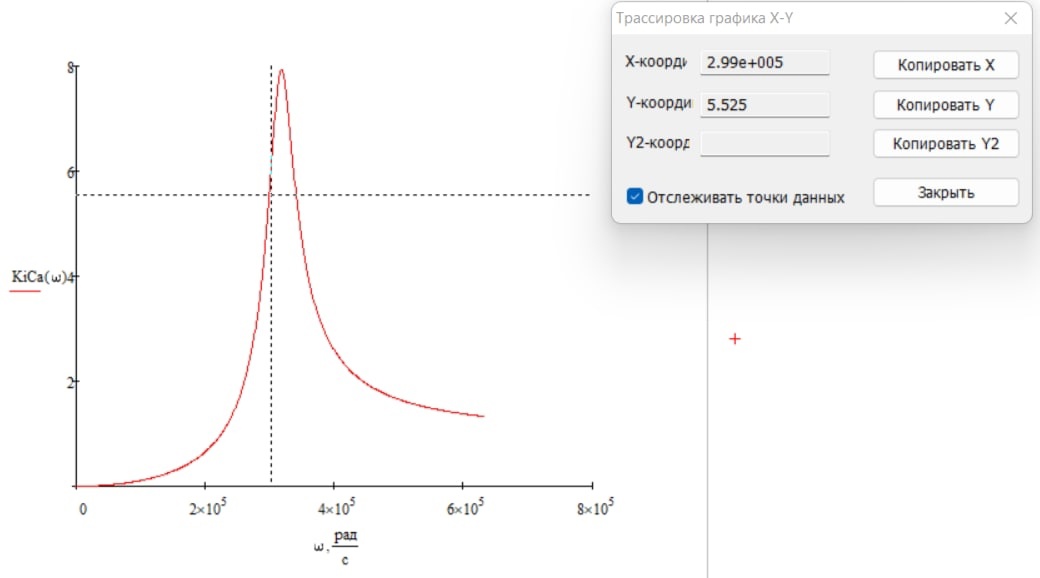
Определение нижней частоты по АЧХ
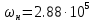 Рад/с
Рад/с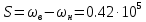 Рад/с
Рад/сПолоса пропускания контура при фиксированном значении резонансной частоты
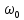 обратно пропорциональна его добротности Q и не зависит от емкости C, зная это можем вывести формулу добротности и подставляя ранее найденные значения, можно найти значение добротности:
обратно пропорциональна его добротности Q и не зависит от емкости C, зная это можем вывести формулу добротности и подставляя ранее найденные значения, можно найти значение добротности: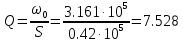
ЗАКЛЮЧЕНИЕ
В процессе выполнения курсовой работы была составлена и решена с помощью аналитических возможностей Mathcad система уравнений по методу узловых напряжений. Решение составленной системы позволило найти комплексную амплитуду U̇mС и мгновенное значение напряжения uС(t), а так же комплексной передаточной функции по току KiC(ꞷ) и переходной характеристики hiC(t), для которой были построены графики АЧХ и ФЧХ.
Для нахождения переходной характеристики напряжения на ёмкости hiC(t) и построения её графика использовали операторный метод. Полученная характеристика имеет колебательный характер, а амплитуда напряжения на конденсаторе U̇mС экспоненциально уменьшается во времени.
При помощи графика амплитудно-частотной характеристики были найдены добротность и полоса пропускания, а по графикам переходной характеристики период и частота собственных колебаний.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
-
Соколов С.В. Электроника. [Электронный ресурс] / С.В. Соколов, Е.В. Титов. – Электрон. дан. – М.: Горячая линия-Телеком, 2013. – 204 с. – Режим доступа: http://e.lanbook.com/book/63245. -
Иванов М.Т. Радиотехнические цепи и сигналы: учебник для студ. вузов / М.Т. Иванов, А.Б. Сергиенко, В.Н. Ушаков. – СПб.: Питер, 2014. – 336 с. -
Попов В.П. Основы теории цепей: Учебник для вузов/ В.П. Попов. – 5-е изд., стереотип. – М.: Высшая школа, 2005. – 575 с. -
Угрюмов Е.П. Цифровая схемотехника: учеб. пособие для студ. вузов / Е.П. Угрюмов. – 3-е изд., перераб. и доп. – СПб.: БХВ-Петербург, 2010. – 816 с.
