ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 50
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3. ЛАБОРАТОРНЫЕ РАБОТЫ
3.1 Тематика лабораторных работ
| № раздела (модуля) | Тема лабораторной работы |
| 5 | Нагрев металла в методической печи с учетом образования окалины |
| 5 | Нагрев и охлаждение тел простой формы |
| 5 | Расчет расходов воды на секции зоны вторичного охлаждения |
3.2 Методические рекомендации для выполнения лабораторных работ
Лабораторная работа №1 Нагрев металла в методической печи с учетом образования окалины
Цель работы: Исследовать влияние температуры дымовых газов в методической печи на температуру нагрева заготовки, перепад температуры по ее толщине и толщину окалины
Задачи работы:
-
ознакомиться с математической моделью нагрева слябов в методической печи, -
определить рациональный режим нагрева металла в печи, -
изучить динамику нагрева металла при рациональном режиме нагрева.
-
Математическая модель нагрева металла в методической печи
Модель предназначена для прогноза распределения температуры по толщине наблюдаемого сляба, а также толщины окалины, при следовании сляба вдоль печи при заданной температуре среды в ее зонах. Печь состоит из трех зон нагрева сверху (методической, сварочной и томильной) и одной зоны нагрева снизу (рис. 1.1.а);
Рис. 1.1. Схема четырехзонной печи (а)- расчетное сечение (б) и его дискретизация (в): I-IV-зоны печи; 1-слябы, 2-расчетное сечение сляба,
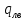и 
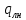-потоки тепла излучением сверху и снизу, ОЗ и ОВ окна загрузки и выдачи слябов ; I-Nвнутренние узлы, 0,
N+1- фиктивные узлы, i и n –индексы дискретных величин координаты и времени.
Длина нижней зоны совпадает с длиной первых двух верхних зон. Наблюдаемый сляб загружается в печь и следует по печи с заданной скоростью. Нагрев сляба в каждой зоне осуществляется излучением от среды, которая характеризуется эффективной температурой зоны. Конкретные значения этой величины в данной зоне зависит от расхода топлива на зону. Температура среды по длине зоны не изменяется.
При математическом описании процесса нагрева сляба приняты следующие физические допущения:
-
сляб движется по печи со скоростью, заданной кусочно-постоянной функцией от времени; -
температура среды, нагревающей сляб, изменяется по заданному временному графику, зависящему от расположения сляба в печи в конкретный момент времени; -
поток тепла теплопроводностью в слябе вдоль и поперек печи отсутствует; -
начальная температура в слябе равномерная; -
теплофизические свойства металла зависят от температуры; -
потоками тепла от сляба в нижнюю кладку в томильной зоне можно пренебречь; -
коэффициент излучения, характеризующий теплообмен в печи, принимается постоянным для всех зон.
С учетом этих допущений математическое описание процесса нагрева включает уравнение теплопроводности:
, (1)где
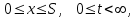Т - температура, К,граничные условия вида:
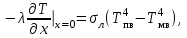(2)
(3) начальное условие: Т(х,0) = То = const, и уравнение роста окалины в форме:
(4)где S- толщина сляба, t - время, х - координата по толщине сляба, отсчитываемая от верхней поверхности, Т(х, t) - распределение температуры по толщине сляба в момент времени t,
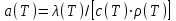- температуропроводность стали, 
- теплопроводность стали,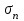 
- коэффициент излучения, Тпв
и Тпн - температура печи в верхней и нижней зонах, Тмв и Тмн - температура верхней и нижней поверхностей сляба, z - координата положения сляба в печи, отсчитываемая от точки посада:
lн - длина нижней зоны, То - начальная температура сляба, kо и Мо - эмпирические коэффициенты, 
- толщина окалины.На рис. 1.1 показаны схемы печи, расчетное сечение и его дискретизация. Дискретный конечноразностный аналог (приближенная модель) приведенной математической модели включает формулы для расчета поля температуры
во внутренних узлах расчетной области по известному полю температуры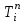 
. 
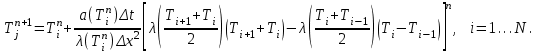(5)- температуры в фиктивном узле i= 0:
(6)где:
, 
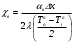- температуры в фиктивном узле i= N+1:
(7)где:
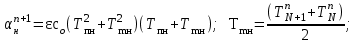
- температуры в начальный момент времени n = 0:
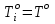(8)- толщины окалины в n+1 момент времени:
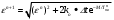(9)Здесь:
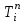- температуры в n-ный момент времени в i-том узле, 
- количество внутренних узлов,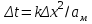 
, k<0,5 - коэффициент устойчивости явной разностной схемы аппроксимации, ам - максимальное значение температуропроводности.Расположение сляба в печи в момент времени n+1, определяется по формуле:
Тпв и Тнн находятся по графикам кусочно-постоянных функций от времени.
Теплофизические свойства стали аппроксимируются кусочно-линейными функциями и представляются в табличной форме.
Алгоритм решения приближенной модели включают следующие операции:
-
ввод данных,
-
расчет выражений, независящих от t и x, -
заполнение n-ного поля температуры начальным значением температуры, счетчиков времени и номера печати, -
начало цикла по времени: суммирование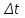
к счетчику времени, -
определение Тпв и Тнн оп текущему времени в счетчике времени с использованием графиков кусочно-постоянных функций от времени, расчет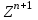
, -
расчет поля температуры во временных узлах для момента времени n+ 1 по формуле (7), -
расчет температуры в фиктивных узлах и толщины окалины по результатам (6) и (7), -
пересылка поля n+1 момента в полеn момента, -
решение на печать, которое выдается через заданный интервал времени (если решение не принято, переход на п.11), -
если решение принято, то печать n+1 поля и добавление +1 к счетчику печати, -
решение на конец счета и печать, если координата положения сляба вышла за пределы печати, -
в противном случае - переход на п.4.
Алгоритм запрограммирован на языке TURBO BASIC. Программа (компьютерная модель) хранится в файле PETCH.BAS и работает в среде ТВ. EXE, который находится в директории BLACKBOX. Идентификаторы исходных данных к программе представлены в табл . П.2. Результаты моделирования в виде поля температуры в узлах расчетной области и других данных через равные интервалы времени выдаются на экран компьютера. Идентификаторы результатов печати, выводимых на экран, находятся в табл. 2.2.
Порядок использования компьютерной модели следующий:
-
После включения компьютера входим в директорию BLACKBOX, затем KBASIC и запускаем файл ТВ. EXE. -
В меню ТВ. EXE входим в режим работы FILE (в падающем меню), запрашиваются все файлы с расширением BAS и выбирается PETCH.BAS. -
Затем, после отмены FILE клавишей ESC, выбирается режим EDIT и заполняются исходными данными все операторы DATA. -
После отмены режима EDIT клавишей ESC, устанавливается режим RUN и запускается программа. -
После выдачи данных на экран через заданный шаг времени программа останавливается; для продолжения работы нажимается клавиша “пробел”. -
По окончании счета программа выходит в режим RUN.
Таблица 2.1
Идентификатора исходных данных к программе
| № п/п | Идентифи-катор | Обозна-чение | Название величины | Размер-ность |
| 1 | s | S | толщина сляба | м |
| 2 | t0 | to | начальная температура сляба | оС |
| 3 | sl |  | коэффициент лучистого теплообмена в печи |  |
| 4 | dp | 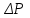 | интервал времени печати | сек |
| 5 | hk | hk | общая длина всех верхних зон нагрева (длина печи) | м |
| 6 | hn | hн | общая длина всех нижних зон нагрева (длина нижней зоны) | м |
| 7 | k0 | ko | постоянная из уравнения роста окалины (=250) | м2оС/с |
| 8 | m0 | mo | постоянная из уравнения роста окалины (=4000) | оС |
| 1 | n | N | количество внутренних узлов в слябе (массив температур) | шт |
| 2 | q | q | количество узлов в массиве функции температуропроводности | шт |
| 3 | c | c | количество узлов в массиве функции теплопроводности | шт |
| 4 | 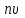 | 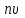| количество узлов в массиве функции скорости движения слябов | шт |
| 5 | np | np | количество зон нагрева сверху и снизу | шт |
| 6 | kx | kx | коэффициент устойчивости при расчете шага по времени | безразм. |
| Массивы | ||||
| 1 | ta(q) | T | массив температуры для табличной функции а=а(Т) | оС |
| 2 | a(q) | a(T) | массив значений коэффициентов температуропроводности для табличной функции а=а(Т) | м2/с |
| 3 | tl(c) | T | массив температуры для табличной функции  | оС |
| 4 | l(с) |  | массив значений коэффициентов теплопроводности для табличной функции  | Вт/моК |
| 5 | 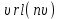 | t | массив значений времени в табличной функции  | |
| 6 |  | 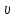 (t) | массив значений скорости движения сляба для табличной кусочно постоянной функции | м/с |
| 7 | 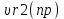 | t | массив значений времени в табличной кусочно постоянной функции Тпечи = F(T) | сек |
| 8 | 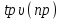 | Тпв | массив значений температуры печи сверху сляба во времени | оС |
| 9 | tpn(np) | Тпн | массив значений температуры печи снизу сляба во времени | оС |
Таблица 2.2
Идентификаторы результатов расчета
| № п/п | Идентифи-катор | Обозна-чение | Название величины | Размер-ность |
| 1 | р | Р | номер печати | безразм. |
| 2 |  r | t | текущее время следования сляба в печи | сек |
| 3 | h | h | расстояние от начала печи до его местонахождения в печи | м |
| 4 | 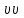 | | скорость движения сляба в момент t | м/с |
| 5 | Z2 |  | толщина окалины сверху сляба вк моменту времени t | |
| 6 | tp 2 | Тпв | температура печи сверху в момент t | оС |
| 7 | tpn2 | Тпн | тоже снизу | оС |
| 8 | tm | Тпов.в | температура верхней поверхности сляба в момент t | оС |
| 9 | tmn | Тпов.н | тоже нижней поверхности | оС |
-
Определение рационального режима нагрева металла
Изложенная модель используется для определения рационального режима нагрева металла в печи.
Под режимом нагрева металла в печи здесь понимается набор значений температуры нагревающей среды в четырех зонах. Рациональным режимом назовем такой, при котором обеспечиваются допустимые по условиям прокатки температура верхней поверхности сляба и перепад температур по толщине сляба, а также минимальная толщина окалины, при выдаче сляба из печи.