ФГБОУ ВО

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ «МЭИ»





КАФЕДРА ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ СИСТЕМ

КУРСОВОЙ ПРОЕКТ ПО КУРСУ «ЭЛЕКТРОСНАБЖЕНИЕ».
Вариант 5.
Шифр 15631.

Выполнил:
Группа:
Проверил:

МОСКВА 2022

Исходные данные.

Таблица 1. Длины линий и расстояния между подстанциями.

L1, км	30
L2, км	60
L1ГР, км	0,8
L1РП, км	0,4
LТПР, км	3

Таблица 2. Заданные параметры нагрузок.

Потребитель	MS, кВА	n
2	290	4
3	400	3
4	450	6
5	380	8
6	950	3
7	1300	3
8	2800	3
9	2400	2
11	6000	2

Вероятностные взаимосвязи между нагрузками тяговой подстанции, РП1 и ГРП1:



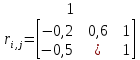
Таблица 3. Режимы напряжения на шинах 110 кВ ЭС1 и ЭС2 в % от U_ном

Часы суток	0-6	6-8	8-12	12-16	16-20	20-24
ЭС1	98	103	105	102	106	101
ЭС2	97	104	106	103	107	100

---

Рисунок 1. Схема системы электроснабжения.

1. Определение вероятностно-статистических характеристик нагрузок всех элементов системы электроснабжения 110-10 кВ, а также расчётных значений с заданной вероятностью их превышения γ=0,00135.

Пользуясь заданными значениями математического ожидания полной мощности и количеством трансформаторных подстанций, определим остальные вероятностно-статистические характеристики нагрузки для каждой из трансформаторных подстанций присоединения 2.

Математическое ожидание активной :



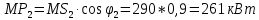
Математическое ожидание реактивной мощности:



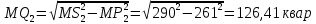
Для вычисления значений дисперсии активной, реактивной и полной мощности трансформаторных подстанций воспользуемся коэффициентом вариации:







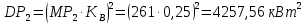
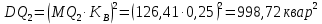
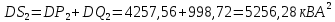
Далее определяется суммарная полная мощность всех трансформаторных подстанций присоединения 2 с заданной вероятностью превышения γ=0,00135.

Для этого необходимо вычислить суммарные значения математических ожиданий, дисперсий и среднеквадратичных отклонений активной, реактивной и полной мощности:



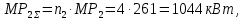
где n₂ – число трансформаторных подстанций в составе присоединения 2.

Аналогично для реактивной мощности имеем:



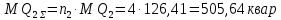
Значение суммарной полной мощности:



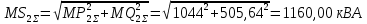
Аналогично для дисперсий:

---

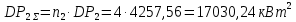
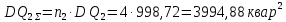
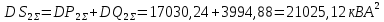
Среднеквадратичное отклонение для активной, реактивной и полной мощностей определяется по формуле:







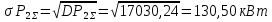
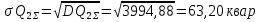
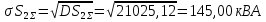
По правилу «трёх сигм» определяется полная мощность потребителя 2 для заданной вероятности превышения:



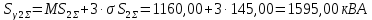
Расчёт для присоединений 3, 4, 5, 6, 7, 8 и 9 аналогичен данному. Результаты сведены в таблицу 4.

Далее определяются вероятностно-статистические характеристики нагрузки для секции шин 12.









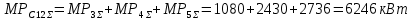
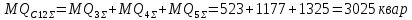
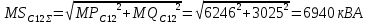
Дисперсии активной, реактивной и полной мощностей вычисляются по формулам:







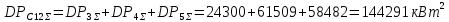
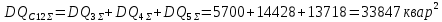
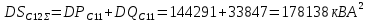
Определим значение среднеквадратичных отклонений мощностей секции 11:







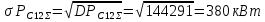
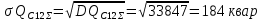
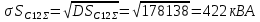
Тогда суммарная полная мощность нагрузки секции 11 с заданной вероятностью превышения определяется также по правилу трёх сигм:



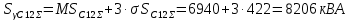
Вероятностно-статистические характеристики нагрузки для секций шин 9, 10, 11 рассчитываются аналогично. Результаты сведены в таблицу 4.

Суммарные вероятностно-статистические характеристики нагрузки распределительного пункта 1 рассчитываются аналогично. Результаты также отображены в таблице 4.

Суммарные характеристики нагрузок ГРП1 (С9+С10) и п/ст 2 (С7+С8) определяются аналогично. Результаты представлены в таблице 4.

Далее определяются вероятностно-статистические характеристики нагрузки секций 3, 4, 5 и 6 стороны НН подстанции 1. Характеристики нагрузки секций 4 и 6 уже получены, т. к. на этих секция присутствует только рассчитанные выше потребители (секция 9 ГРП1 для секции 4 и секция 10 ГРП1 для секции 6).

Математическое ожидание активной, реактивной и полной мощностей секции три определяется как сумма математических ожиданий соответствующих мощностей секций семь и одиннадцать:

---

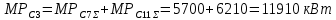
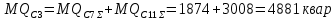
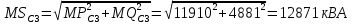
Для расчёта дисперсий необходимо воспользоваться коэффициентом корреляции, так как потребители РП1 и п/ст2 представляют собой разнородную нагрузку:











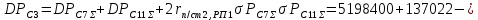
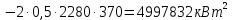
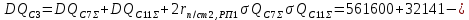
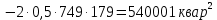
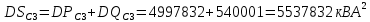
Среднеквадратичные отклонения мощностей определяются как корни из соответствующих дисперсий:







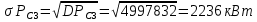
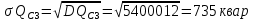
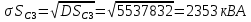
Расчётное значение полной мощности нагрузки секции 3 с заданной вероятностью превышения 0,00135:



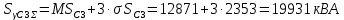
Расчёт для секций 4, 5 и 6 аналогичен. Результаты сведены в таблицу 5.

Теперь определим вероятностные характеристики нагрузки каждого из трансформаторов подстанции 1. Это попарные суммарные характеристики секций 3 и 4 и 5 и 6.







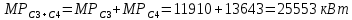
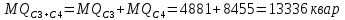
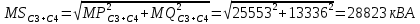
Для расчёта дисперсий необходимо учесть, что в нагрузке трансформатора, питающего секции 3 и 4, присутствуют три разнородных потребителя:










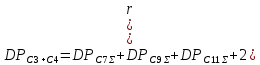
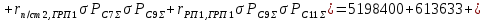
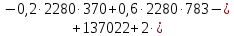
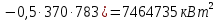
Расчёт дисперсии реактивной мощности аналогичен вышеприведённому. Остальные характеристики рассчитываются по формулам, использованным выше. Результаты сведены в таблицу 5.

---

Далее рассчитывается суммарная нагрузка подстанции 1. Расчёт производится также, как и в предыдущих случаях. Коэффициент корреляции не используется, так как он уже учтён в формулах для определения характеристик нагрузок трансформаторов. Результаты представлены в таблице 5.

Таблица 4. Вероятностно-статистические характеристики нагрузок.

№	n	MS	MP	MQ	DP	DQ	DS	MP	MQ	MS		DP		DQ		DS		P		Q		S		S
								ГРП 1 cos=			0,85		Kв=		0,15
6	3	950	808	500	14671	5635	20306	2423	1501	2850		44014		16905		60919		210		130		247		3590
8	3	2800	2380	1475	127449	48951	176400	7140	4425	8400		382347		146853		529200		618		383		727		10582
9	2	2400	2040	1264	93636	35964	129600	4080	2529	4800		187272		71928		259200		433		268		509		6327
C9								13643	8455	16050		613633		235686		849318		783		485		922		18815
7	3	1300	1105	685	27473	10552	38025	3315	2054	3900		82419		31656		114075		287		178		338		4913
8	3	2800	2380	1475	127449	48951	176400	7140	4425	8400		382347		146853		529200		618		383		727		10582
9	2	2400	2040	1264	93636	35964	129600	4080	2529	4800		187272		71928		259200		433		268		509		6327
10с								14535	9008	17100		652038		250437		902475		807		500		950		19950
9с+10с								28178	17463	33150		1265671		486123		1751793		1125		697		1324		37121
								РП 1 cos=			0,9		Kв=		0,25
2	4	290	261	126	4258	999	5256	1044	506	1160		17030		3995		21025		131		63		145		1595
4	6	450	405	196	10252	2405	12656	2430	1177	2700		61509		14428		75937		248		120		276		3527
5	8	380	342	166	7310	1715	9025	2736	1325	3040		58482		13718		72200		242		117		269		3846
C11								6210	3008	6900		137022		32141		169163		370		179		411		8134
3	3	400	360	174	8100	1900	10000	1080	523	1200		24300		5700		30000		156		76		173		1720
4	6	450	405	196	10252	2405	12656	2430	1177	2700		61509		14428		75937		248		120		276		3527
5	8	380	342	166	7310	1715	9025	2736	1325	3040		58482		13718		72200		242		117		269		3846
12с								6246	3025	6940		144291		33847		178138		380		184		422		8206
11с+12с								12456	6033	13840		281313		65988		347301		530		257		589		15608
								п/ст 2 cos=			0,95		Kв=		0,4
11	2	6000	5700	1874	5198400	561600	5760000	11400	3747	12000		10396800		1123201		11520001		3224		1060		3394		22182
7с								5700	1874	6000		5198400		561600		5760000		2280		749		2400		13200
8с								5700	1874	6000		5198400		561600		5760000		2280		749		2400		13200

---

Смотрите также файлы

• Греческий овощной суп "Фасолада".docx

• Отчет по лабораторной работе Приёмы оказания первой помощи пострадавшему.docx

• Реализация алгоритмов поиска по тексту.docx

• Контрольная работа дисциплина Налоговое право Ф. И. О студента Трущенкова Кристина Олеговна.docx

• 1. Теория государства и права Предмет, метод и функции теории государства и права.docx