ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 239
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Последняя графа таблицы содержит информацию об изменениях индивидуальных индексов цен или их приростах. С учетом этих приростов несложно определить первоначальные значения индексов, которые по товарам А, Б и В соответственно составляют 0,987, 1,042 и 1,025.
Рассчитаем значение сводного индекса:

Произведенный расчет позволяет заключить, что цены по данной товарной группе в среднем возросли на 1,9 %. Мы получили значение сводного индекса цен в среднегармонической форме, соответствующее сводному индексу Пааше.
Для получения значения, соответствующего индексу Ласпейреса, сводный индекс цен необходимо представить в среднеарифметической форме. При этом используется следующая замена:
С учетом этой замены сводный индекс цен в среднеарифметической форме можно представить следующим образом:
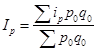 (109)
(109)Среднеарифметическая форма также может использоваться при расчете сводного индекса физического объема товарооборота. При этом производится замена:
Сводный индекс физического объема товарооборота в форме средней арифметической имеет вид:
 (110)
(110)Пример. Рассчитаем сводный индекс физического объема реализации продукции по данным о стоимости трех товаров товарной группы (табл. 71):
Таблица 71.
Реализация товаров А, Б, В в натуральном и стоимостном выражении
| Товар | Стоимостный объем реализации в базисном периоде, руб. | Изменение физического объема реализации в текущем периоде по сравнению с базисным, % |
| А | 87000 | +3,4 |
| Б | 54000 | -12,0 |
| В | 73000 | -8,5 |
Индивидуальные индексы физического объема, соответственно, будут равны 1,034, 0,880 и 0,915. С учетом этого рассчитаем среднеарифметический индекс:
В результате расчета мы получили, что физический объем реализации товаров рассматриваемой товарной группы в среднем снизился на 4,5 %.
Вопрос 5. Индексный анализ влияния структурных изменений.
Индексы позволяют оценить динамику показателей, характеризующих разнородные в качественном отношении совокупности, как правило, товарные группы. Однако даже если рассматривать данные по каждому товару отдельно или данные о производстве продукции одного вида, на величине результативного показателя будет отражаться влияние структурных изменений, например, изменений в структуре производства или реализации данного товара по территориям. Рассмотрим случай, когда один товар или вид продукции реализуется или производится в нескольких местах (табл. 72).
Таблица 72.
Данные о ценах и объемах реализации товара «X» в регионах
| Регион | 2011 | 2012 | |||
| цена, тыс. руб. | продано, шт. | цена, тыс. руб. | продано, шт. | ||
| 1 | 7 | 36000 | 8 | 10000 | |
| 2 | 5 | 12000 | 6 | 34000 | |
Проведем анализ изменения цен на данный товар. Из таблицы видно, что цена в каждом регионе возросла. Для сводной оценки этого роста воспользуемся средними показателями. Так как в данном случае реализуется один и тот же товар, вполне правомерно рассчитать его среднюю цену за 2011 и за 2012 гг.
Индекс цен переменного состава представляет собой соотношение средних значений за два рассматриваемые периода:

(111)
Рассчитанное значение индекса указывает на снижение средней цены данного товара на 0,8 %, т.е. с 6,50 до 6,45 тыс. руб. В то же время из приведенной выше таблицы видно, что цена в каждом регионе в 2012 г. по сравнению с 2011 г. возросла. Данное несоответствие объясняется влиянием изменения структуры реализации товаров по регионам: в 2011 г. по более высокой цене 7 тыс. руб. продали товара втрое больше, чем по цене 5 тыс. руб., а в 2012 г. ситуация принципиально изменилась. Иными словами, на динамике средней цены данного товара отразились структурные сдвиги в рассматриваемой совокупности. Оценить воздействие этого фактора можно с помощью индекса структурных сдвигов:
 (112)
(112)Первая формула в этом индексе позволяет ответить на вопрос, какой была бы средняя цена в 2012 г., если бы цены в каждом регионе сохранились на уровне 2011 г. Вторая часть формулы отражает фактическую среднюю цену 2011 г. В целом по значению индекса мы можем сделать вывод, что за счет структурных сдвигов цены снизились в среднем на 16,1 % (83,9 – 100 = -16,1 %).
Последним в данной системе является индекс цен фиксированного состава, который не учитывает влияние структуры и рассчитывается по уже известной нам формуле сводного индекса цен по методу Пааше:

Полученное значение индекса позволяет сделать вывод о том, что если бы структура реализации товара Х по регионам не изменилась, средняя цена возросла бы на 18,3 %. Однако влияние на среднюю цену фактора структурных изменений оказалось сильнее, и в итоге цена даже несколько снизилась. Данное взаимодействие рассматриваемых факторов отражается в следующей взаимосвязи:
1,183 * 0,839 = 0,992
Аналогично строятся индексы структурных сдвигов, переменного и фиксированного состава для анализа изменения себестоимости
, урожайности и других показателей.
Вопросы для самопроверки:
1. Что характеризует экономический индекс?
2. Чем отличается индивидуальный индекс от сводного индекса?
3. В каких единицах измерения выражаются индексы?
4. Что показывает разность между числителем и знаменателем сводного индекса цен? Как интерпретируется ее отрицательное значение?
5. При помощи какого показателя можно оценить снижение издержек производства, вызванное изменением себестоимости единиц выпускаемой продукции?
6. Что представляет собой индекс в форме средней?
7. Можно ли рассчитать сводный индекс переменного состава, зная средние цены реализации товаров за два квартала?
8. Что оценивает индекс структурных сдвигов?
9. Что характеризует индекс фиксированного состава?
Литература по теме:
Основная литература:
1. Улитина Е.В. Статистика: учебное пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия).
Дополнительная литература:
1. Общая теория статистики: статистическая методология в изучении коммерческой деятельности: учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2004.
2. Практикум по теории статистики: учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
3. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004.
4. Четыркин Е.М. Финансовая математика. – М.: Дело Лтд, 2006.
5. Методологические положения по статистике. – М.: Госкомстат России, 2010.
Практические задания.
Задание 1.
По данным о себестоимости и объемах производства продукции промышленного предприятия определите:
а) сводный индекс себестоимости;
б) сводный индекс физического объема продукции;
в) сводный индекс затрат на производство;
г) покажите взаимосвязь сводных индексов.
| Изделие | 2011 | 2012 | Расчетные графы | ||||
| себесто-имость единицы продукции, руб. | произ-ведено тыс. шт. | себесто-имость единицы продукции, руб. | произ-ведено тыс. шт. | | | | |
| А | 220 | 63,4 | 247 | 52,7 | | | |
| Б | 183 | 41,0 | 215 | 38,8 | | | |
| В | 67 | 89,2 | 70 | 91,0 | | | |
| Итого | | | | | | | |
Задание 2.
Определите общее изменение себестоимости продукции промышленного предприятия в 2012 г. по сравнению с 2011 г. и обусловленный этим изменением размер экономии или дополнительных затрат предприятия по следующим данным.
| Изделие | Общие затраты на производство в 2012 г., тыс. руб. | Изменение себестоимости изделия в 2012 г. по сравнению с 2011 г., % | Расчетные графы | |
| | | |||
| Электромясорубка | 1234 | +6,0 | | |
| Кухонный комбайн | 5877 | +8,4 | | |
| Миксер | 980 | +1,6 | | |
| Итого | | | | |
Задание 3.
По данным о строительно-производственной деятельности двух ДСК города рассчитайте:
а) индекс себестоимости переменного состава;
б) индекс себестоимости фиксированного составов;
в) индекс структурных сдвигов;
г) проверьте взаимосвязь индексов.
| Домостроительный комбинат | Построено жилья, тыс. м2 | Себестоимость 1 м2, тыс. руб. | Расчетные графы | |||||
| 2011 | 2012 | 2011 | 2012 | | | | ||
| ДСК-1 | 53 | 68 | 16,4 | 17,2 | | | | |
| ДСК-2 | 179 | 127 | 16,0 | 16,5 | | | | |
| Итого | | | | | | | | |
