При вычислении были использованы следующие правила дифференцирования: (x^a)' = ax^a-1
(a)' = 0,



Используем формулу:

Найдем производную первого члена, используя формулу из таблицы производных:



Производная от логарифма и под логарифмического выражения:



Найдем производную второго члена, используя формулы из таблицы производных и свойство сложной функции:



Производная от тригонометрической функции и производная с константой:



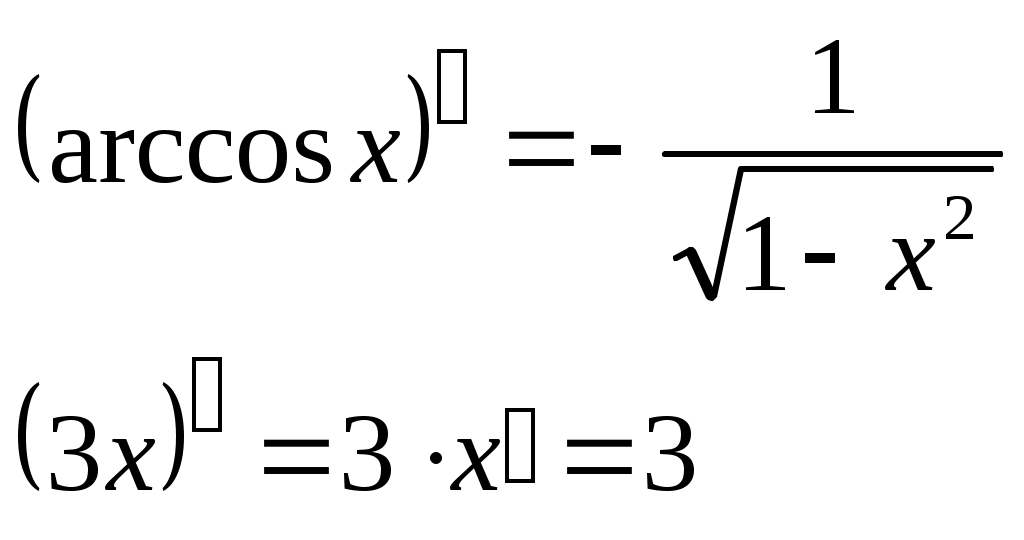
Результат:

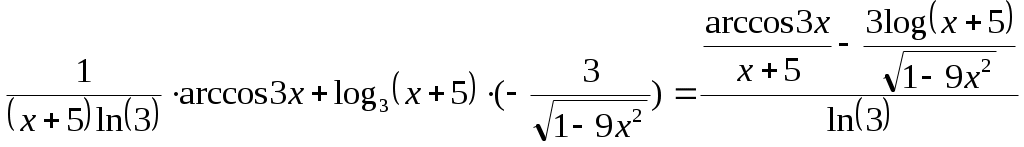
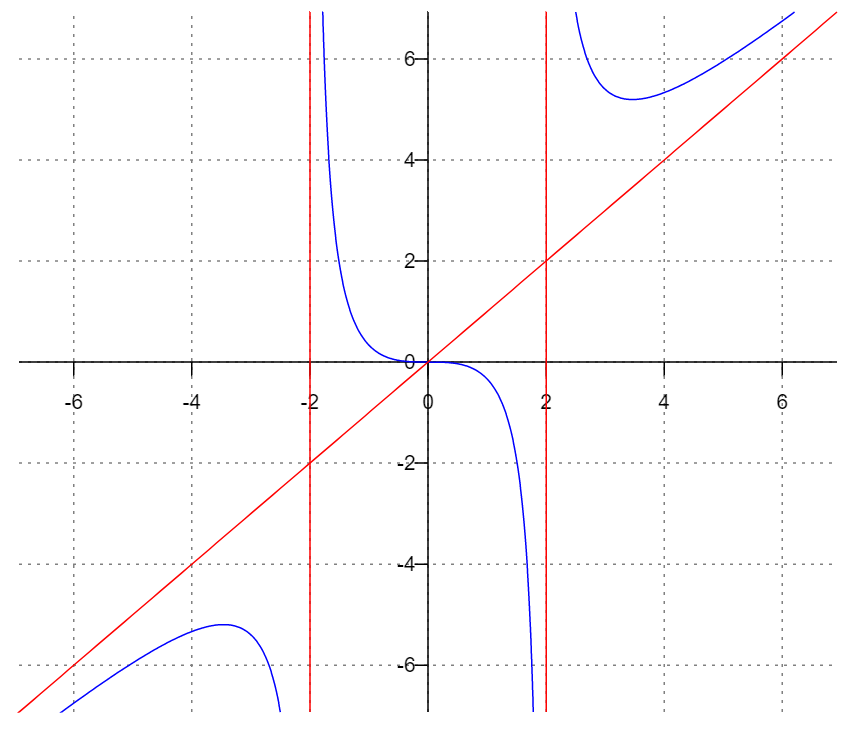
Задание 8.

 Вам предложена функция: 

Проведите исследование, согласно схеме:

1.    Найти область определения функции.

2.    Найти точки пересечения с осями.

3.    Исследовать функцию на четность/нечетность.

4.    Найти асимптоты.

5.    Найти экстремумы и интервалы монотонности функции.

6.    Найти интервалы выпуклости функции и точки перегиба.

7.    Найти дополнительные точки, уточняющие график.

8.    Построить график.

 Решение:

1. 
   Найти область определения функции.
   

Точки разрыва:



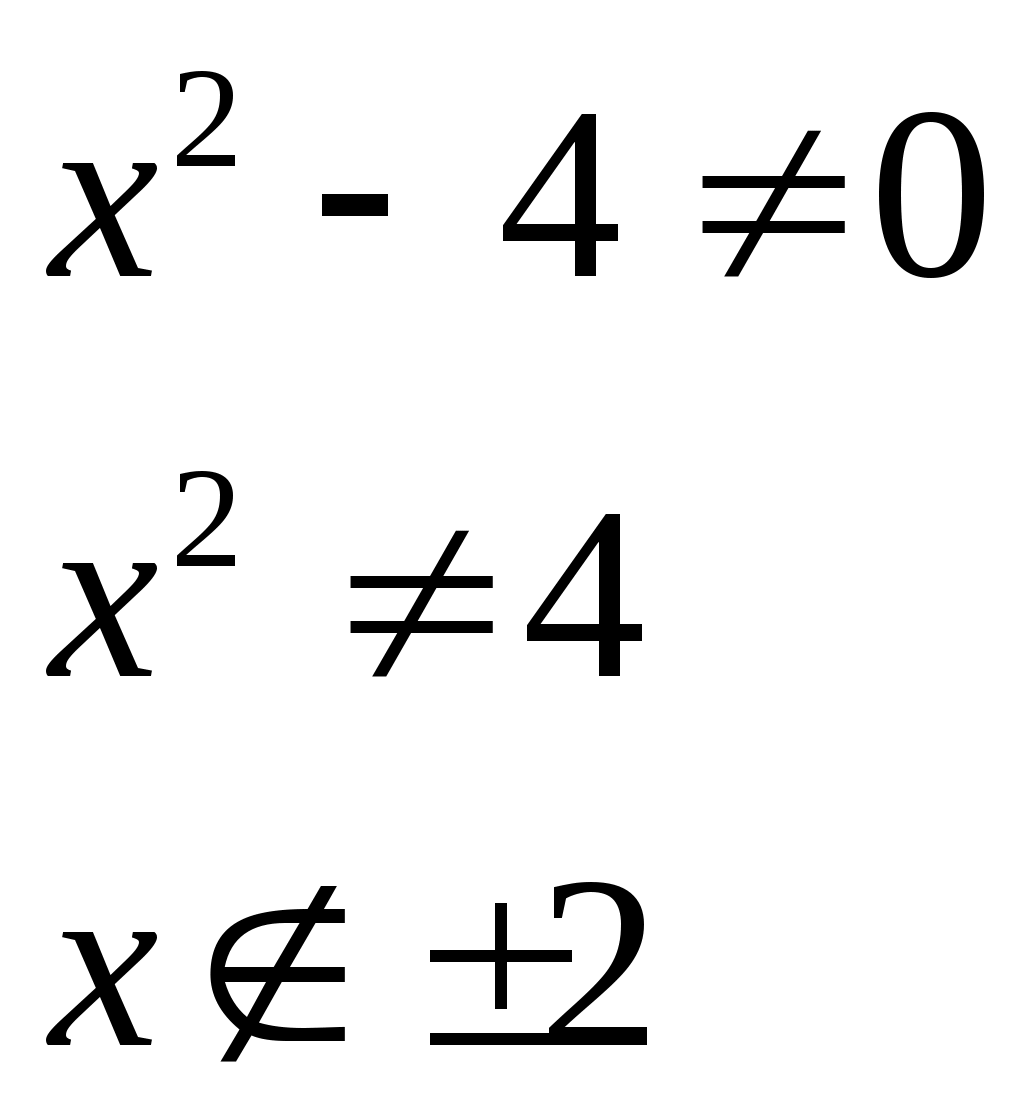
Значит, область определения функции:

∞;-4) (-4;4)

---

(4;+∞)

2. 
   Найти точки пересечения с осями. Приравняем к нулю.
   

Пересечение с осью 0Y: x=0, y=0

Пересечение с осью 0X:

y=0, тогда , х=0

3. 
   Исследовать функцию на четность/нечетность:
   

y(-x) = -y(x), нечетная функция

4. 
   Найти асимптоты:
   

Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:



Находим коэффициент k:





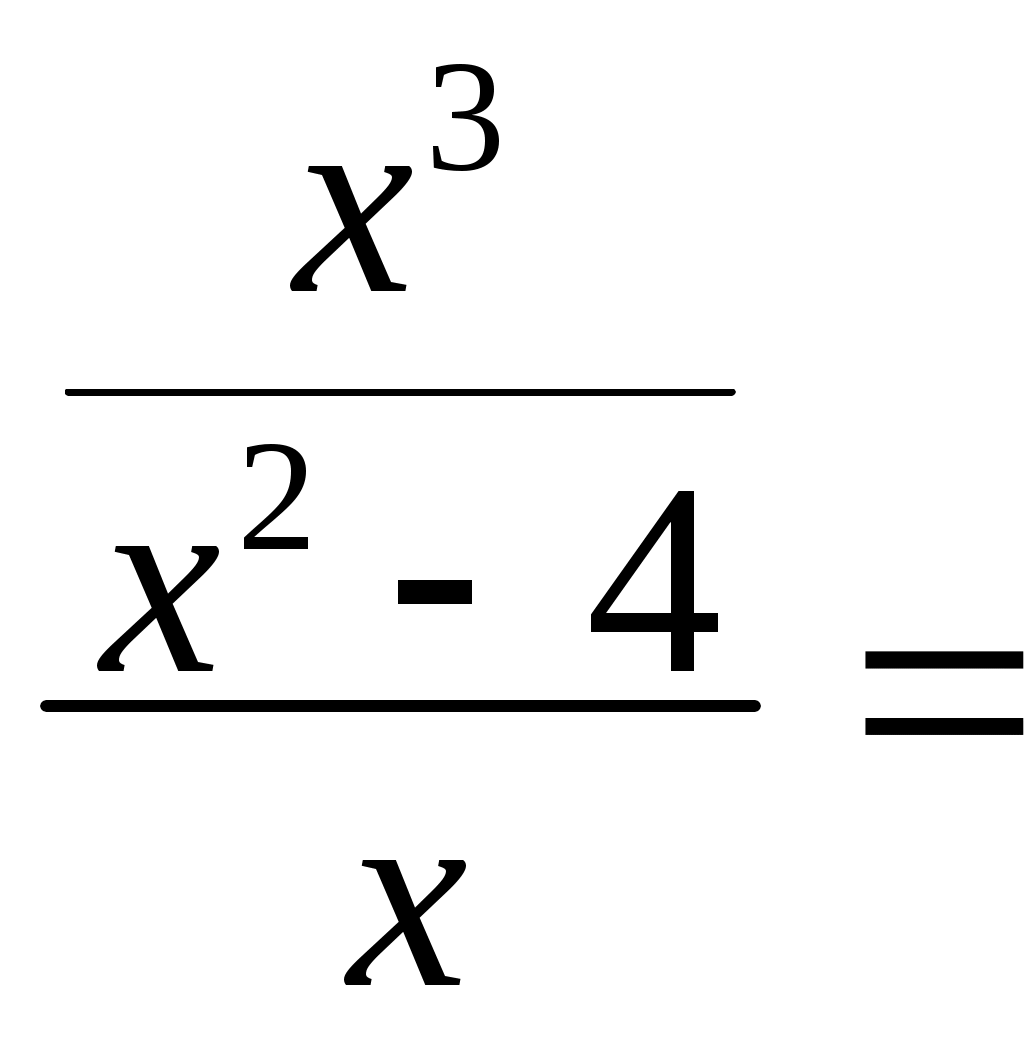
Находим коэффициент b:





Получаем уравнение наклонной асимптоты:

y = x
Найдем вертикальные асимптоты. Для этого определим точки разрыва:

x₁ = -2, x₂ = 2
Находим переделы в точке x=-2





x₁ = -2 - точка разрыва II рода и является вертикальной асимптотой.

---

Находим переделы в точке x=2





x₂ = 2 - точка разрыва II рода и является вертикальной асимптотой.

Найдем наклонную асимптоту при x → -∞:



Находим коэффициент k:





Находим коэффициент b:





Получаем уравнение наклонной асимптоты:

y = x

5. 
   Найти y = x^3/(x^2-4)
   Найдем точки разрыва функции: x₁ = 2, x₂ = -2
   Поскольку f(-x)=-f(x), то функция является нечетной. экстремумы и интервалы монотонности функции:
   

1. 
   Находим интервалы возрастания и убывания. Первая производная.
   

Находим нули функции. Для этого приравниваем производную к нулю

---

x²·(x²-12) = 0

или


x₁ = 0,

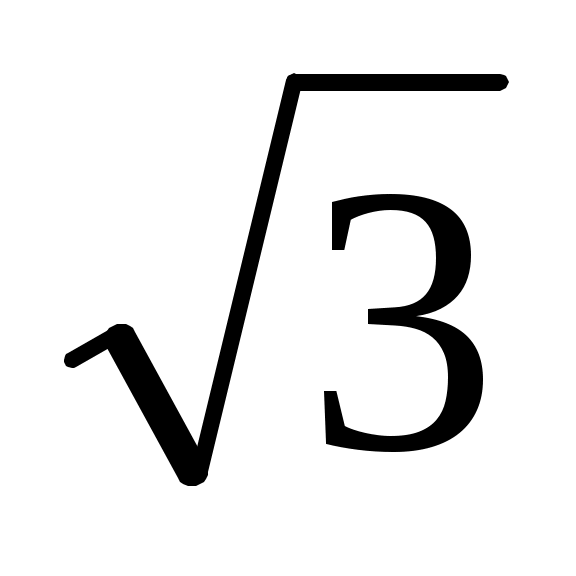(-∞;-2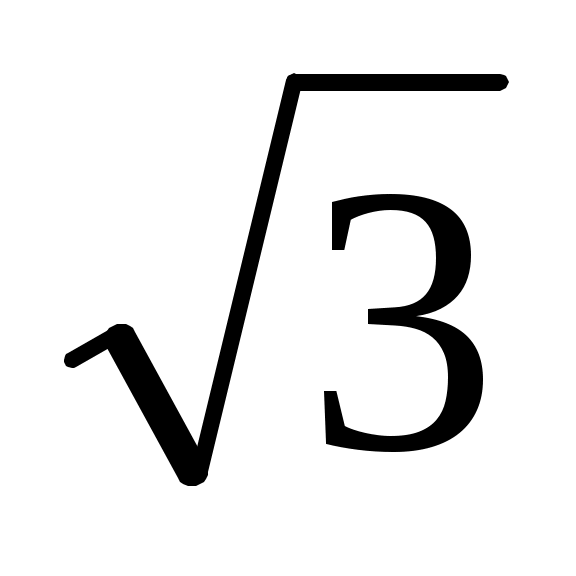 )	(-2 ;-2)	(-2;0)	(0;2)	(2;2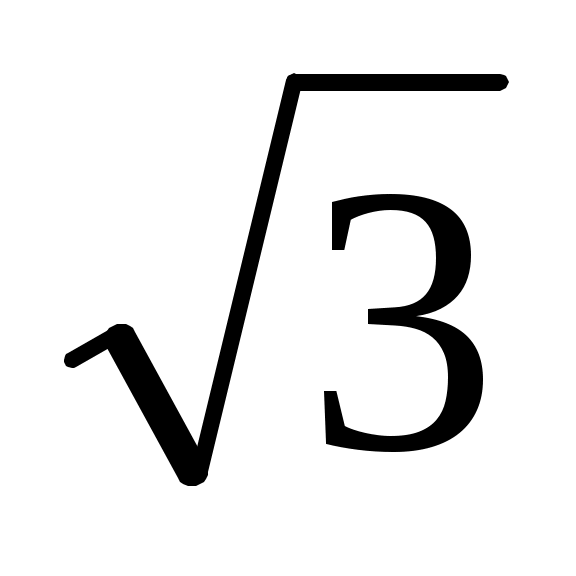 )	(2 ;+∞)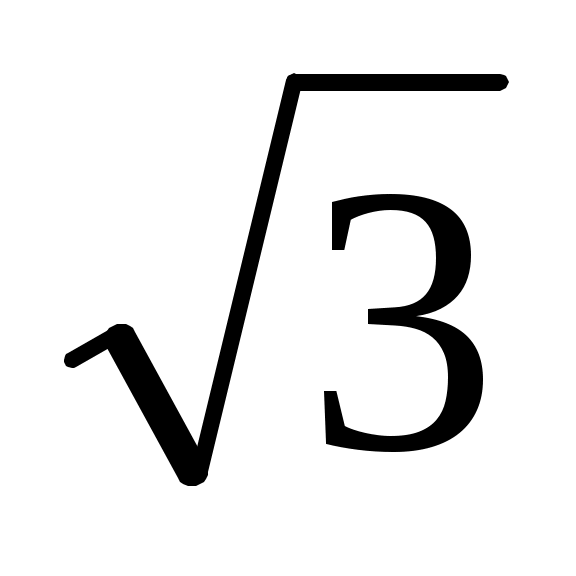
f'(x)> 0	f'(x) <0	f'(x) <0	f'(x) <0	f'(x) <0	f'(x)> 0
функция возрастает	функция убывает	функция убывает	функция убывает	функция убывает	функция возрастает

В окрестности точки x = -2 производная функции меняет знак с (+) на (-). Следовательно, точка x = -2 - точка максимума. В окрестности точки x = 2 производная функции меняет знак с (-) на (+). Следовательно, точка x = 2 - точка минимума.

2. 
   Найдем интервалы выпуклости и вогнутости функции. Вторая производная.
   

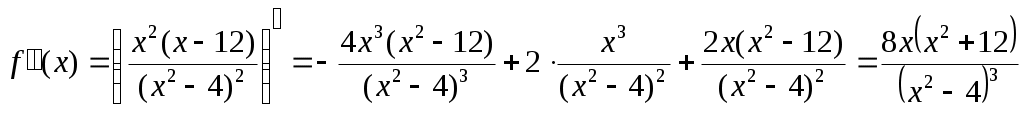
Находим корни уравнения. Для этого полученную функцию приравняем к нулю.

=> точки перегиба: x₁ = 0

(-∞ ;-2)	(-2; 0)	(0; 2)	(2; +∞)
f''(x) <0	f''(x)> 0	f''(x) <0	f''(x)> 0
функция выпукла	функция вогнута	функция выпукла	функция вогнута

---

6. 
   Найти дополнительные точки, уточняющие график:
   

7. 
   Построить график.
   

---

Смотрите также файлы

• Контрольная работа Вариант 4 Исполнитель Владимир Владимирович Романюта Студент Группы идо зб югп21 св.docx

• Публичноправовой статус адвокатуры в России.docx

• Задача 1. Какие из перечисленных субъектов являются органами исполнительной власти а департамент потребительского рынке областной администрации.docx

• Ответы на вопросы (для физических лиц) Обновление 19. 04. 2022 г.pdf

• Выполнение практических заданий по дисциплине земельное право (часть 11).docx