МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Российский экономический университет имени Г. В. Плеханова» К Р А С Н О Д А Р С К И Й Ф И Л И А Л К р а с н о д а р с к и й ф и л и а л Р Э У и м. Г. В. П л е х а н о в а

Факультет: «Экономика»

Профиль «Экономика предприятий и организаций»
дисциплина

«ЭКОНОМЕТРИКА»

Контрольная работа

Вариант 4
Выполнила:

Студент (ка)

группы 20-ФЭМТс-1Ф

Эктова Алина Валерьевна

Преподаватель:

…

Краснодар

2021

Задача 1.

Руководство торгового предприятия изучает статистические данные об объемах продаж холодильников (П₁, П₂…, шт.) в зависимости от их цены (Ц₁, Ц₂…, тыс.руб.).

Требуется выполнить следующие действия.

1. 
   Представить полученные данные на координатной плоскости в виде поля корреляции.
   
2. 
   Вычислить коэффициент корреляции между рядами данных по ценам и объемам продаж и сделать вывод.
   
3. 
   Вычислить коэффициенты линейной парной регрессии, представляющей зависимость объема продаж от цены.
   
4. 
   Построить график регрессии на поле корреляции.
   
5. 
   Вычислить среднюю относительную ошибку аппроксимации и сделать вывод.
   
6. 
   Вычислить коэффициент детерминации и сделать вывод.
   
7. 
   Дать точечный прогноз объема продаж по цене, сниженной на 10% от минимальной цены.
   
8. 
   Сопоставить доход, который дает продажа по минимальной цене, и прогноз дохода по сниженной цене. Сделать вывод о целесообразности снижения цены.
   
9. 
   С использованием F-критерия Фишера провести анализ статистической значимости уравнения регрессии при уровне значимости 5%.
   
10. 
    Дать интервальный прогноз объема продаж по цене, составляющей 105% от максимальной цены, с доверительной вероятностью 0,90.
    

---

Вариант 4

Номер варианта к/р	Цена товара					Объем продаж
	Ц1	Ц2	Ц3	Ц4	Ц5	П1	П2	П3	П4	П5
04.	10,43	13,07	17,56	22,21	26,93	194	86	62	51	37

Теоретическое значение F-статистики (F_теор) для указанных исходных данных равно 10,128.

Теоретическое значение t-статистики (t_теор) для указанных исходных данных равно 2,353.

Решение:

Руководство торгового предприятия изучает статистические данные об объемах продаж холодильников (П₁, П₂…, шт.) в зависимости от их цены (Ц₁, Ц₂…, тыс.руб.).

Цена холодильника (Х, шт.) и объема продаж холодильников (Y, тыс. руб.) в пяти торговых предприятиях, характеризуются следующими данными (таблица 1).

Таблица1

Объема продаж	у	194	86	62	51	37
Цена	х	10,43	13,07	17,56	22,21	26,93

Исследовать зависимость объема продаж холодильников от цены холодильника, используя линейную зависимость.

1. Построим поле корреляции (рис.1).



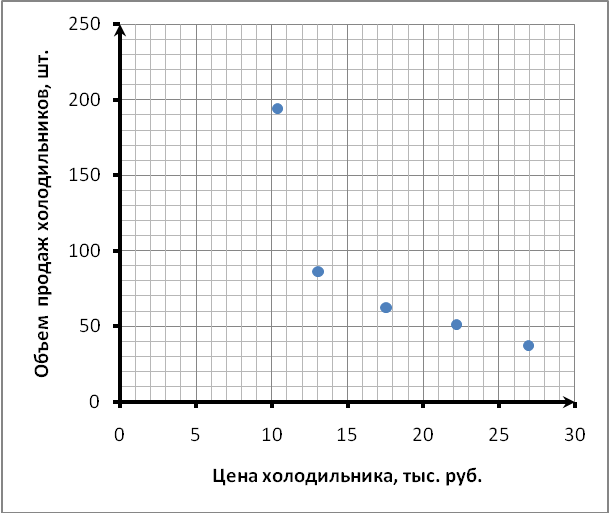
Рис. 1 Поле корреляции

2. Тесноту линейной связи между изучаемыми показателями оценит коэффициент корреляции r_xy и детерминации R². Для расчета r_xyи R² вычислим дисперсии факторов х

---

, у:

Величина дисперсии факторовx,y для наших данных:

Коэффициент корреляции r_xyустанавливает количественную меру тесноты связи и формирует качественную характеристику силы связи:



Коэффициент корреляции по шкале Чеддока связь между изучаемыми факторами высокая.

3. Для расчета параметров уравнения линейной регрессии построим расчетную таблицу (Таблица 2).

Таблица 2

	y	х	x*y	y2	x2			Ai
1	10,43	194	2023,42	37636	108,78	145,089	48,911	25,21%
2	13,07	86	1124,02	7396	170,82	124,590	-38,590	44,87%
3	17,56	62	1088,72	3844	308,35	89,727	-27,727	44,72%
4	22,21	51	1132,71	2601	493,28	53,622	-2,622	5,14%
5	26,93	37	996,41	1369	725,22	16,973	20,027	54,13%
Итого	90,2	430	6365,28	52846	1806,47	430	-	174,07%
Среднее значение	18,04	86	1273,056	10569,2	361,29	86	-	34,81%
	5,987727	56,33116	-	-	-	-	-	-
	35,85288	3173,2	-	-	-	-	-	-

---

Коэффициенты уравнения регрессии определим по формулам:

, .

Используя данные расчетной таблицы (Таблица 2), получим значение коэффициентов a, b уравнения регрессии:



.

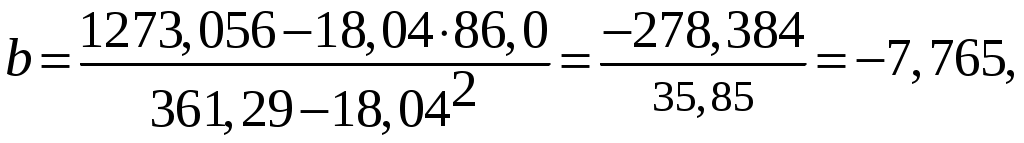
Таким образом, уравнение регрессии имеет вид: .

Экономический анализ решения регрессии показывает, что с увеличением цены холодильника на 1 тыс.руб., объем продаж холодильников снижается в среднем на 8 шт.

4. Построить линию регрессии на поле корреляции:



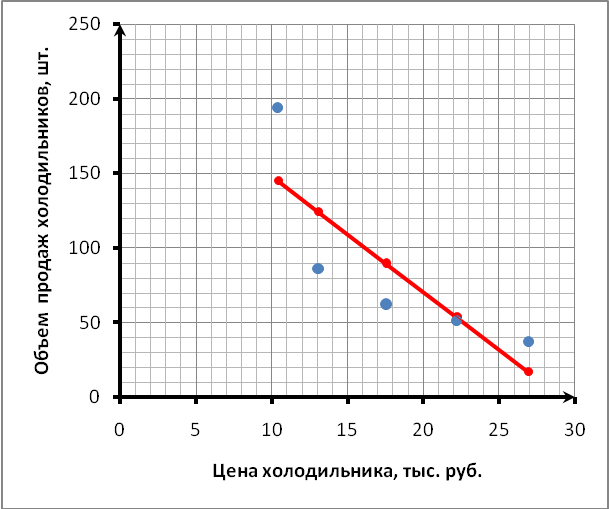
5. Вычислим значения по полученному уравнению регрессии:

	10,43	13,07	17,56	22,21	26,93
	145,089	124,590	89,727	53,622	16,973

Найдем среднюю ошибку аппроксимации, которая определяет качество полученной модели. Для расчета используются формулы:

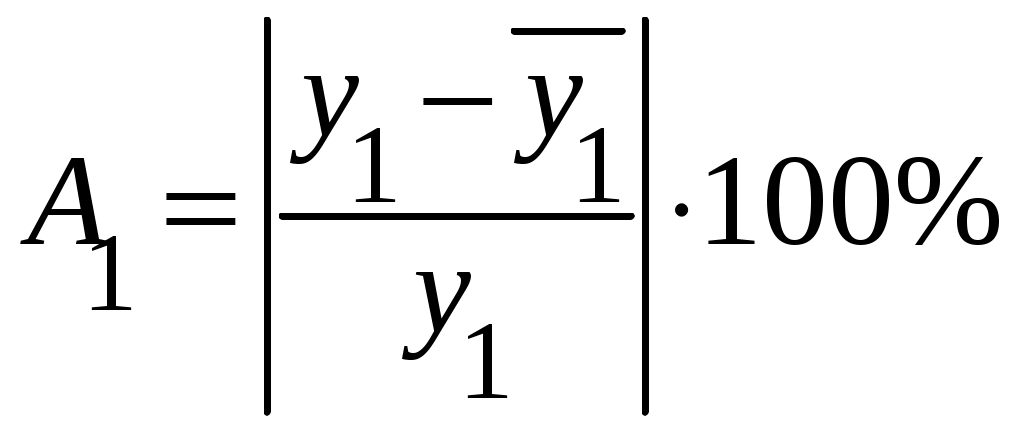и

Например, для первой строки данных таблицы имеем:



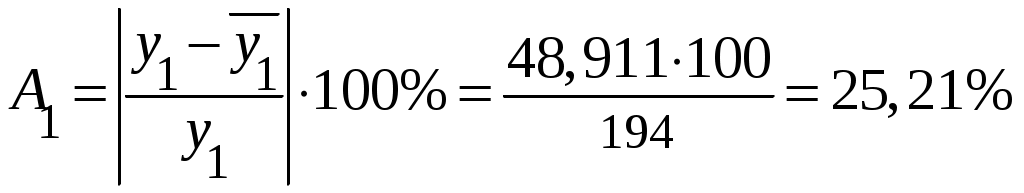
Аналогично найдем значения для всех строк . В результате получаем величину ошибки аппроксимации для нашей задачи:

---

где

Качество построенной модели оценивается как удовлетворительное, так как фактическое значение превышает 8-10%.

5. Найдем коэффициент детерминации:



Экономический смысл этого означает, что 68% вариации объема продаж холодильников(y) объясняется вариацией фактора цена холодильника (х).

Оценку статистической значимости уравнения регрессии в целом проведем с помощью F-критерия Фишера.

Фактическое значение F -критерия Фишера сравнивается с табличным значением F_табл(a ; k₁; k₂) при уровне значимости α и степенях свободы k₁= m и k₂= n - m -1. При этом, если фактическое значение F – критерия больше табличного, то признается статистическая значимость уравнения в целом.

Табличное значение критерия при и степенях свободы k₁=1 и k₂=5 - 2 =3 составляет F_табл= 10,128. Для расчета фактического значения F-критерия Фишера используем формулу:

.

Сравниваем полученное значение с табличным:

F_факт=6,41< F_табл= 10,128.

Так как, полученное (фактическое) значение меньше табличного, то уравнение регрессии признается статистически не значимым и не может использоваться для прогноза премиального фонда.

Оценку статистической значимости параметров регрессии проведем с помощью t -статистики Стьюдента.

Табличное значение t-критерия для числа степеней свободы df = n - 2 =5 - 2 =3 и уровня значимости a = 0,05 составит t_табл= 3,18.

Определим случайные ошибки параметров m_a, m_b и коэффициента корреляции по формулам:

---

Смотрите также файлы

• Склонение имен существительных.docx

• .docx

• Программа среднего профессионального образования 44. 02. 02 Преподавание в начальных классах Дисциплина Иностранный язык Практическое занятие 5.rtf

• Контрольная работа по философии на тему Философия Просвещения и её основные представители.docx

• Учебное пособие общие вопросы методики преподавания математики в начальной школе.pdf