Файл: Лабораторная работа по теме Изучение законов вращательного движения по дисциплине Физика.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.05.2024
Просмотров: 9
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство транспорта Российской Федерации
Федеральное агентство железнодорожного транспорта
Филиал Самарского государственного университета путей сообщения в г. Нижнем Новгороде
Факультет Высшего образования
Кафедра «Общеобразовательные и профессиональные дисциплины»
Лабораторная работа
по теме «Изучение законов вращательного движения»
по дисциплине «Физика»
Выполнил студент 1 курса
Шифр: 22141-ЭЖД-151
Кокорина А.М.
Проверил: Красильников В.С.
Н. Новгород 2022 год
Цель работы: изучение законов вращательного движения, применение закона сохранения энергии для поступательного и вращательного движений тел; измерение момента инерции маятника Обербека.
Приборы и принадлежности: прибор, состоящий из шкива, четырёх стержней и четырёх грузов (маятник Обербека), масштабная линейка, штангенциркуль, секундомер, шнурок с грузом.
Теоретическое введение
Момент инерции J материальной точки относительно какой – либо оси называется произведение массы m этой точки на квадрат её расстояния r до оси:
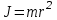 (1)
(1)Момент инерции тела относительно какой – либо оси равен сумме моментов инерции всех материальных точек тела относительно этой оси:
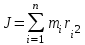 (2)
(2)Для тела, плотность которого распределена по объёму ρ = ρ(V), момент инерции вычисляется интегрированием по объему тела:
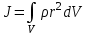 , (3)
, (3)где dV – элемент объема.
Момент инерции является физической величиной, характеризующей инертность тела при изменении им угловой скорости под действием вращающего момента.
Основной закон динамики вращательного движения твердого тела запишется так:
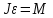 , (4)
, (4)где M – суммарный вращающий момент (векторная сумма всех моментов сил, действующих на тело), J – момент инерции тела, ε – угловое ускорение.
Этот закон можно записать и в другом виде:
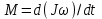 . (5)
. (5)Вращающий момент равен скорости изменения момента импульса тела, к которому приложен этот вращающий момент.
Вектор Jω называется моментом количества движения или моментом импульса тела.
Если точка, вращается по окружности с линейной скоростью v = ωr, то момент импульса точки Jω = mr2v/r = mvr.
Вращающееся тело обладает кинетической энергией вращательного движения:
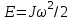 (6)
(6)Если сопоставить законы поступательного и вращательного движения, то легко видеть, что момент инерции во вращательном движении выполняет роль массы в поступательном движении, а момент силы – роль силы. Как масса тела характеризует инертность тела в поступательном движении, так момент инерции характеризует инертность тела во вращательном движении.
Т
 еория метода и описание установки. Законы вращательного движения можно изучать при помощи прибора, изображенного на рис. 1. Прибор состоит из шкива L радиуса r, закрепленного на оси O, четырёх стержней, расположенных под углом 90° друг к другу, и четырёх одинаковых цилиндрических грузов m, которые можно перемещать вдоль стержней и закреплять на определенном расстоянии от оси. Грузы закрепляются симметрично, т.е. так, чтобы центр тяжести совпадал с осью вращения. Прибор приводится во вращательное движение грузом P, прикрепленным к концу шнура, навитого на шкив. Груз P, удерживаемый на какой-то высоте h
еория метода и описание установки. Законы вращательного движения можно изучать при помощи прибора, изображенного на рис. 1. Прибор состоит из шкива L радиуса r, закрепленного на оси O, четырёх стержней, расположенных под углом 90° друг к другу, и четырёх одинаковых цилиндрических грузов m, которые можно перемещать вдоль стержней и закреплять на определенном расстоянии от оси. Грузы закрепляются симметрично, т.е. так, чтобы центр тяжести совпадал с осью вращения. Прибор приводится во вращательное движение грузом P, прикрепленным к концу шнура, навитого на шкив. Груз P, удерживаемый на какой-то высоте h
1 обладает потенциальной энергией m1gh, где m1 – масса груза.
Если предоставить возможность грузу P падать, то это падение будет происходить с ускорением a. При этом шкив со стержнем и расположенными на нём грузами будет вращаться с угловой скорость ω. При падении груза P потенциальная энергия m1gh перейдёт в кинетическую энергию поступательного движения груза m1v2/2 и кинетическую энергию вращательного движения прибора Jω2/2, где J – момент инерции прибора.
По закону сохранения энергии:
m1gh = m1v2/2 + Jω2/2, (7)
где v – скорость груза P в момент полного раскручивания шнура.
Сила, под действием которой груз m1 падает вниз,
F = P – T
где P – сила тяжести, T – сила натяжения шнура.
Отсюда
T = P – F
или
T = m1g – m1a = m1(g-a).
Сила T сообщает угловое ускорение вращающемуся телу. Момент этой силы:
M = Tr = m1(g-a)r, (8)
где r – радиус шкива.
Поступательное движение груза равноускоренное без начальной скорости, поэтому ускорение груза равно:
a = 2h/t2. (9)
Из формул (8), (4), (9) находим:
 (10)
(10)Для определения момента инерции нужно измерить опытным путем все величины, стоящие в правой части формулы (10); ускорение свободного падения g известно.
Измерения и обработка результатов измерения.
-
Измеряем штангенциркулем диаметр малого и большого шкивов r1 и r2. -
На технических весах определяется масса груза m1 (с точностью 0,1 г.) -
Наматываем на шкив нить, на конце которой прикреплён груз P так, чтобы он был на высоте h над началом отсчета. Масштабной линейкой измеряют h. -
Предоставив возможность грузу падать, по секундомеру определяют время падения груза.
По формулам (9), (8), линейное ускорение и вращающий момент, действующий на систему, далее вычисляют её угловое ускорение и момент инерции:
ε = a/r , J = M/ε .
Результаты измерений и вычислений заносят в таблицу.
| № опыта | r | h | t | a | M | ε | J | ΔJ |
| 1 | 0.3 | 1 | 5 | 0.08 | 1.85 | 0.27 | 6.86 | 10.48 |
| 2 | 1 | 11 | 0.02 | 1.86 | 0.07 | 26.57 | 9.23 | |
| 3 | 1 | 8 | 0.03 | 1.86 | 0.1 | 18.6 | 1.26 | |
| Среднее значение | x | x | x | x | 1.86 | 0.147 | 17.34 | 6.99 |
m1 = 0.635 кг.
r = 0.3 м.
h = 1 м.
t1 = 5 сек., t2 = 11 сек., t3 = 8 сек.
a1 = 2h/t12 = 0.08 м/сек2;
a2 = 2h/t22 = 0.02 м/сек2;
a3 = 2h/t32 = 0.03 м/сек2;
M1 = m1*(g – a1)*r = 0.635*9.72*0.3 = 1.85 кг*м2/сек2;
M2 = m2*(g – a2)*r = 0.635*9.78*0.3 = 1.86 кг*м2/сек2;
M3 = m3*(g – a3)*r = 0.635*9.77*0.3 = 1.86 кг*м2/сек2;
ε1 = a1/r = 0.08/0.3 = 0.27 сек-2;
ε2 = a2/r = 0.02/0.3 = 0.07 сек-2;
ε3 = a3/r = 0.03/0.3 = 0.1 сек-2;
J1 =
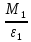 =
= 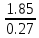 = 6.86 кг*м2;
= 6.86 кг*м2;J2 =
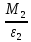 =
=  = 26.57 кг*м2;
= 26.57 кг*м2;J3 =
 =
= 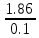 = 18.6 кг*м2;
= 18.6 кг*м2;Jср. = (J1 + J2 + J3)/3 = (6.86 + 26.57 + 18.6)/3 = 17.34 кг*м2;
ΔJ1 = |J1-Jср.| = 10.48 кг*м2;
ΔJ2 = |J2-Jср.| = 9.23 кг*м2; ΔJср. = ΔJ1 + ΔJ2 + ΔJ3 = 6.99 кг*м2;
ΔJ3 = |J3-Jср.| = 1.26 кг*м2;


