1. Типы переменных в эконометрических моделях.
По отношению к выбранной спецификации все экономические переменные объекта подразделяются на:

Эндогенные (зависимые) – экономические переменные, значения которых определяются (объясняются) внутри модели в результате взаимодействия соотношений, образующих модель.

Экзогенные (независимые) – экономические переменные, значения которых определяются вне данной модели.

* При наличии хотя бы одной экзогенной переменной модель называется открытой, в противном случае –

замкнутой.

Лаговые переменные – экзогенные или эндогенные переменные, датированные предыдущими моментами времени и находящиеся в уравнении с текущими переменными.

Предопределенные – переменные, выступающие в роли факторов-аргументов или объясняющих переменных (лаговые эндогенные, лаговые экзогенные, текущие экзогенные).
2. Спецификация парной линейной регрессионной модели, предпосылки Гаусса-Маркова.
Эконометрическая модель со спецификацией вида 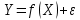, где Y – эндогенная (зависимая) переменная; Х – экзогенная (независимая) переменная (регрессор); 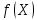– детерминированная составляющая эндогенной переменной (уравнение регрессии), полностью объясняемая значением экзогенной переменной; 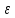- случайная составляющая эндогенной переменной (случайное возмущение), которая не может быть объяснена значением Х, называется регрессионной моделью. Она является парной, если эндогенная переменная зависит только от одного регрессора.

В модели парной линейной регрессии эту зависимость между переменными представляют в виде:



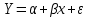
Например, 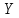- расходы фирмы, 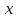- объем выпущенной продукции за месяц. Тогда 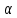- условно-постоянные расходы,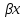

---

- условно-переменные расходы.

Относительно вектора случайных возмущений принимаются следующие предпосылки - условия Гаусса-Маркова:

1) Математическое ожидание вектора возмущений равно нулю (1 предпосылка), т.е. случайное возмущение в среднем не оказывает влияния на эндогенную переменную: .

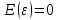2) Дисперсия возмущений не зависит от номера наблюдения (возмущение гомоскедастично -2 предпосылка):

.

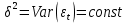3) Ковариация между значениями возмущений в различных наблюдениях равна 0 (возмущение не автокоррелировано – 3 предпосылка): .

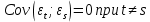4) Ковариация между регрессором и случайным возмущением равна 0 (4 предпосылка):

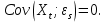
5) Возмущения имеют совместное нормальное распределение (5 предпосылка)
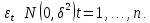
3. Теорема Гаусса - Маркова.
Если:

1) модель правильно специфицирована, т.е. зависимость вида 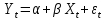действительно существует;

2) 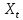являются детерминированными величинами и не равны между собой;

3) 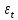– случайные величины, причем:

3. 1)

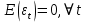
3. 2)

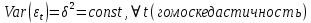
3. 3) C

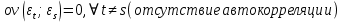
Тогда МНК оценки 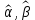являются:

• 
  линейными по Y
  
• 
  несмещенными
  
• 
  эффективными
  

оценками параметров 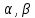, т. е. имеют наименьшую дисперсию (эффективны) в классе всех линейных несмещенных оценок.
4. Спецификация множественной линейной регрессионной модели в матричной форме.
Матричная форма





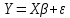
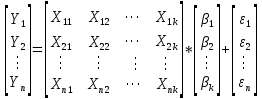
Обозначения:

• 
  n – число наблюдений;
  
• 
  k – число параметров;
  
• 
  матрица регрессоров Х – детерминированная полного ранга: rank(X)=k
  

---

* Первый столбец матрицы при наличии в спецификации свободного члена:



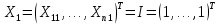
n,1
5. Оценка параметров множественной регрессионной модели методом наименьших квадратов в матричной форме.
Оценка параметров классической модели множественной линейной регрессии производится методом наименьших квадратов (МНК) и состоит в решении системы нормальных уравнений для множественной регрессии.

Критерий отбора:












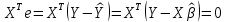
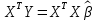
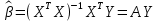
где 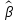– вектор оценок параметров модели; A – детерминированная матрица, определяемая через матрицу регрессоров. Одним из достоинств МНК является линейность МНК-оценок. Полученный результат подтверждает это свойство.
6. Основные числовые характеристики вектора оценок параметров классической множественной регрессионной модели.
Вектор оценок параметров модели 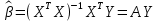– случайный вектор, его основными числовыми характеристиками являются:

1) вектор математических ожиданий



Оценка параметра называется несмещенной, если ее математическое ожидание равно значению параметра:

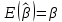
2) автоковариационная матрица:



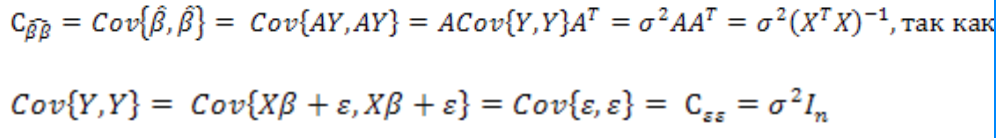
Оценка называется эффективной, если она имеет минимальную среднюю квадратическую ошибку:





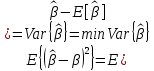
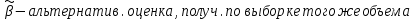
7. Основные числовые характеристики вектора остатков в классической множественной регрессионной модели.
1) Математическое ожидание:

---

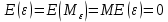
2) Автоковариационная матрица:


8. Основные числовые характеристики вектора возмущений в классической множественной регрессионной модели.
1) Математическое ожидание:

E { } = 0

2) Автоковариационная матрица:


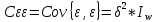
9. Основные числовые характеристики вектора значений эндогенной переменной в классической множественной регрессионной модели.
1) Математическое ожидание:



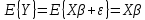
2) Автоковариационная матрица:




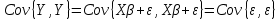
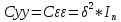
10. Основные числовые характеристики вектора оценок значений эндогенной переменной в классической множественной регрессионной модели.
1) Оценка вектора значений эндогенной переменной:



2) Математическое ожидание:



3) Автоковариационная матрица:


11. Основные числовые характеристики вектора прогнозов значений эндогенной переменной в классической множественной регрессионной модели.


12. Свойство несмещенности МНК- оценок параметров множественной регрессионной модели.
Для построения МНК-оценок параметров 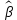  множественной регрессии по выборочным данным используется критерий отбора следующего вида


где 
-вектор столбец остатков множественной регрессии. Выразим ESS через вектор оценок параметров

---

Результат дифференциации критерия ESS по вектору-строке оценок параметра 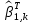дает необходимое условие экстремума:

Таким образом система нормальных уравнений в матричной форме принимает вид:

А вектор-столбец оценок параметров модели определяется линейным выражением

Вектор оценок параметров модели - случайный вектор, его основными количественными характеристиками являются: вектор математических ожиданий и матрица автоковариаций. Определим вектор математических ожиданий

Таким образом, МНК-оценки параметров множественной регрессии несмещенные, так как мат.ожидание оценки параметра равно истинному значению параметра.
13. Порядок оценивания линейной регрессионной модели в Excel при помощи функции ЛИНЕЙН.
Рассмотрим алгоритм оценивания парной линейной регрессии при помощи функции ЛИНЕЙН:

1) В свободном месте рабочего листа выделить область ячеек размером 5 строк и 2 столбца для вывода результатов;

2) В Мастере функций выбрать ЛИНЕЙН (категория «Статистические»);

3) Заполнить поля аргументов функции:

• 
  Известные_значения_y — адреса ячеек, содержащих значения признака;
  
• 
  Известные_значения_x — адреса ячеек, содержащих значения фактора;
  
• 
  Константа — значение (логическое), указывающее на наличие свободного члена в уравнении регрессии: если необходимо выполнить оценку двух параметров — постоянного и регрессионного, то в строку Конст следует внести 1;
  
• 
  Статистика — значение (логическое), которое указывает на то, следует ли выводить дополнительную информацию по регрессионному анализу или нет: так как при оценке параметров модели нас прежде всего интересуют статистические сведения, в окно строки Статистика следует внести 1;
  

---

Смотрите также файлы

• Краткое содержание курсовых работ тематика курсовых работ.pdf

• Тема Английская классическая школа (А. Смит, Д. Рикардо).docx

• Дисциплина Теоретические и методические основы взаимодействия воспитателя с родителями (лицами, их заменяющимися) и сотрудниками дошкольной образовательной организации Задание.docx

• ЗападноКазахстанский аграрнотехнический университет имени Жангир хана.doc

• Неоклассическая теория.docx