Определение критического значения F - статистики в Excel:

• 
  Категория — Статистические
  
• 
  Функция — Fраспобр; F.обр.ПХ
  

Параметры функции Fраспобр:

1. Вероятность (уровень значимости)

2. Число степеней свободы 1 (v1 =k-1)

3. Число степеней свободы 2 (v2 = n - k)

Третий шаг. Установление взаимосвязи между вспомогательной статистикой и коэффициентом детерминации



Вывод.

Проверка значимости F-статистики позволяет сделать вывод о значимости коэффициента детерминации, так как F= 0 при R^2=0

Если Fвыч  Fкр то нулевая гипотеза не отвергается
24. Тестирование значимости группы оценок параметров.
Для проверки статистической значимости некоторой части (группы) оценок параметров, т.е. о равенстве нулю не всех коэффициентов регрессии одновременно, используется F- статистика вида:

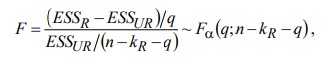(1)

где ESS_UR — сумма квадратов остатков «длинной» регрессии, включающей все регрессоры, ESS_R — сумма квадратов остатков «короткой» регрессии, включающей регрессоры на параметры которых не наложены ограничения нулевой гипотезы, k_R — число параметров короткой регрессии, k_UR = k_R + q — число параметров длинной регрессии, q = k_UR − k_R.

В случае, если на параметры всех регрессоров длинной регрессии, кроме свободного члена, наложены ограничения в рамках нулевой гипотезы статистика (1) принимает вид



С учетом того, что
25. Тестирование правильности составления спецификации: тест Рамсея.
Типичными ошибками спецификации модели являются следующие:

1. 
   Неверно выбран тип уравнения регрессии (например, вместо нелинейной функции использовалась линейная)
   
2. 
   В линейное уравнение множественной регрессии включен несущественный регрессор
   
3. 
   В линейное уравнение множественной регрессии не включен существенный регрессор
   

---

Для тестирования правильности выбора спецификации в эконометрических пакетах применяется тест RESET, предложенный Рамсеем в 1969 г.

Алгоритм теста состоит из следующих шагов.

1. 
   Оценивается спецификация исследуемой модели: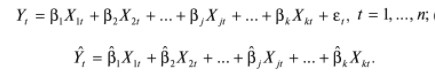
   
2. 
   Оценивается вспомогательная регрессия: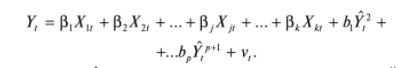
   

Нулевая гипотеза формулируется в рамках вспомогательной модели:



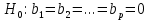
Нулевую гипотезу можно проверить при помощи F-теста:

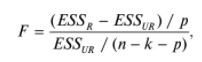(1)

Где 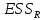- сумма квадратов остатков усеченной (исследуемой) регрессии; 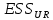- сумма квадратов остатков неусеченной (вспомогательной) регрессии.

Если вычисленное значение статистики окажется больше критического значения



Гипотеза 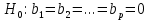отвергается, и спецификация модели признается неверной. F-статистики типа (1) имеют распределение Фишера только в случае, если случайные возмущения регрессионной модели являются независимыми и нормально распределенными.
26. Диагностика эконометрических моделей: тестирование гипотезы нормальности возмущений (тест Харке-Бера).
Одним из часто используемых тестов на нормальность случайных возмущений регрессионных моделей является тест Харке-Бера. Статистика теста основана на сравнении центральных нормированных моментов третьего (коэффициент ассиметрии) и четвертого (коэффициент островершинности) 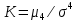порядков случайных возмущений исследуемой модели с соответствующими характеристиками нормального распределения, для которого, как известно, S=0, K=3 и имеет вид

---

(1)

Оценки характеристик, включенных в формулу, вычисляются через остатки регрессионной модели:



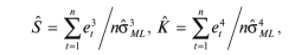
Где

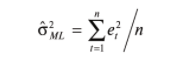- оценка дисперсии возмущений, полученная в рамках метода максимального правдоподобия.

Нулевая и альтернативные гипотезы теста Харке-Бера формулируются следующим образом:



Статистика (1) имеет распределение хи-квадрат с двумя степенями свободы, и если вычисленное значение больше критического, нулевая гипотеза о нормальном распределении возмущений регрессионной модели отвергается. Тест Харке-Бера является асимптотическим тестом, те применим к большим выборкам. Для малых выборок в эконометрических пакетах в формуле (1) сомножитель перед скобками заменен на n-k:



Где k- число оцениваемых параметров регрессионной модели.

27. Автокорреляция случайного возмущения: причины, последствия.

Автоковариационная матрица вектора случайных возмущений при наличии автокорреляции имеет следующую структуру:



Причинами автокорреляции являются:

• 
  Ошибки спецификации (пропуск важной объясняющей переменной, использование ошибочной функциональной зависимости между переменными)
  
• 
  Ошибки измерений
  
• 
  Характер наблюдений (например, данные временных рядов)
  

Последствия автокорреляции такие же, как и от гетероскедастичности. Вектор остатков регрессии 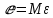при наличии автокорреляции возмущений имеет количественные характеристики


В этом случае

---

Что приводит к нарушению свойства несмещенности оценок дисперсии возмущения и автоковариационных матриц всех случайных векторов эконометрической модели.

28. Алгоритм теста Дарбина-Уотсона на наличие (отсутствие) автокорреляции случайных возмущений.
Тест Дарбина-Уотсона основан на предпосылках: случайное возмущение распределено нормально и не подвержено гетероскедастичности, модель не включает лаговые значения эндогенных переменных. Статистика теста вычисляется по формуле:



Где е- остатки регрессии, 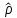- выборочный коэффициент корреляции между остатками регрессии, разделенными одним лагом.

Против нулевой гипотезы теста можно выбрать три альтернативные: 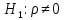(двусторонный тест) 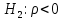(односторонний тест), (односторонний тест).


Последовательность его выполнения:

1. выполняется оценка параметров модели и вычисление остатков: , где

2. вычисление статистики DW (по формуле выше):

3.выбор табличных значений границ критического значения статистики: d_u, d_L( по параметрам n, K=k-1, α- для одностороннего теста, а/2 – для двустороннего теста);

4.определение интервала, в который попадает вычисленное значение статистики DW.



При этом возможны следующие случаи:

Наличие положительной автокорреляции: DWL.

Наличие отрицательной автокорреляции: DW >4-dL.

Автокорреляция отсутствует: dU≤ DW≤ 4-dU.

Зоны неопределенности: dL
Поскольку коэффициент корреляции принимает значения -1<=r<=1 то для значений статистики DW выполняется неравенство 0<=DW<=4.

1   2   3

---

29. Способы корректировки автокорреляции: алгоритм метода Кохрейна-Оркатта.

Пусть исходное уравнение регрессии   содержит автокорреляцию случайных членов.

Допустим, что автокорреляция подчиняется автокорреляционной схеме первого порядка:   , где   - коэффициент автокорреляции, а   - случайный член, удовлетворяющий предпосылкам МНК.

Данная схема оказывается авторегрессионой, поскольку   определяется значениями этой же величины с запаздыванием, и схемой первого порядка, потому что в этом случае запаздывание равно единице.

Величина   есть коэффициент корреляции между двумя соседними ошибками. Пусть  известно. Преобразуем исходное уравнение регрессии следующим образом:

 .

Алгоритм метода Кохрейна-Оркатта.

1. По выборочным данным выполняется настройка модели, и вычисляется вектор остатков регрессии е = (e₁, e₂ , …, e_n)^T.

2. По остаткам регрессии оценивается модель авторегрессии e_t=ρe_t-1+ v_t

3. С оценкой параметра авторегрессии выполняются этап преобразования переменных и определения МНК – оценок вектора параметра β.

4. Строится новый вектор остатков, и процедура повторяется, начиная с п. 2. Интеграционный процесс заканчивается при условии совпадения оценок по последней и предпоследней интерациях с заданной степенью точности.

30. Гетероскедастичность случайного возмущения: причины, последствия.

Гетероскедастичность - ситуация, когда дисперсия ошибки в уравнении регрессии изменяется от наблюдения к наблюдению. В этом случае приходится подвергать определенной модификации МНК (иначе возможны ошибочные выводы). Для обнаружения гетероскедастичности обычно используют 3 теста: тест ранговой корреляции Спирмена, тест Голдфеда-Квандта и тест Глейзера Доугерти.

Гетероскедастичность случайных возмущений – возмущения обладают различными дисперсиями r2i=r2wi, но не коррелированны друг с другом.

Причина: при гетероскедастичности распределение u для каждого наблюдения имеет нормальное распределение и нулевое ожидание, но дисперсия распределений различна.

Последствия нарушения условия гомоскедастичности случайных возмущений:

1. Потеря эффективности оценок коэффициентов регрессии, т.е. можно найти другие, отличные от Метода Наименьших Квадратов и более эффективные оценки

2. Смещенность стандартных ошибок коэффициентов в связи с некорректностью процедур их оценки

31. Алгоритм теста Голдфельда-Квандта на наличие (отсутствие) гетероскедастичности случайных возмущений.

Гипотеза(1): 

Шаг 1. Уравнения наблюдений объекта   следует упорядочить по возрастанию суммы модулей значений предопределенных переменных модели (2),

 



т.е. по возрастанию значений



Шаг 2. По первым   упорядоченным уравнениям наблюдений объекта вычислить МНК-оценки параметров модели и величину   где   - МНК-оценка случайного возмущения 

Шаг 3. По последним   упорядоченным уравнениям наблюдений вычислить МНК-оценки параметров модели и величину ESS, которую обозначим 

Шаг 4.Вычислить статистику   .

Шаг 5. Задаться уровнем значимости   и с помощью функции FРАСПОБР Excel при количествах степеней свободы   , где   определить (1-  -квантиль,   распределения Фишера.

Шаг 6. Принять гипотезу (1), если справедливы неравенства

 



Т.е. при справедливых неравенствах случайный остаток в модели (2) полагать гомоскедастичными. В противном случае гипотезу (1) отклонить как противоречащую реальным данным и сделать вывод о гетероскедастичности случайного остатка в модели (2).

32. Способы корректировки гетероскедастичности. Метод взвешенных наименьших квадратов.

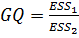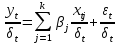Одним из основных способов корректировки гетероскедастичности является использование метода взвешенных наименьших квадратов. Он применяется в том случае, когда известны диагональные элементы автоковариационной матрицы   вектора возмущений  . В этом случае уравнения наблюдений можно преобразовать следующим образом. Поделим каждый член на СКО возмущения:  , где t=1….n. В результате преобразования спецификация принимает вид спецификации классической регрессионной модели:  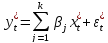 . Определим количественные характеристики случайного возмущения  :

математическое ожидание: E{ }=E{ }= =0

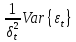дисперсия случайного члена: Var { }=Var{ }= = =1, таким образом 

N(0,1) и при помощи данного преобразования случайное возмущение приобрело свойство гомоскедастичности.

---

Смотрите также файлы

• Краткое содержание курсовых работ тематика курсовых работ.pdf

• Тема Английская классическая школа (А. Смит, Д. Рикардо).docx

• Дисциплина Теоретические и методические основы взаимодействия воспитателя с родителями (лицами, их заменяющимися) и сотрудниками дошкольной образовательной организации Задание.docx

• ЗападноКазахстанский аграрнотехнический университет имени Жангир хана.doc

• Неоклассическая теория.docx