МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение

высшего образования

«Тольяттинский государственный университет»

Архитектурно-строительный институт
Центр архитектурных, конструктивных решений и организации строительства

КОнтрольная работа
по учебному курсу «Геодезия 2»
Вариант 6

Студент	Ермолаев Тимур Артурович (И.О. Фамилия)
Группа	СТРбвд-2003д
Преподаватель	Грицкив Любовь Николаевна (И.О. Фамилия)

Тольятти 2022
Вариант №6

1. 
   Какие существуют способы детальной разбивки кривой? Какова сущность детальной разбивки кривой, способом прямоугольных координат? Ответ дополнить схемой.
   

Способ прямоугольных координат

Порядок разбивки данным способом следующий.

1)Задавшись длиной дуги S (расстояние между соседними точками разбивки), приняв нк или кк за начало координат, направление тангенсов на вершину угла за направление оси Х, вычисляют координаты точек кривой по формулам

2) По φ и R определяют главные элементы кривой – Т (тангенс, касательная к кривой), Б (биссектриса), К (длина кривой), Д (домер).

3) Закрепляют главные точки кривой – нк, ск, кк.

Для этого от вершины угла при помощи рулетки по направлению к началу трассы откладывают Т. Полученная точка является нк и закрепляется деревянным колышком. Затем откладывают Т от ВУ по направлению на последующее направление трассы, получают, таким образом кк, которую тоже закрепляют колышком. Внутренний угол при помощи теодолита делят пополам и на полученном направлении откладывают Б, получают ск.φ – угол поворота трассы (в данном случае вправо); ВУ – вершина угла; нк – начало кривой; кк – конец кривой; ск – середина кривой. Эти точки называют главными точками кривой. R – радиус кривой.

---

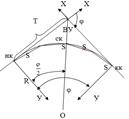
у₁=R-R·cosβ=R·(1-cosβ)=2R·sin²   х₁=R·sinβ; у₂=2R·sin²β; х₂=R·sin2β;

х_n=R·sinβ

у_n=2R·sin^{2   ;} β=   , ρ – радиан, единица плоского угла =206265″.

 Значения х_n, у_n можно выбирать из таблиц для разбивки круговых кривых.

4) Вдоль тангенсов от нк и кк откладывают при помощи рулетки значения х_n по перпендикуляру у_n и закрепляют полученные точки колышками.

Способ продолженных хорд

Заключается в следующем :

1.По значению S и R вычисляют х₁=Rsinβ; у₁=2Rsin²   и промежуточное перемещение в=   (из подобия равнобедренных треугольников ∆ (1-2' – 2) ∞ ∆ (1-2 – К) с равными вершинными углами β – в:S=S:R).

2.Точку 1 закрепляют колышком, отложив при помощи рулетки х₁ от начала кривой по направлению на вершину угла (по оси Х) и у₁ перпендикулярно этому направлению.



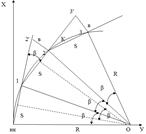
3.По точкам 0 – 1 натягивают ленту или рулетку и на продолжении 01 откладывают S, закрепляют точку 2'.

4.Точку 2 на кривой получают способом линейных засечек: пересечением отрезка S, который откладывают рулеткой из точки 1 и отрезка в, откладываемого из точки 2'. Полученную точку закрепляют деревянным колышком.

5.Таким же образом разбивают точки 3, 4, до середины кривой. Вторую половину кривой разбивают таким же образом от точки конца кривой.

Достоинство способа в том, что он применим на любой местности (косогоры, впадины и т.д.). Недостаток – с возрастанием длины кривой точность разбивки падает, так как положение последующей точки определяется относительно предыдущей. Происходит накопление ошибок.

Способ углов:

В этом способе используется то положение

---

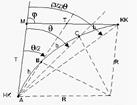
, что углы с вершиной в какой-либо точке круговой кривой образован касательной АМ(Т) и соответствующей секущей равны половине соответствующего центрального угла. Данный способ заключается в построении угла q/2 в начале системы координат и последовательном откладывании хорды. При заданной длине хорды угол y определяют по формуле:



где в – длина хорды.

Для разбивки промежуточных точек кривой, теодолит устанавливают в НК или КК, ориентируют его по линии тангенса и откладывают от этой линии угол q/2 . Отложив вдоль построенного направления хорду l, закрепляют первую точку (В). Затем, в той же точке НК строят угол 2q/2 и откладывают хорду (В-С), получая на пересечении направления угла и хорды точку 2, и т.д.

Линейные измерения выполняют вблизи кривой, что выгодно при разбивке точек на насыпи. Этот способ применяют для разбивки кривых земляных сооружений.

Порядок выполнения разбивки следующий:

- Выбирают из таблиц по радиусу угол Q/2 в зависимости от величины b (b=10,20,30 м).

- Устанавливают теодолит в точку А и от линии АМ фиксируют направление под углом Q/2.

- Вдоль этого направления откладывают длину хорды b и закрепляют на местности точку.

- Из точки А от направления АМ Фиксируют следующее направление под углом Q и вдоль него откладывают длину хорды. В такой последовательности выполняют разбивку всей кривой.

2. 
   В чем сущность геометрического нивелирования? Какие существуют способы геометрического нивелирования? Ответ дополнить схемой.
   

Нивелированием называется совокупность измерений на местности, в результате которых определяют превышения между точками местности с последующим вычислением их высот относительно принятой исходной поверхности. Такой исходной поверхностью обычно является основная уровенная поверхность, соответствующая среднему уровню воды морей и океанов в спокойном состоянии.

Знание высот точек земной поверхности необходимо при решении научных задач геодезии, связанных с изучением вертикальных движений земной коры, для высотного обоснования топографических съемок, изображения рельефа местности на планах и картах, решения различных инженерных задач при изысканиях, проектировании, строительстве и эксплуатации сооружений и т.п. Из известных методов нивелирования наиболее точным и распространенным в практике является геометрическое нивелирование.

---

Геометрическое нивелирование выполняют с помощью специальных геодезических приборов – нивелиров, обеспечивающих горизонтальное положение линии визирования в процессе измерений, и нивелирных реек. Превышения между точками определяют по отсчетам на рейках, отвесно устанавливаемых в этих точках. Различают два способа геометрического нивелирования.

При нивелировании вперед (рис.1 а) нивелир устанавливается в точке А, отметка которой Н_А известна, таким образом, чтобы окуляр зрительной трубы находился над этой точкой. В точке В отвесно устанавливают нивелирную рейку. С помощью рулетки или рейки измеряют высоту нивелира i, т.е. отвесное расстояние от центра окуляра до точки А, над которой установлен нивелир. Приводят визирную ось нивелира в горизонтальное положение и делают отсчет b по рейке. Как следует из рисунка 14.1 а:

h = i – b.

Величина ГП = Н_А + i представляет собой высоту визирного луча нивелира над уровенной поверхностью и называется горизонтом прибора.

При нивелировании из середины (рис.1 б) нивелир устанавливается на одинаковых расстояниях между точками А и В, в которых отвесно устанавливают рейки. Приводят визирную ось нивелира в горизонтальное положение и, последовательно визируя на рейки, берут отсчеты: по задней рейке – а, по передней рейке – b. Тогда превышение точки В над точкой А составит:

h = a – b.

Превышение будет положительным, если передняя точка выше задней, и отрицательным, если передняя точка ниже задней.

Способ нивелирования из середины имеет заметные преимущества по сравнению с нивелированием вперед, т.к. в два раза повышает производительность труда и позволяет исключить влияние ряда погрешностей на точность определения превышений.



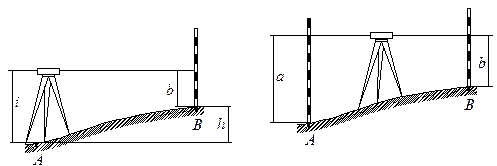
а б

где а – нивелирование вперед;

б – нивелирование из середины.

Рисунок 1. – Схемы геометрического нивелирования.

 Геометрическое нивелирование независимо от способа его выполнения может быть простым и последовательным. Если превышение между двумя точками местности получают в результате одной установки нивелира, то такое нивелирование называется простым. Если нивелирование выполняют с целью передачи отметок на значительное расстояние либо с целью построения профиля местности, то оно производится с нескольких станций и называется последовательным или сложным.

---

3. 
   Чем руководствуются при проведении проектной линии? Как вычисляются проектные и рабочие отметки?
   

Проектные отметки вычисляют по уклону проектной линии, а уклон — по высотам отдельных фиксированных точек. С использованием отметок таких точек уклон проектной линии вычисляют по формуле:



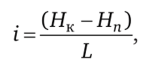
где i — уклон проектной линии; Нк — проектная отметка конца линии; Нп — проектная отметка начала линии; L — длина горизонтального проложения линии.
Отметки всех других точек данной проектной линии получают по формуле:



где Н_п+1 — проектная отметка предыдущей точки; Н_п — проектная отметка последующей точки; i — расстояние между этими точками.

Рабочая отметка

Рабочая отметка — это разность между проектной отметкой и отметкой земли, т. е.



где Н_кр — проектная отметка (красная); Н_чер — отметка земли (черная); h_раб — рабочая отметка.

Рабочая отметка показывает, на какую величину необходимо срезать или насыпать грунт в данной точке.

Точка нулевых работ

Точка нулевых работ — точка пересечения проектной линии с профилем земли. Она расположена в месте перехода насыпи в выемку или, наоборот, выемки в насыпь, т. е. между рабочими отметками, имеющими противоположные знаки.

Расстояние точки нулевых работ от заднего пикета вычисляется по формуле:



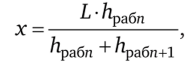
где х — расстояние точки нулевых работ от заднего пикета; L — длина линии пикета; hpa6n — рабочая отметка предыдущего пикета; hpa6n+l — рабочая отметка последующего пикета.

---

Смотрите также файлы

• Тема 8 Творческое задание.docx

• Электронды кестелер кмегімен есептерді шешу Педагогты атыжні.docx

• Педагогический совет Инновационные технологии в дошкольном образовательном учреждении Цели.docx

• Использованием икт в профессиональной деятельности учителя информатики.docx

• Задание Измерение превышений способом из середины Журнал нивелирования.docx