Файл: Контрольная работа по дисциплине Электротехника и электроника Студент группы лэ90682 И. Е. Чилигин.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.05.2024
Просмотров: 23
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство транспорта Российской Федерации
Омский государственный университет путей сообщения (ОмГУПС)
Кафедра «Электрических машин и общей электротехники»
Контрольная работа
по дисциплине: «Электротехника и электроника»
Студент группы:
ЛЭ-90682
______ И.Е. Чилигин
Руководитель:
К.т.н.,доц. каф Теоретичская
электротехника
______А.В. Пономарев
Омск 2021
Контрольная работа №1
Расчет цепи постоянного тока с одним источником энергии
Определить эквивалентное сопротивление цепи относительно зажимов источника ЭДC; определить токи ветвей и напряжение Uab, используя закон Ома.
| Дано: E = 60 В R1 = 6 Ом R2 = 9 Ом R3 = 6 Ом R4 = 10 Ом | Решение. 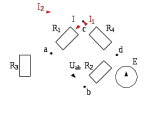 Рисунок 1 – Расчетная схема |
| Rэкв – ? Ii – ? Uab – ? |
Определение эквивалентного (входного) сопротивления Rэкв
Преобразуем участок с последовательным соединением элементов R2 и R3, заменив их суммарным сопротивлением R23, которое определяется по выражению:
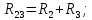
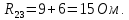
Преобразуем участок с параллельным соединением элементов R4 и R23, заменив их суммарным сопротивлением R234, которое определяется по выражению:
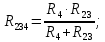
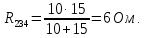
Входное (эквивалентное) сопротивление цепи Rэкв относительно источника ЭДС Е определим, осуществив последнее преобразование: заменим два последовательно соединенных сопротивления R1 и R234 одним эквивалентным:
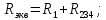
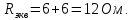
Определение токов ветвей
Входной ток определяется по закону Ома
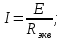
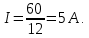
Для определения остальных токов ветвей необходимы значения напряжений, приложенных к ветвям, и сопротивлений этих ветвей.
Токи I1 и I2 протекают по ветвям, расположенным между узлами c и d. Напряжение, приложенное к указанным ветвям, рассчитывается по выражению:
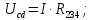
тогда
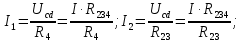
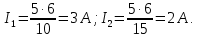
Определение напряжения Uab.
Напряжение Uab определим через потенциалы точек. Примем потенциал точки a равным нулю. Пройдем от точки a к точке b через сопротивления R1, R4 и R2. Ток в сопротивлении протекает от большего потенциала к меньшему, поэтому потенциал точки с будет больше потенциала точки a и определится по выражению:
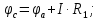
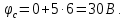
Далее определим потенциал точки d, который по аналогии с предыдущими рассуждениями, будет больше потенциала точки c на величину падения напряжения на сопротивлении R4 от тока I1 и определится следующим образом:
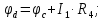
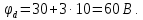
Потенциал точки b, по аналогии с предыдущими рассуждениями, будет меньше потенциала точки d на величину падения напряжения на сопротивлении R2 от тока I2 и определится следующим образом:
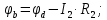
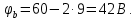
Напряжение Uab является разностью потенциалов точек a и b:
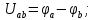
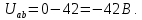
Ответ:
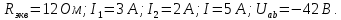
Контрольная работа №2
Расчет цепи постоянного тока с несколькими источниками энергии
Определить токи I1-I6 методом узловых потенциалов; составить уравнения для определения токов I1-I6 методом контурных токов, найти значения токов и сравнить результаты с полученными по методу узловых потенциалов; проверить баланс мощностей; составить уравнения по законам Кирхгофа для определения токов I1-I6, подставить в уравнения значения токов, найденные по методу узловых потенциалов, убедиться в том, что получаются тождества.
| Дано: R1 = 10 Ом R2 = 10 Ом R3 = 5 Ом R4 = 10 Ом R5 = 10 Ом E1 = 10 В E2 = 10 В E3 = 20 В J = 5 A | Решение. 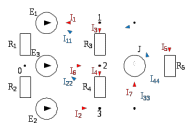 Рисунок 1 – Расчетная схема |
| |
Определение токов методом узловых потенциалов.
Ветвь между узлами 0 и 2 содержит идеальный источник ЭДС E3 с нулевым внутренним сопротивлением. В этом случае за базисный узел (узел с нулевым потенциалом) принимается тот, который принадлежит ветви с идеальным источником ЭДС (узел 0 или 2). Пусть φ0 = 0 В. Тогда потенциал узла 2 определяется следующим выражением:
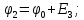
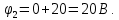
Неизвестными являются потенциалы двух узлов – φ1 и φ3. Достаточно составить систему из двух уравнений, где должны быть учтены связи с потенциалом φ2:
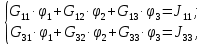
где G11 и G33 – собственная проводимость первого и третьего узлов соответственно;
G13 = G31, G12 и G32 – взаимная проводимость между узлами, номера которых указаны в индексах;
J11, J33 – задающий ток первого и третьего узлов соответственно.
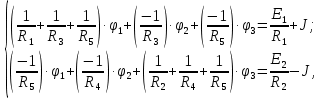
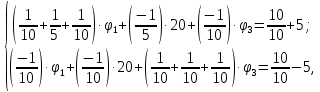
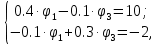
Умножим первое уравнение на 3 и сложим со вторым
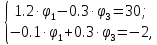
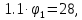
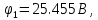
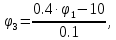
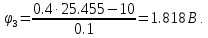
C учетом известных потенциалов φ0 = 0 и φ2 = E3 рассчитываем токи ветвей по закону Ома:
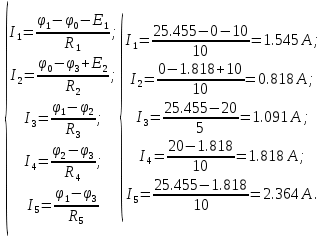
Ток I6 в ветви с идеальным источником ЭДС находим по первому закону Кирхгофа:
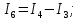
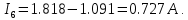
Ток I7 в ветви с источником тока известен и равен току источника тока:
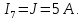
Определение токов ветвей методом контурных токов.
Схема содержит четыре независимых контура. Выберем произвольное направление контурных токов. В общем виде система уравнений относительно трех неизвестных контурных токов имеет вид (для контура с источником тока уравнение не составляется, так как I44 = J):
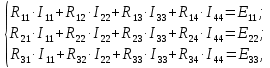
где R11, R22 и R33 – собственные сопротивления соответствующих контуров;
R13 = R31, R12 = R21, R23 = R32 – взаимное сопротивление между контурами;
E11, E22 и E33 – контурные ЭДС.
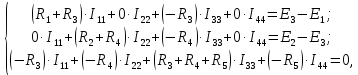
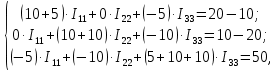
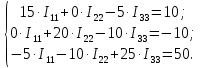
По правилу Крамера определяем контурные токи:
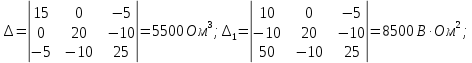
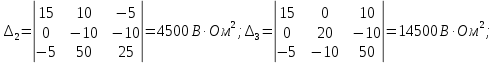
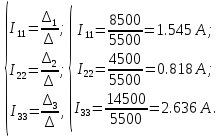
В итоге токи ветвей определяются следующим образом:
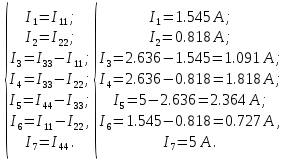
Как видно из расчета значения токов совпадают со значениями, полученными в результате расчета по методу узловых потенциалов (таблица 1).
Таблица 1 – Значения токов, полученные различными методами
| Метод получения результата | Ток, А | ||||||
| I1 | I2 | I3 | I4 | I5 | I6 | I7 | |
| Метод контурных токов | 1.545 | 0.818 | 1.091 | 1.818 | 2.364 | 0.727 | 5 |
| Метод узловых потенциалов | 1.545 | 0.818 | 1.091 | 1.818 | 2.364 | 0.727 | 5 |
Проверка баланса мощностей.
Мощность источников определяется выражением:
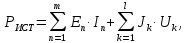
где m – количество источников ЭДС;
l– количество источников тока;
In – ток, протекающий по источнику ЭДС En;
Uk – напряжение, приложенное к источнику тока Jk.
Для заданной цепи мощность источников определяется по формуле:
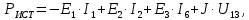
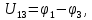
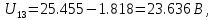
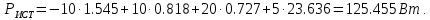
Мощность потребителей рассчитывается так
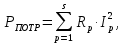
где s – количество сопротивлений в цепи,
Ip – ток, протекающий по сопротивлению Rp.
Для заданной цепи мощность потребителей рассчитывается по выражению:
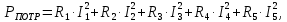
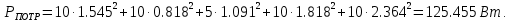
Расхождение между значениями мощности источников и потребителей определяется как
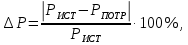
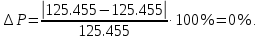
Составление уравнений по законам Кирхгофа
