Файл: Контрольная работа по дисциплине Электротехника и электроника Студент группы лэ90682 И. Е. Чилигин.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.05.2024
Просмотров: 25
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
В схеме шесть неизвестных значений тока, следовательно, необходимо составить шесть уравнений по законам Кирхгофа.
В схеме на рисунке 1 четыре узла, поэтому по первому закону Кирхгофа составляем три уравнения (на одно меньше, чем количество узлов); остальные три уравнения составляем по второму закону Кирхгофа, выбирая независимые контуры.
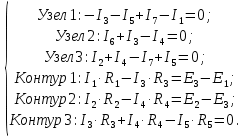
Подставив в уравнения рассчитанные значения тока, убедимся в том, что получились тождества:
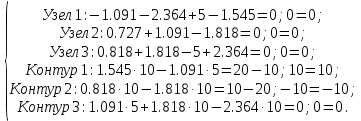
Контрольная работа №3
Расчет цепи синусоидального тока
Определить комплексное входное сопротивление; рассчитать действующие значения тока во всех ветвях схемы, записать выражения для его мгновенных значений; проверить баланс мощностей; рассчитать действующие значения напряжения на всех элементах схемы, построить топографическую диаграмму.
Приложенное мгновенное напряжение
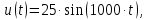
где угловая частота
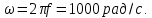
Тогда действующее значение напряжения в комплексной форме
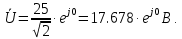
Определение комплексного входного сопротивления цепи.
Эквивалентная схема замещения для расчета комплексных сопротивлений ветвей приведена на рисунке 2.
Рисунок 2 – Эквивалентная схема замещения
Комплексные сопротивления ветвей цепи рассчитываются по формулам, Ом:
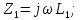
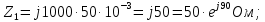
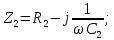
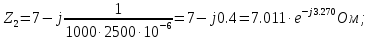
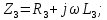
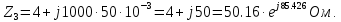
Комплексное сопротивление участка параллельного соединения ветвей cd рассчитывается по формуле:
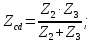
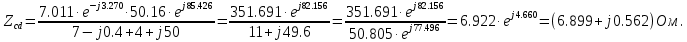
Комплексное входное сопротивление заданной цепи определим по формуле:
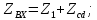
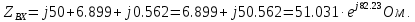
Расчет токов ветвей.
По закону Ома входной ток
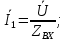
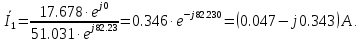
Мгновенное значение входного тока определяется функцией
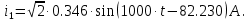
Для определения токов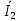
, 
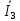необходимо знать напряжение 
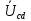, приложенное к ветвям, по которым протекают токи. По закону Ома напряжение 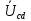рассчитывается по выражению:
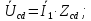
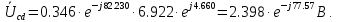
Разделим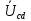 на сопротивления соответствующих ветвей и найдем токи:
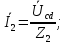
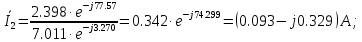
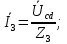
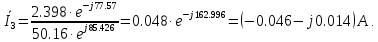
Мгновенные значения токов i2 и i3:
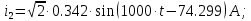
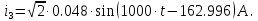
По первому закону Кирхгофа для узла с:
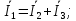
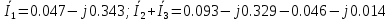
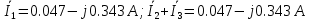
Таким образом, первый закон Кирхгофа выполняется. Следующей проверкой правильности расчета тока ветвей является составление баланса мощностей.
Проверка баланса мощностей.
Полная комплексная мощность
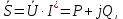
где P и Q – активная и реактивная мощности, представляющие собой, соответственно, действительную и мнимую части произведение действующего комплексного значения напряжения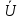
на сопряженной действующее комплексное значение тока 
:
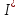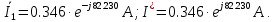
Комплексная мощность источников ЭДС в общем случае рассчитывается по формуле
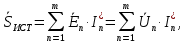
где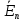
и 
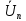– комплексные действующие значения ЭДС и напряжения источника;
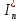– комплексное действующее сопряженное значение тока, протекающего по n-му источнику;
m – количество источников ЭДС.
Полная комплексная мощность данной цепи:
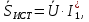
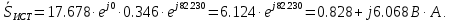
Активная и реактивная мощности источников есть соответствующие действительные и мнимые части полной, т.е.
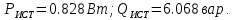
Активная и реактивная мощности приемников (сопротивлений) определяется по следующим формулам:
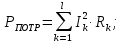
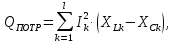
где Rk – активное сопротивление k-й ветви,
XLk и XCk – индуктивное и емкостное сопротивления k-й ветви,
Ik – действующее значение тока k-й ветви,
l – количество ветвей.
Для заданной цепи активная и реактивная мощности определяются как:
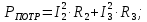
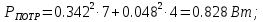
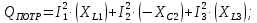
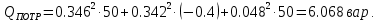
Расхождение между значениями мощностей источников и приемников:
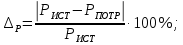
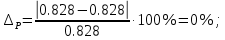
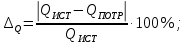
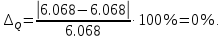
Построение топографической диаграммы.
При построении топографической диаграммы напряжений учитывают фазовый сдвиг между вектором тока, протекающего через элемент электрической цепи (сопротивление, индуктивность, емкость), и вектором падения напряжения на нем. На активном сопротивлении эти векторы совпадают по направлению, на индуктивности вектор напряжения опережает вектор тока на угол 900, на емкости – отстает на 900.
Построение топографической диаграммы начнем с точки а (примем потенциал данной точки за ноль) в направлении обхода по часовой стрелке.
Рассчитаем значения падения напряжения на всех элементах схемы
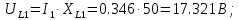
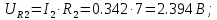
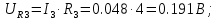
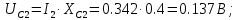
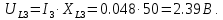
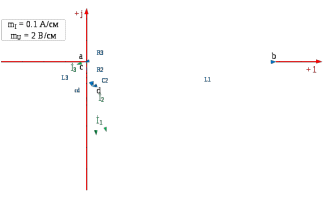
Рисунок 3 – Векторная диаграмма
Контрольная работа №4
Исследование резонансов в цепях синусоидального тока
Определить, какой резонанс (напряжения или тока) возможен в заданной цепи, и рассчитать указанный в условии задачи резонансный параметр.
Индуктивность и емкость в заданной цепи соединены последовательно, поэтому в цепи возможен резонанс напряжений. Условием резонанса напряжений является равенство нулю мнимой части входного комплексного сопротивления цепи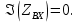
Входное сопротивление данной цепи определяется выражением:
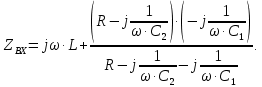
Преобразуем полученное выражение, умножив числитель и знаменатель второго слагаемого на комплексное,
сопряженное знаменателю выражение, и выделим действительную и мнимую части:
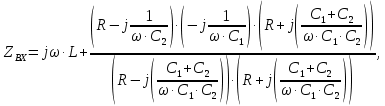
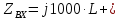
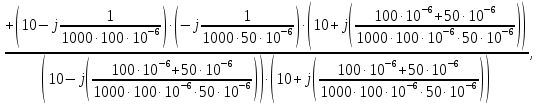
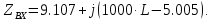
По условию резонанса напряжений мнимая часть комплексного входного сопротивления равна нулю:
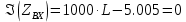
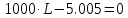
Откуда
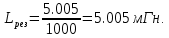
Ответ: Lрез = 5.005 мГн.
5 Расчёт несимметричной трёхфазной цепи
Задача расчета токов и напряжений в трехфазной электрической цепи усложняется, если хотя бы в одном ее месте нарушено условие симметрии: несимметрична трехфазная система ЭДС или источников тока, различны параметры соответствующих элементов фаз. В таких случаях всю трехфазную цепь рассматривают как разветвленную цепь с несколькими однофазными источниками.
Рисунок 5.1 – Схема трехфазной электрической цепи
Параметры элементов цепи:
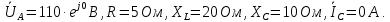
Найти токи в ветвях, составить баланс мощностей, построить векторную диаграмму токов и напряжений.
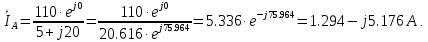
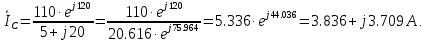
По первому закону Кирхгофа:
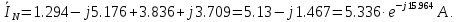
Составим баланс мощностей.
Комплексная мощность источника:
В схеме шесть неизвестных значений тока, следовательно, необходимо составить шесть уравнений по законам Кирхгофа.
В схеме на рисунке 1 четыре узла, поэтому по первому закону Кирхгофа составляем три уравнения (на одно меньше, чем количество узлов); остальные три уравнения составляем по второму закону Кирхгофа, выбирая независимые контуры.
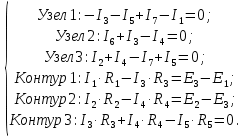
Подставив в уравнения рассчитанные значения тока, убедимся в том, что получились тождества:
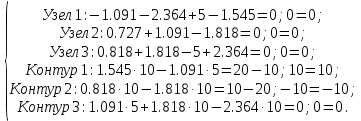
Контрольная работа №3
Расчет цепи синусоидального тока
Определить комплексное входное сопротивление; рассчитать действующие значения тока во всех ветвях схемы, записать выражения для его мгновенных значений; проверить баланс мощностей; рассчитать действующие значения напряжения на всех элементах схемы, построить топографическую диаграмму.
| Дано: R2 = 7 Ом R3 = 4 Ом L1 = 50 мГн L3 = 50 мГн C2 = 2500 мкФ u(t) = 25∙sin(1000∙t) В | Решение.  Рисунок 1 – Расчетная схема |
| |
Приложенное мгновенное напряжение
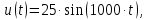
где угловая частота
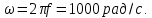
Тогда действующее значение напряжения в комплексной форме
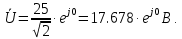
Определение комплексного входного сопротивления цепи.
Эквивалентная схема замещения для расчета комплексных сопротивлений ветвей приведена на рисунке 2.
Рисунок 2 – Эквивалентная схема замещения
Комплексные сопротивления ветвей цепи рассчитываются по формулам, Ом:
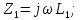
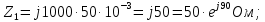
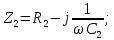
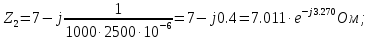
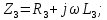
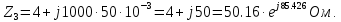
Комплексное сопротивление участка параллельного соединения ветвей cd рассчитывается по формуле:
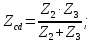
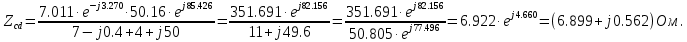
Комплексное входное сопротивление заданной цепи определим по формуле:
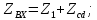
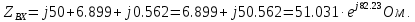
Расчет токов ветвей.
По закону Ома входной ток
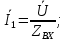
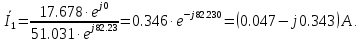
Мгновенное значение входного тока определяется функцией
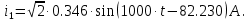
Для определения токов
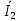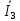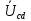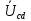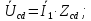
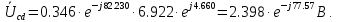
, необходимо знать напряжение , приложенное к ветвям, по которым протекают токи. По закону Ома напряжение рассчитывается по выражению: Разделим
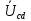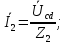
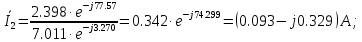
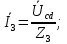
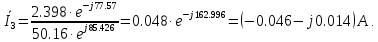
на сопротивления соответствующих ветвей и найдем токи: Мгновенные значения токов i2 и i3:
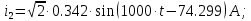
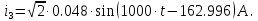
По первому закону Кирхгофа для узла с:
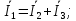
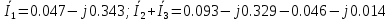
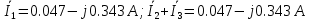
Таким образом, первый закон Кирхгофа выполняется. Следующей проверкой правильности расчета тока ветвей является составление баланса мощностей.
Проверка баланса мощностей.
Полная комплексная мощность
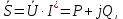
где P и Q – активная и реактивная мощности, представляющие собой, соответственно, действительную и мнимую части произведение действующего комплексного значения напряжения
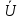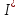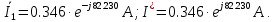
на сопряженной действующее комплексное значение тока : Комплексная мощность источников ЭДС в общем случае рассчитывается по формуле
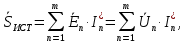
где
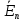и 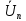– комплексные действующие значения ЭДС и напряжения источника; 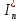– комплексное действующее сопряженное значение тока, протекающего по n-му источнику;m – количество источников ЭДС.
Полная комплексная мощность данной цепи:
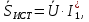
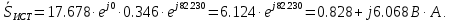
Активная и реактивная мощности источников есть соответствующие действительные и мнимые части полной, т.е.
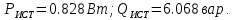
Активная и реактивная мощности приемников (сопротивлений) определяется по следующим формулам:
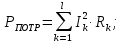
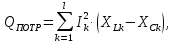
где Rk – активное сопротивление k-й ветви,
XLk и XCk – индуктивное и емкостное сопротивления k-й ветви,
Ik – действующее значение тока k-й ветви,
l – количество ветвей.
Для заданной цепи активная и реактивная мощности определяются как:
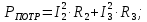
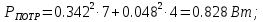
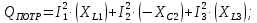
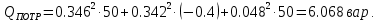
Расхождение между значениями мощностей источников и приемников:
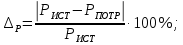
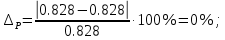
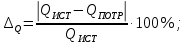
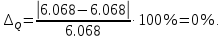
Построение топографической диаграммы.
При построении топографической диаграммы напряжений учитывают фазовый сдвиг между вектором тока, протекающего через элемент электрической цепи (сопротивление, индуктивность, емкость), и вектором падения напряжения на нем. На активном сопротивлении эти векторы совпадают по направлению, на индуктивности вектор напряжения опережает вектор тока на угол 900, на емкости – отстает на 900.
Построение топографической диаграммы начнем с точки а (примем потенциал данной точки за ноль) в направлении обхода по часовой стрелке.
Рассчитаем значения падения напряжения на всех элементах схемы
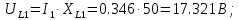
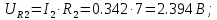
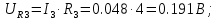
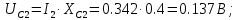
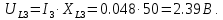
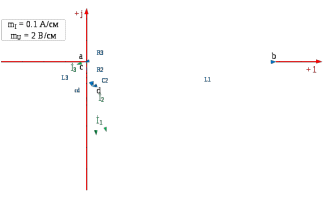
Рисунок 3 – Векторная диаграмма
Контрольная работа №4
Исследование резонансов в цепях синусоидального тока
Определить, какой резонанс (напряжения или тока) возможен в заданной цепи, и рассчитать указанный в условии задачи резонансный параметр.
| Дано: ω = 1000 рад/с C1 = 0.1·10-4 Ф C2 = 2.32·10-4 Ф R = 10 Ом | Решение.  Рисунок 1 – Расчетная схема |
| Lрез – ? |
Индуктивность и емкость в заданной цепи соединены последовательно, поэтому в цепи возможен резонанс напряжений. Условием резонанса напряжений является равенство нулю мнимой части входного комплексного сопротивления цепи
Входное сопротивление данной цепи определяется выражением:
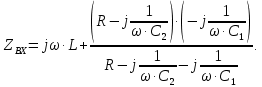
Преобразуем полученное выражение, умножив числитель и знаменатель второго слагаемого на комплексное,
сопряженное знаменателю выражение, и выделим действительную и мнимую части:
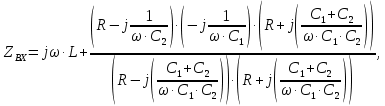
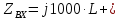
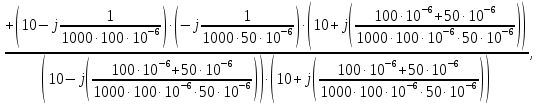
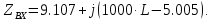
По условию резонанса напряжений мнимая часть комплексного входного сопротивления равна нулю:
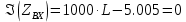
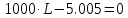
Откуда
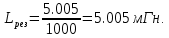
Ответ: Lрез = 5.005 мГн.
5 Расчёт несимметричной трёхфазной цепи
Задача расчета токов и напряжений в трехфазной электрической цепи усложняется, если хотя бы в одном ее месте нарушено условие симметрии: несимметрична трехфазная система ЭДС или источников тока, различны параметры соответствующих элементов фаз. В таких случаях всю трехфазную цепь рассматривают как разветвленную цепь с несколькими однофазными источниками.
Рисунок 5.1 – Схема трехфазной электрической цепи
Параметры элементов цепи:
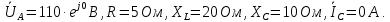
Найти токи в ветвях, составить баланс мощностей, построить векторную диаграмму токов и напряжений.
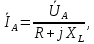 | (5.1) |
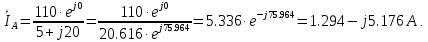
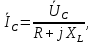 | (5.2) |
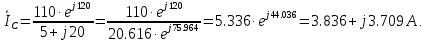
По первому закону Кирхгофа:
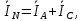 | (5.3) |
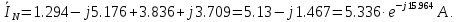
Составим баланс мощностей.
Комплексная мощность источника: