Файл: Лабораторная работа 5 трехфазные цепи. Соединение звездой цель и задачи работы.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.05.2024
Просмотров: 8
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ЛАБОРАТОРНАЯ РАБОТА №5
ТРЕХФАЗНЫЕ ЦЕПИ. СОЕДИНЕНИЕ ЗВЕЗДОЙ
Цель и задачи работы:
Целью работы является ознакомление с особенностями режимов
работы трех- и четырехпроводных трехфазных цепей при соединении
источника и потребителя в звезду.
Задача 1. Измерить фазные напряжения, линейные напряжения, токи
в различных режимах работы трехфазной цепи.
Задача 2. Построить векторные диаграммы напряжений и токов для
каждого режима.
Последовательность выполнения работы
1. Измерить сопротивления всех резисторов, а также определить
емкость конденсатора и индуктивность катушки, которые будут входить в
электрическую цепь.
2. Собрать электрическую цепь согласно рис. 1. Нулевой провод
исключить из цепи.
3. Измерить фазные и линейные напряжения, а также напряжение
между нулевыми точками для трехпроводной цепи при всех режимах,
указанных в таблице 5.1. Результаты занести в эту таблицу. Единицы
измерения: напряжение в вольтах, сопротивления в Омах, ток в амперах.
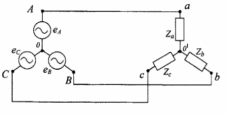 |
| Рисунок 1 – Схема соединения «Звезда без нейтрали» |
Таблица 5.1
| Режим | Эксперимент | Расчет | |||||||||||
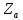 , Ом , Ом | 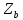 , Ом , Ом | 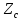 , Ом , Ом | 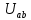 , В , В | 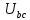 , В , В | 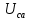 , В , В | 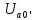 , В , В | 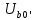 , В , В |  , В , В | 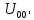 , В , В | 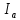 , А , А | 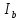 , А , А | 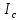 , А , А | |
| 1. Симметричный режим | 53,2 | 52,5 | 52,9 | 23 | 22,7 | 23,3 | 13,3 | 12,8 | 13,2 | 0,3 | 0,25 | 0,25 | 0,25 |
| 2. Неравномерная нагрузка | 24 | 52,5 | 52,9 | 22,8 | 23 | 23 | 9,6 | 15 | 15,1 | 2,9 | 0,4 | 0,28 | 0,28 |
| 3. Короткое замыкание | 0 | 52,5 | 52,9 | 22,8 | 23 | 22,9 | 0,4 | 22,7 | 22,8 | 12,5 | 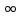 | 0,43 | 0,43 |
| 4. Обрыв фазы нагрузки | 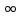 | 52,5 | 52,9 | 23,3 | 22,9 | 23,5 | 20 | 11,4 | 11,1 | 6,4 | 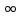 | 0,21 | 0,21 |
Расчеты.
Определим линейные напряжения для данной схемы типа «звезда»:
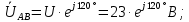
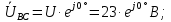
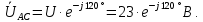
Определим фазные напряжения для данной схемы типа «звезда»:
Зная, что линейные и фазные напряжения связаны следующим соотношением:
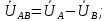
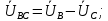
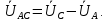
Выражаем фазные напряжения:
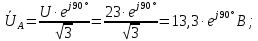
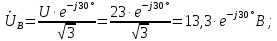
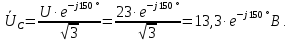
Определим комплексные эквивалентные сопротивления каждой фазы:
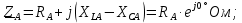
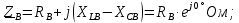
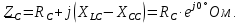
Определим фазные токи (для соединения типа «звезда» фазные токи равны линейным):
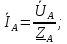
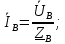
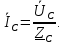
-
Если нагрузка симметричная:
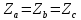
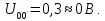
В этом случае линейные токи
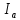 ,
, 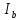 ,
,  образуют симметричную систему векторов:
образуют симметричную систему векторов: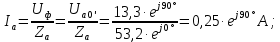
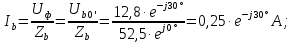
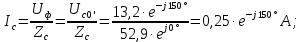
Естественно, что:
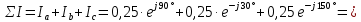
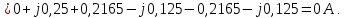
-
Если нагрузка неравномерная, то токи в фазах будут найдены:
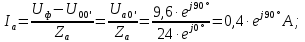
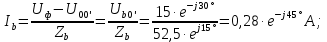
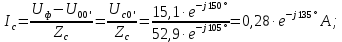
Линейные токи по отношению друг к другу могут находиться под любым углом, т.е. образуют несимметричную систему векторов. По первому закону Кирхгофа их сумма равняется нулю:

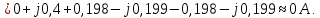
-
Если происходит короткое замыкание на нагрузке фазы А, то ее сопротивление становится минимальным. В результате этого ток в фазе возрастает до высоких значений. А фазные напряжения в оставшихся фазах возрастут до линейных значений.
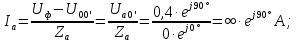
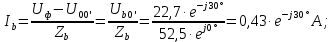
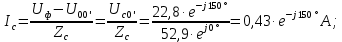
Линейные токи по отношению друг к другу находятся противоположно друг другу, результирующее значение равно нулю. По первому закону Кирхгофа их сумма равняется нулю:
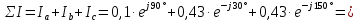
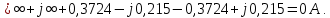
-
Если происходит обрыв нагрузки фазы А, то ее сопротивление становится огромным, потому что образован разрыв. В результате этого ток в фазе А будет равен нулю. Напряжения на разорванной фазе возрастет. А фазные напряжения на оставшихся фазах разделятся в поровну от линейного.
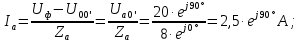
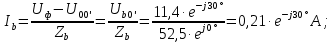
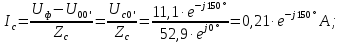
Линейные токи по отношению друг к другу находятся противоположно друг другу, результирующее значение равно нулю. По первому закону Кирхгофа их сумма равняется нулю:
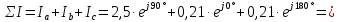
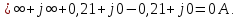
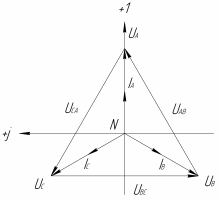 |
| Рисунок 1 – Симметричный режим |
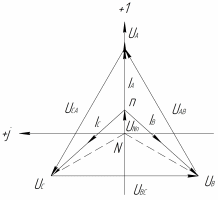 |
| Рисунок 2 – Неравномерная нагрузка |
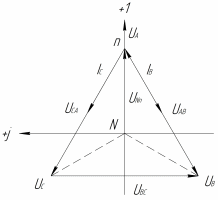 |
| Рисунок 3 – Короткое замыкание |
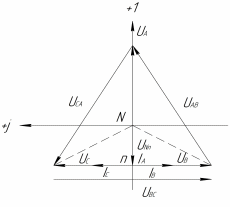 |
| Рисунок 4 – Обрыв фазы нагрузки |
СПИСОК ЛИТЕРАТУРЫ
1. Демирчян К.С. Теоретические основы электротехники: в 3 т. / К. С. Демирчян, Л. Р. Нейман, Н. В. Коровкин, В. Л. Чечурин. – СПб. : Питер,
2006. Т.1 – 463 с.
2. Зыкин Ф.А. Методические указания к лабораторным работам по
теоретическим основам электротехники / Ф. А. Зыкин, Т. С. Чистякова. –
Ульяновск : УлГТУ, 1997. – 60 с.
