Теория вероятностей и математическая статистика

Задание на расчетную работу №1

«Основы статистики»

1. Группировка по отдельным значениям признака

Пусть 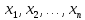— выборка объема 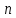из некоторой генеральной совокупности. По этой выборке можно оценить основные числовые характеристики генеральной совокупности. Различные элементы выборки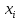

называются вариантами. Ряд вариант, расположенных в порядке возрастания их значений называется вариационным рядом. Им пользуются, в основном, при малых 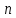. Если 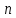велико, то ряд преобразуют в группировки по отдельным значениям признака 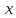(дискретная группировка) или по интервалам изменения признака (интервальная группировка), для чего разбивают диапазон изменения признака 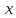, называемый размахом 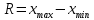на 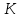равных интервалов. Для определения количества интервалов рекомендуется правило 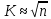, где 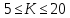. Можно пользоваться и другими эмпирическими формулами, например, формулой Стерджеса 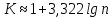, но они дают приблизительно одинаковый результат.

Последовательность 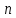значений 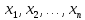, полученных в результате наблюдения некоторого процесса, мы будем рассматривать как совокупность значений одинаково распределенных независимых случайных величин

---

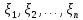, Представляющих собой экземпляров одной и той же случайной величины 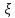. Эта последовательность значений называется выборкой. В этом случае говорят, что выборка взята из генеральной совокупности случайной величины 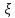. Если величина 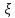следует закону распределения 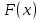, то мы будем говорить. что генеральная совокупность распределена по закону .

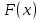Варианты, попадающие на границу интервала, отнесены к левому интервалу (можно отнести их и к правому интервалу, а в том случае, если на границу попадает много вариант, можно их поделить пополам между соседними интервалами).

Результат группировки представляют рядом вариант или интервалов вариант, расположенных в порядке их возрастания и рядом соответствующих частот. Под частотой 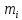признака или интервала понимают число членов выборки с заданной вариантой 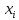или число членов выборки, варианты которых лежат в -м интервале. Относительной частотой 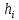называется отношение частоты 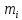к объему всей выборки 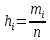. Таким образом, если проведена группировка, то значению 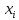или -му интервалу 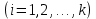будут отвечать частоты 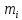и относительные частоты 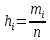, при этом 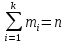и 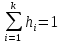, а все выборочные значения, попавшие в 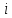-й интервал, заменяются серединой интервала

---

.

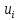2. Вычисление числовых характеристик выборки

Пусть – выборка объема из генеральной совокупности, имеющей функцию распределения . Числовые характеристики выборки называются выборочными (эмпирическими) числовыми характеристиками. Основные числовые характеристики:

• 
  среднее арифметическое (выборочное среднее):
  

• 
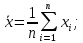
  выборочная дисперсия:
  

• 
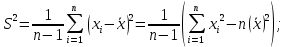
  стандартное (среднее квадратическое) отклонение является корнем из выборочной дисперсии:
  

• 
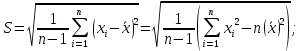
  коэффициент вариации:
  

• 
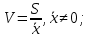
  выборочные начальные и центральные моменты порядка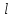 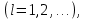определяются по формулам:
  

• 
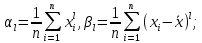
  оценка коэффициента асимметрии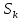 характеризует симметричность распределения относительно среднего 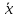, и определяется по формуле:
  

• 
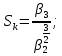
  оценка эксцесса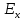 – меры островершинности распределения по сравнению с нормальным распределением:
  

• 
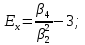
  выборочная мода :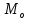
  

Для дискретного вариационного ряда (дискретная группировка) мода определяется как значение варианты с наибольшей частотой, если выборка достаточно большая.

При интервальной группировке выбирается интервал, которому соответствует наибольшая частота. Пусть это k-й интервал

---

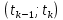, его частота равна 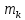, а ширина 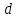, тогда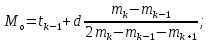

• 
  выборочная медиана :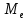
  

Определяется, как значение признака, относительно которого выборка делится на две равные по объему части. Если выборка объема представлена вариационным рядом, то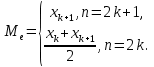



При интервальной группировке (интервальный вариационный ряд) сначала находят так называемый медианный интервал 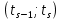, номер 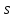которого определяют из неравенств: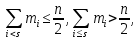



где 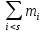– сумма частот всех интервалов левее медианного, 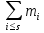– сумма частот, включающая частоту медианного интервала.

Медиану оценивают с помощью следующей интерполяционной формулы:

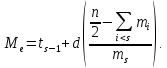
3. Предварительная проверка на нормальность

С помощью вычисленных числовых характеристик можно определить, является ли выборочное распределение близким к нормальному закону. Если выборочное распределение близко к нормальному закону (или является таковым), то:

1) в интервалы 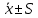, 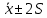и 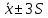должны попадать соответственно приблизительно 68%, 95% и 100% выборочных значений;

2) Оценка эксцесса и коэффициента асимметрии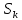

---

‚ должны быть близки к нулю;

3) .

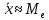4. Графическое представление выборочного распределения

Наиболее распространенными способами графического представления эмпирических данных (выборки) являются гистограмма, полигон частот и эмпирическая функция распределения (накопленные относительные частоты).

Пусть 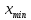и 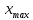— соответственно наименьшее и наибольшее значения варнант выборки. Величина называется размахом выборки. Размах делится на число интервалов (интервальная группировка), которое можно вычислить по одной из следующих формул: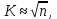







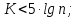
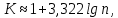
округлив до целого числа.

Обычно предполагают, что количество интервалов должно удовлетворять условию .

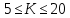Ширина каждого интервала вычисляется по формуле 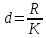. После разбиения на интервалы определяют:

• 
  абсолютные частоты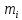 , , 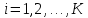где 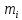- количество элементов выборки, попавших в 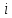— й интервал (элемент, попавший на границу интервала, относят к какому-нибудь выбранному интервалу, например, левому, или правому; если на границу интервала попадает много элементов выборки, то их делят пополам между левым и правым интервалами);
  
• 
  относительные частоты ;
  
• 
  относительные накопленные частоты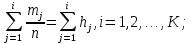
  
• 
  середины интервалов .
  

---

Смотрите также файлы

• Заказчик обязан заплатить, если пользуется результатом работ по назначению. Обзор практики по спорам из договоров подряда в 2022 году.doc

• Сущность административного права.docx

• Профессиональная ориентация школьников.docx

• Аналитическая деятельность педагога содержание, результаты, пути совершенствования.docx

• Формулы вежливости.docx