Файл: Теория вероятностей и математическая статистика Задание на расчетную работу 1 Основы статистики.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.05.2024
Просмотров: 23
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Все полученные результаты сводятся в таблицу.
| Номер интервала | Границы интервалов | 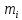 |  | 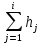 |  |
| 1 | | 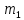 | 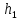 | 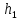 | 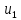 |
| 2 | | 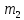 | 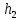 | 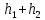 | 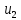 |
| … | | … | … | … | … |
При этом
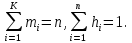
Гистограмма строится следующим образом. На оси абсцисс откладываются интервалы, и на каждом из них строится прямоугольник, площадь которого равна относительной частоте, соответствующей этому интервалу, т.е. высота прямоугольника (ордината) равна
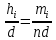 , так что полная площадь гистограммы равна 1. Таким образом, гистограмма является эмпирическим аналогом плотности распределения. Так как множители
, так что полная площадь гистограммы равна 1. Таким образом, гистограмма является эмпирическим аналогом плотности распределения. Так как множители 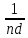 можно рассматривать как масштабные, то по оси ординат можно откладывать частоты
можно рассматривать как масштабные, то по оси ординат можно откладывать частоты 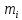 или
или  , (правда, в этом случае площадь всех прямоугольников будет равна
, (правда, в этом случае площадь всех прямоугольников будет равна 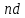 ).
).Полигон частот - ломаная линия, которая получается, если из середины
каждого интервала
 восстановить перпендикуляр высотой
восстановить перпендикуляр высотой  (или
(или 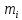 ) и соединить вершины этих перпендикуляров. Полигон частот чаще используют
) и соединить вершины этих перпендикуляров. Полигон частот чаще используютпри дискретной группировке.
-
Задание
-
Выполнить группировку исходных данных своего варианта по значению признака. -
Вычислить основные числовые характеристики:-
Выборочное среднее. -
Выборочную дисперсию. -
Стандартное отклонение. -
Коэффициент вариации. -
Оценка коэффициента асимметрии. -
Оценка эксцесса. -
Выборочная мода. -
Выборочная медиана.
-
-
Выполнить предварительную проверку на нормальность. -
Построить гистограмму и полигон частот.
-
Пример выполнения
Для выполнения задания будем использовать выборку объемом 15 элементов:
Выполним группировку исходных данных по значению признака. Для этого упорядочим выборку по возрастанию, и, используя формулы =МИН() и =МАКС() найдем минимальное и максимальное значения выборки:

Далее посчитаем частоты, для этого разобьем выборку на пять интервалов одинаковой длины. Для того, чтобы узнать шаг
 , воспользуемся формулой:
, воспользуемся формулой: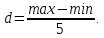

Для подсчета частот построим таблицу:

В этой таблице в шапке указаны границы интервалов, от минимального до максимального значений выборки с шагом
 , в нижней строке укажем количество значений, попавших в каждый интервал:
, в нижней строке укажем количество значений, попавших в каждый интервал:
Для удобства, значения, попавшие в одинаковый интервал, выделены одним цветом.
Найдем относительные частоты:

Выполним контроль: сумма частот должна быть равна объему выборки, а сумма относительных частот единице:

Используя формулы, вычислим выборочное среднее:
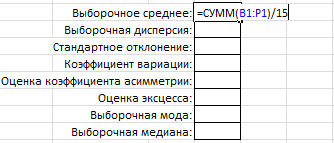
В диапазоне ячеек B1:P1 находится выборка.
Выборочную дисперсию:
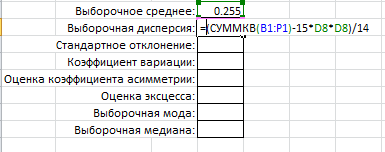
Ячейка D8 – это значение выборочного среднего.
Среднее квадратическое отклонение:
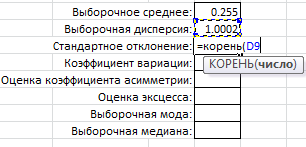
D9 – ссылка на ячейку, в которой находится значение дисперсии.
Далее вычислим коэффициент вариации, разделив среднее квадратическое отклонение на выборочное среднее:

Для расчета значений коэффициентов асимметрии и эксцесса нам потребуются значения центральных моментов второго, третьего и четвертого порядков. Для этого для каждого элемента выборки найдем его разность с выборочным средним:
В ячейке D8 находится выборочное среднее. Затем возведем каждую разность во вторую, в третью и в четвертую степени:

Найдем сумму значений в каждой строке и разделим на объем выборки:

Полученные значения и есть центральные моменты второго, третьего и четвертого порядка:

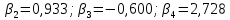 .
.
Вычислим асимметрию:
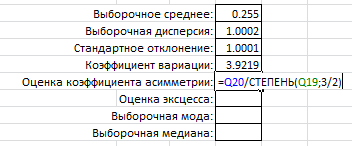
Здесь в ячейке Q20 – значение центрального момента третьего порядка, а в ячейке Q19 – значение центрального момента второго порядка.
Для оценки эксцесса наберем формулу:

В ячейке Q21 значение центрального момента четвертого порядка.
Далее вычислим моду и медиану. Для расчета моды потребуется интервал с максимальной частотой. В нашем случае
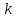 =4, тогда
=4, тогда 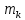 =7,
=7, 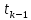 = 0,312,
= 0,312, 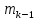 =3,
=3, 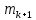 =2. Наберем формулу:
=2. Наберем формулу: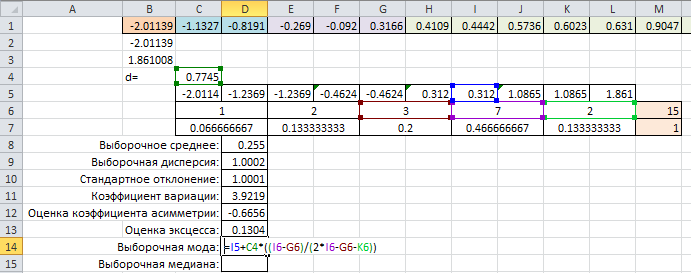
Наконец, для расчета медианы определим интервал, удовлетворяющий условиям:
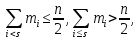
то есть, нужно найти такой интервал, в котором сумма частот превышает половину объема выборки. В нашем случае номер такого интервала
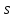 =4, так как на третьем интервале сумма частот меньше половины объема выборки:
=4, так как на третьем интервале сумма частот меньше половины объема выборки: 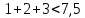 , а на четвертом интервале
, а на четвертом интервале 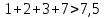 . Тогда
. Тогда 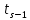 =0,312,
=0,312, 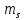 =7,
=7, 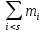 =1+2+3=6,
=1+2+3=6, 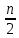 =15/2=7,5,
=15/2=7,5,  =0,774. Наберем формулу:
=0,774. Наберем формулу: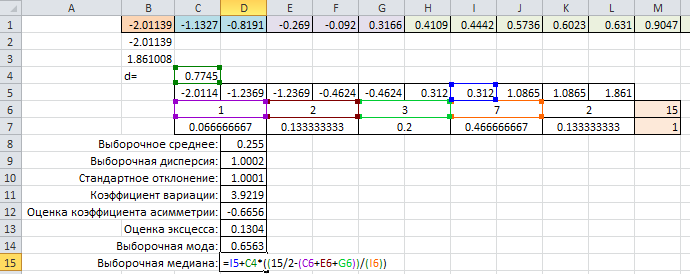
Окончательно получим значения основных числовых характеристик:
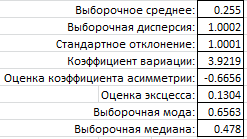
Выполним предварительную проверку на нормальность.
1. Рассчитаем границы интервалов
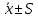 ,
,  и
и 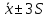 :
:
В ячейке D8 находится значение выборочного среднего, в ячейке D10 значение среднего квадратического отклонения. Посчитаем, сколько значений выборки попадает в образованные интервалы:

В последнем столбце указаны процентные соотношения полученных значений от объема выборки. Полученные значения позволяют говорить о том, что по первому критерию выборка является нормальной.
2. Оценка эксцесса
 и коэффициента асимметрии
и коэффициента асимметрии 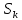 ‚ должны быть близки к нулю; Значение эксцесса
‚ должны быть близки к нулю; Значение эксцесса  =0,134, значение коэффициента асимметрии
=0,134, значение коэффициента асимметрии 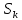 =-0,665. Эти значения достаточно малы, чтобы принять их незначимо отличными от нуля.
=-0,665. Эти значения достаточно малы, чтобы принять их незначимо отличными от нуля. 3.
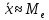 , в нашем случае
, в нашем случае 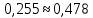 .
.Учитывая все три критерия, можно говорить о том, что выборка является нормальной.
Наконец, используя средства построения графиков Excel, построим гистограмму и полигон частот:
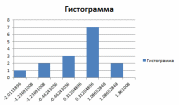 | 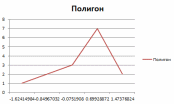 |
