Программа среднего профессионального образования

44.02.04 Специальное дошкольное образование

Дисциплина: Математика

Практическое занятие 2


Выполнил:

Обучающийся Власенко Ирина Андреевна

Преподаватель:

Сазонова Элеонора Борисовна


Цель занятия: формирование умений решать текстовые задачи; применять математические методы для решения профессиональных задач; закрепление навыков решения простейших статистических задач; закрепление навыков применять правила приближенных вычислений; закрепление навыков работы с основными свойствами геометрических фигур на плоскости и в пространстве.

 

Задание 1. (Максимальное количество баллов – 3 балла)

Таблица – «Виды моделирования при решении текстовых задач»

В таблице «Виды моделирования при решении текстовых задач» заполните позицию «Необходимо определить» в графе «Интерпретация модели».

Задача	Модель	Интерпретация модели
1.     1. Было 7 кубиков, проиграно 4 кубика. Сколько кубиков осталось?		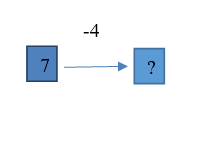Пример ответа: Известно: начальное состояние объекта; направленность отношения между начальным и конечным состоянием объекта; числовое значение величины отношения между состояниями объекта. Необходимо определить числовое значение величины конечного состояния объекта.
2. Было 4 кубика, стало 7 кубиков. Что произошло?		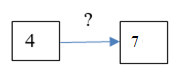Известно: начальное и конечное состояние объекта; направленность отношения между ними. Необходимо определить числовое значение величины отношения между состояниями объекта.

---

3. Имеется 7 кубиков после того, как добавили 4 кубика. Сколько кубиков было до добавления?		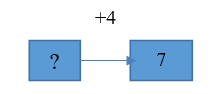Известно: значение величины конечного состояния объекта, направленность отношений между состояниями объекта и числовое значение величины отношений между состояниями объектов. Необходимо определить значение величины начального состояния объекта
4.Было 7 кубиков, стало 4 кубика. Что произошло?		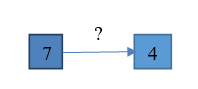Известно: значение величины начального и конечного состояния объекта, направленность отношений между состояниями объекта. Необходимо определить числовое значение величины отношений между состояниями объектов
5.В первый раз принесли 7 кубиков, во второй раз – забрали 4 кубика. Что произошло в результате?		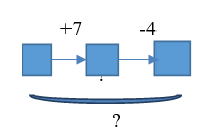Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта (начального, промежуточного и конечного). Необходимо определить числовое значение величины отношений между начальным и конечным состояниями объектов

6. В первый раз забрали 7 кубиков, во второй – принесли 4 кубика. Что произошло в результате?		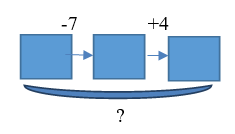Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта. (начального, промежуточного и конечного). Необходимо определить числовое значение величины отношений между начальным и конечным состояниями объектов
7.В первый раз забрали 4 кубика. После того, как кубики забрали второй раз, всего было отдано 7 кубиков. Что произошло во второй раз?		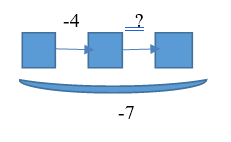Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта (начальным и промежуточным; начальным и конечным) Необходимо определить числовое значение величины отношений между промежуточным и конечным состояниями объектов
8. В первый раз забрали 7 кубиков. После того, как во второй раз принесли кубики, оказалось, что всего было отдано 4 кубика. Что произошло во второй раз?		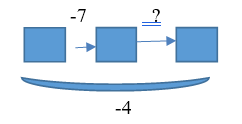Известно: направленность отношений между состояниями объекта; значение величин отношений между начальным и промежуточным, между промежуточным и конечным состоянием объекта. Необходимо определить числовое значение величины отношений между промежуточным и конечным состояниями объектов

---

Задание 2. (Максимальное количество баллов – 3 балла)

 Используя диаграммы Эйлера-Венна решить задачу.

При выборе кружков для детей оказалось, что 60% родителей желают, чтобы их ребенок посещал кружок рисования, 50% предпочли занятия по гимнастике, 50% отметили, что выбрали бы занятия музыкой. При этом 30% родителей предпочитают, чтобы их дети посещали занятия и по рисованию, и по гимнастике, 20% – сделали выбор в пользу занятий по гимнастике и музыке, а 40% родителей –  пожелали бы, чтобы ребенок рисовал и занимался хоровым пением, и только 10% из них выразили свое мнение за посещение детьми всех кружков. Определите процентное соотношение родителей, которые:

1) не желают водить детей в кружки;

2) выбрали не менее двух кружков.

Решение

В задаче речь идет о трех множествах:

Р – «родители, которые предпочли занятия по рисованию»

Г – «родители, которые предпочли занятия по гимнастике»

М – «родители, которые предпочли занятия по музыке (хоровое пение)» 

U – универсальное множество (все родители, выбирающие кружки)



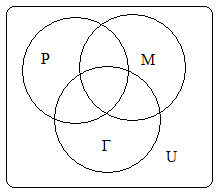
Известны следующие данные:

|U|=100% |Р|=60%, |Г|=50%, |М|=50%, |Р 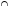Г|=30%, |Г 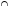М|=20%,

|Р 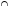М|=40%, | Р 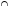М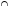 Г|= 10%

Разметим диаграмму так, чтобы каждый родитель в ней участвовал только один раз. Т.е. определим мощности каждой из областей диаграммы.

1) Все три кружка: | Р 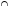М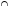 Г|= 10%

2) Только рисование и гимнастика: |Р 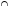Г|-| Р 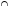М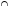 Г|=30%-10%=20%

3) Только рисование и музыка: |Р 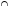M|-| Р 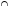М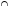 Г|=40%-10%=30%

4) Только гимнастика и музыка: |Г 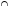M|-| Р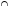

---

М 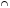Г|=20%-10%=10%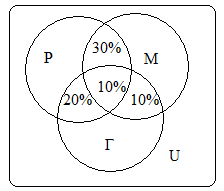



5) Только рисование: 60%-(30%+20%+10%)=0%

6) Только гимнастика: 50%-(20%+10%+10%)=10%

7) Только музыка: 50%-(30%+10%+10%)=0%



Значит |Р Г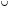 М|=0%+10%+0%+30%+20%+10%+10%=80%

Получаем ответы:

Не желают водить детей в кружки: 100%-80%=20%

Выбрали не менее двух кружков: 30%+20%+10%+10%=70%
Ответ: 1) 20%; 2) 70%

Задание 3. (максимальное количество баллов – 5 баллов)

При измерении получены данные:

Номер измерения	1	2	3	4	5	6	7	8	9	10
Данные	20	20	5	10	10	15	20	5	5	20

Выполните задания с учетом исходных данных, подробно описывая ход решения.

a) Построить статистический ряд распределения частот.

b) Построить полигон распределения.

c) Вычислить выборочную среднюю, дисперсию, моду, медиану.

d) Построить выборочную функцию распределения.
Решение

Отсортируем данные в порядке неубывания, получим вариационный ряд

1	2	3	4	5	6	7	8	9	10
5	5	5	10	10	15	20	20	20	20

---

Строим статистический ряд распределения частот. Для каждого возможного значения выписываем частоту появления

xi	5	10	15	20
ni	3	2	1	4

Полигон распределения


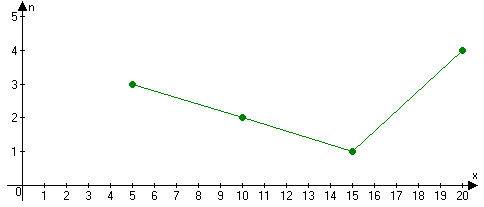
Выборочное среднее:

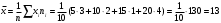
Дисперсия



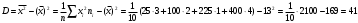
Мода

Наибольшая частота равна 4, ей соответствует значение 20, поэтому Мо=20

Медиана

1	2	3	4	5	6	7	8	9	10
5	5	5	10	10	15	20	20	20	20

Всего 10 вариант (четное число), поэтому, медиана:



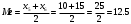
Строим статистический ряд распределения относительных частот

xi	5	10	15	20
ni/10	0,3	0,2	0,1	0,4

Построим выборочную функцию распределения.



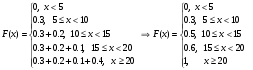
График:



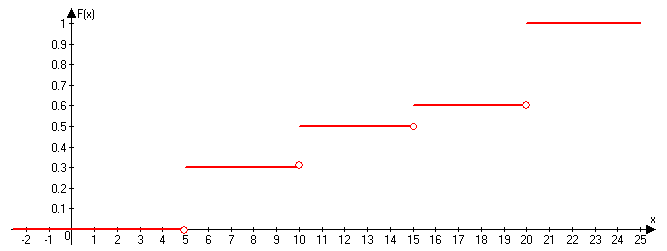
Задание 4. (максимальное количество баллов - 4 балла)

---

Смотрите также файлы

• Программа среднего профессионального образования 44. 02. 01 Дошкольное образование Дисциплина Родной язык Практическое занятие 2.doc

• Разработка программы расчета энергоснабжения дома.docx

• Тесты по литературе для i курса i вариант о каком персонаже Грозы.doc

• Ошибки в доказательстве. Софизмы.doc

• 1. Политическая элита российского общества.docx