Решите примеры, связанные с погрешностями, подробно описывая ход решения.

a) Округлить число 4,45575250 до шести, пяти, четырех, трех, двух и одного десятичных знаков; до целого числа.

b) Число 12,75 определено с относительной погрешностью 0,3, %. Найдите абсолютную погрешность округления.

c) Определите верные и сомнительные цифры числа 13,27 ± 0,03.

 Решение

а) число 4,45575250

Округляем до шести десятичных знаков: шестой десятичный знак равен 2, седьмой десятичный знак равен 5. Т.к. 5 5, то прибавляем к числу 2 единицу и отсекаем остальные цифры (округляем в большую сторону), получаем: 4,455753

Округляем до пяти десятичных знаков: пятый десятичный знак равен 5, седьмой десятичный знак равен 2. Т.к. 2<5, то просто отсекаем остальные цифры (округляем в меньшую сторону), получаем: 4,45575

Округляем до четырех десятичных знаков: четвертый десятичный знак равен 7, пятый десятичный знак равен 5. Т.к. 5 5, то прибавляем к числу 7 единицу и отсекаем остальные цифры (округляем в большую сторону), получаем: 4,4558

Округляем до трех десятичных знаков: третий десятичный знак равен 5, четвертый десятичный знак равен 7. Т.к. 7 5, то прибавляем к числу 5 единицу и отсекаем остальные цифры (округляем в большую сторону), получаем: 4,456

Округляем до двух десятичных знаков: второй десятичный знак равен 5, третий десятичный знак равен 5. Т.к. 5 5, то прибавляем к числу 5 единицу и отсекаем остальные цифры (округляем в большую сторону), получаем: 4,46

Округляем до одного десятичного знака: первый десятичный знак равен 4, третий десятичный знак равен 5. Т.к. 5 5, то прибавляем к числу 4 единицу и отсекаем остальные цифры (округляем в большую сторону), получаем: 4,5

Округляем до целого числа: целая часть равна 4, первый десятичный знак равен 4. Т.к. 4<5, то просто отсекаем дробную часть (округляем в меньшую сторону), получаем: 4

b) Число x=12,75 определено с относительной погрешностью 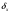=0,3%. Найдем абсолютную погрешность 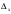округления.

Абсолютная погрешность измеряемой величины равна разности измеренного х и истинного значения Х, которое неизвестно:

---

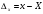
Отсюда получим истинное значение

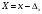
Относительная погрешность 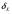равна отношению абсолютной погрешности к истинному значению измеряемой величины: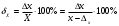

Отсюда получаем:



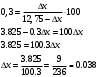
Ответ:

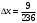
c) Определим верные и сомнительные цифры числа 13,27 ± 0,03.

Цифра называется верной, если граница абсолютной погрешности данного приближенного значения числа не больше единицы того разряда, в котором записана эта цифра. В противном случае цифра называется сомнительной.

Граница абсолютной погрешности равна 0,03

Единица последнего разряда - 0,01 (сотые), имеем: 0,03>0,01, значит, цифра 7 является сомнительной.

0,03<0,1 (десятые), значит, цифра 2 является верной

0,03<1(единицы), значит, цифра 3 является верной

0,03<10 (десятки), значит, цифра 1 является верной

Последние два вычисления можно было не производить, т.к. если в записи приближенного значения числа какая-то цифра – верная, то и все предшествующие ей цифры так же являются верными.

Ответ: верные цифры: 1,3,2; сомнительная - 7

Задание 5. (максимальное количество баллов – 3 балла)

 Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением.

На стороне AC треугольника ABC отмечена точка D так, что AD=3см, DC=10см. Площадь треугольника ABC равна 39 см². Найдите площадь треугольника ABD.

Решение

Построим треугольник и отметим известные данные



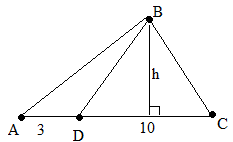
Известно, что площадь треугольника ABC равна 39 см²

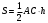, где h – высота треугольника, опушенная из вершины В

Длина основания известна: AC=AD+DC=3см+10см=13 см. Значит, можем найти длину высоты h: 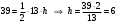см

Высота h так же является высотой треугольника ABD (опущена из той же точки B на ту же прямую AC, потому что AD и АС лежат на одной прямой). Значит, можем найти площадь треугольника ABD: 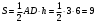см²

Ответ: 9 см²

Задание 6. (максимальное количество баллов – 4 балла)

---

 Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением.

Биссектриса угла A параллелограмма ABCD пересекает его сторону BC в точке F. Найдите площадь параллелограмма ABCD, если BF=4 см, FC=2 см, а угол ABC равен 150⁰.

Решение

Построим параллелограмм и отметим известные данные



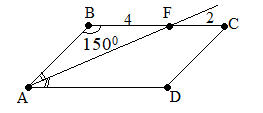
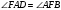как накрест лежащие при параллельных прямых ВС, AD и секущей AF. Т.к. AF – биссектриса угла А, то 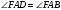. Следовательно .

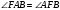Отсюда следует, что треугольник ABF равнобедренный, значит АВ=BF=4.

Находим площадь параллелограмма:

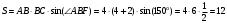см²

Ответ: 12 см²

 

Задание 7. (максимальное количество баллов – 3 балла)

 Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением.

Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6см и 8см, а боковое ребро призмы равно 12см.

Решение

Построим прямую призму и отметим известные данные



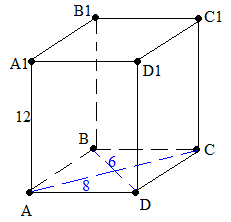
Найдем сторону ромба, лежащего в основании, через длины его диагоналей:



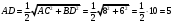
Найдем площадь ромба, лежащего в основании, через длины его диагоналей:



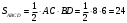
Находим площадь боковой поверхности, которая состоит из четырех прямоугольников со сторонами 5 и 1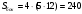2: см²

Значит, площадь полной поверхности (боковая плюс два ромба):

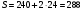см²

Ответ: 288 см²

10>

---

Смотрите также файлы

• Программа среднего профессионального образования 44. 02. 01 Дошкольное образование Дисциплина Родной язык Практическое занятие 2.doc

• Разработка программы расчета энергоснабжения дома.docx

• Тесты по литературе для i курса i вариант о каком персонаже Грозы.doc

• Ошибки в доказательстве. Софизмы.doc

• 1. Политическая элита российского общества.docx