1. Роль цифровой техники в современных электронных системах, цифровые и импульсные сигналы, их параметры

ответ

Люди ежедневно пользуются техникой для выполнения конкретных задач или развлечения. Современные или эволюционировавшие технологии иногда могут заменить ранее использовавшиеся из-за их возросших преимуществ или новообретенной популярности. Возьмем, к примеру, транспортную технологию; когда-то широко использовались паровые поезда, а теперь их заменили электропоездами, которые двигаются значительно быстрее, что позволяет более эффективно использовать время и бережнее использовать природные ресурсы.

И 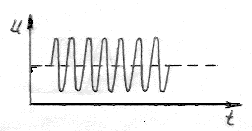мпульсный сигнал (электрический импульс) - кратковременное изменение напряжения или тока в электрической цепи, соизмеримое с переходным периодом в этой цепи.

Классификация импульсных сигналов: · радиоимпульсы;· видеоимпульсы.

название цифровых сигналов — дискретные Довольно часто встречается термин дискретные состояния Цифровые сигналы изменяются от одного дискретного состояния к другому почти мгновенно, не останавливаясь в промежуточных состояниях.

Примером цифрового сигнала могут служить показания новейшего цифрового спидометра в автомобиле (сравните с примером аналогового спидометра в предыду­щем разделе). Когда скорость автомобиля увеличивается, цифры, показывающие зна­чение скорости в километрах в час,

2. Основные понятия, позиционные и непозиционные системы счисления, основные системы счисления, правила перевода из одной системы в другую.

ответ

Система счисления (далее СС) - совокупность приёмов и правил для записи чисел цифровыми знаками.

Наиболее известна десятичная СС, в которой для записи чисел используются цифры 0,1,:,9. Способов записи чисел цифровыми знаками существует бесчисленное множество. Любая предназначенная для практического применения СС должна обеспечивать:

· возможность представления любого числа в рассматриваемом диапазоне величин;

· единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина);

· простоту оперирования числами; Название Цифры двоичная 0,1 троичная 0,1,2 восьмеричная 0,...,7

шестнадцатеричная 0,...,9,A, ...,F

Непозиционной системой называется такая, в которой количественное значение каждой цифры не зависит от занимаемой ей позиции в изображении числа (римская система счисления).

---

Позиционной системой счисления называется такая, в которой количественное значение каждой цифры зависит от её позиции в числе (арабская система счисления). Количество знаков или символов, используемых для изображения числа, называется основанием системы счисления.

Позиционные системы счисления имеют ряд преимуществ перед непозиционными: удобство выполнения арифметических и логических операций, а также представление больших чисел, поэтому в цифровой технике применяются позиционные системы счисления

3. Системы счисления: двоичная, двоично-десятичная, восьмеричная, шестнадцатиричная.

ответ



4. Представление чисел в форме с плавающей запятой, представление чисел в форме с фиксированной запятой. Кодирование чисел.

ответ

В форме представления с фиксированной запятой все числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, от­деляющей целую часть от дробной.

Например: в десятичной системе счисления имеется 5 разрядов в целой части чи­сла (до запятой) и 5 разрядов в дробной части числа (после запятой); числа, запи­санные в такую разрядную сетку, имеют вид:

+00721,35500; +00000,000328; -10301,20260.

В форме представления с плавающей запятой каждое число изображается в виде двух групп цифр. Первая группа цифр называется мантиссой, вторая – порядком, причем абсолютная величина мантиссы должна быть меньше 1, а порядок – це­лым числом. В общем виде, число в форме с плавающей запятой может быть пред­ставлено так:

N = ±M·P±r, где М – мантисса числа (|М| < 1 ); r – порядок числа (r – целое число); Р – основа­ние системы счисления. Например, приведенные ранее числа в нормальной форме запишутся так: +0,721355·103; +0,328·10-3; -0,103012026·105.

5. Арифметические действия над числами. Прямой, обратный и дополнительный код.

о 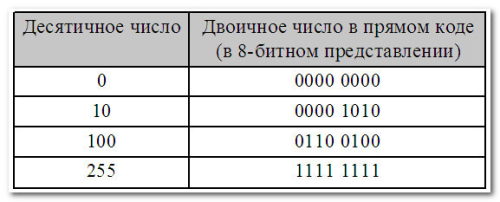тветВ первом (основной) - для записи только неотрицательных чисел:

Обратный код - метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения.

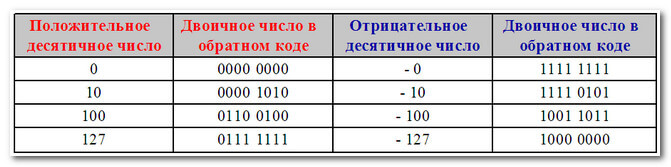
Обратный двоичный код положительного числа состоит из одноразрядного кода знака (битового знака) - двоичной цифры 0, за которым следует значение числа.

Обратный двоичный код отрицательного числа состоит из одноразрядного кода знака (битового знака) - двоичной цифры 1, за которым следует инвертированное значение положительного числа.

---

Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.

Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).

Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.

восмеричный сс



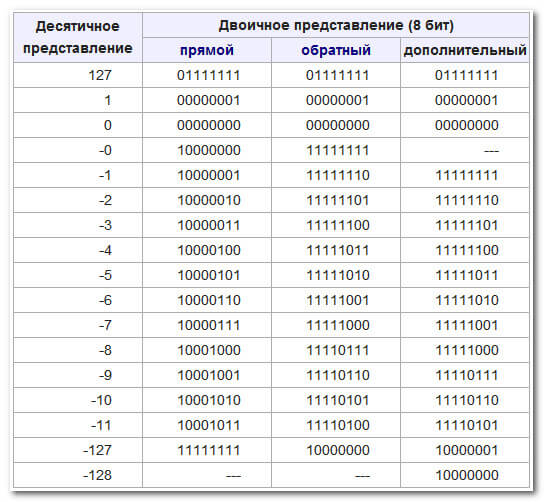
Дополнительный код - наиболее распространенный способ представления отрицательных чисел. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел.

В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).



6.Общие сведения, основные понятия алгебры логики. Основные переключательные функции, тождества и законы алгебры логики.

ответ

При проектировании ЭВМ значительное внимание уделяют выбору операционных блоков для реализации заданных логических и арифметических операций. Преобразование информации в ЭВМ производится электронными логическими схемами двух типов: комбинационными схемами и цифровыми автоматами. Комбинационные схемы – устройства, выходной сигнал которых зависят только от комбинации входных сигналов. В них отсутствуют элементы памяти, и они не способны сохранять выходное значение. Цифровые автоматы – в отличие от комбинационных схем в них результат преобразования информации зависит не только от входных значений, но и от внутреннего состояния. Для сохранения внутреннего состояния в них содержатся элементы памяти. Работа цифровых устройств лучше всего математически описывается алгеброй логики или булевой алгеброй. В алгебре логики операции выполняются над логическими высказываниями. Под высказыванием понимают любое утверждение, в отношении которого имеет место утверждать, истинно оно или ложно. Высказывания могут быть простые и сложные. Простые высказывания называют переменными и обозначают большими буквами (A, B, C). Сложные высказывания называют функциями и обозначают строчными буквами (f ,k). Логические переменные и функции могут иметь только два значения 0 – ложное, 1 – истинное. В ЭВМ для представления логических переменных используют двухпозиционные электронные элементы. Построение логических схем в ЭВМ осуществляется на основе переключательной функции, записанной в аналитической форме. Наиболее наглядной формой задания переключательной функции является таблица истинности, отражающая значения функции при всевозможных комбинациях значений переменных. Булевая алгебра базируется на основе трех логических функций

---

7. Дизъюнктивная, конъюнктивная нормальные формы представления СДНФ и СКНФ. Понятие минтерма, макстерма. Привести примеры.

Конъюнктивным одночленом (элементарной конъюнкцией) от переменных называется конъюнкция этих переменных или их отрицаний.

Например, элементарная конъюнкция.

Дизъюнктивным одночленом (элементарной дизъюнкцией) от переменных называется дизъюнкция этих переменных или их отрицаний.

Например, элементарнаядизъюнкция.

Формула, равносильная данной формуле алгебры высказываний и являющаяся дизъюнкцией элементарных конъюнктивных одночленов, называется дизъюнктивной нормальной формой (ДНФ) данной формулы.

Например ,сДНФ.

Определение 4. Формула, равносильная данной формуле алгебры высказываний и являющаяся конъюнкцией элементарных дизъюнктивных одночленов, называется конъюнктивной нормальной формой (КНФ) данной формулы.

Например, сКНФ
Макстерм (H) или дизъюнктивный терм (ИЛИ) – это ЛФ, связывающая все переменные в прямой и инверсной форме (литералы) знаком дизъюнкции. Конституента нуля (K0) тождественна макстерму.

Элементарная сумма – это дизъюнкция нескольких переменных или их отрицаний – макстерм (ИЛИ).

Минтерм (F) или конъюнктивный терм (И) – это ЛФ, связывающая все переменные в прямой и инверсной форме (литералы) знаком конъюнкции. Конституента единицы (K1) тождественна минтерму.

Элементарное произведение – это конъюнкция нескольких переменных или их отрицаний – минтерм (И).

8. Минимизация переключательных функции любой сложности. Карты Карно. Привести примеры.

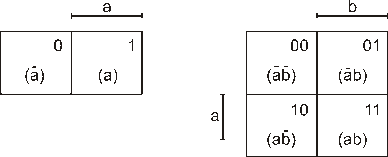
При решении задач минимизации как полностью определенных, так и не полностью определенных переключательных функций, зависящих от небольшого числа переменных, широкое применение находят графические методы. Карта Карно – это таблица истинности специального вида, в которой переменные функции расположены не одномерным, а двумерным массивом (по горизонтали и вертикали), причем каждому набору переменных поставлена в соответствие одна клетка. В эту клетку записывается значение функции (0 или 1) на данном наборе

---

.

9. Этапы синтеза комбинационных схем. Правила оформления схем цифровых устройств. Понятие базиса. Привести примеры.

ответ

Синтез комбинационных схем включает в себя четыре этапа:

1. 
   постановка задачи
   
2. 
   составление таблицы истинности, в которой отражена заданная функция при соответствующих сочетаниях переменных
   
3. 
   составление СДНФ (СКФН) на основе таблицы истинности и упрощение полученного выражения
   
4. 
   построение схемы с учетом оптимального набора элементов
   

Электрические схемы для изделий цифровой техники требуется выполнять] согласно ГОСТ 2.708-81 и с учетом требований согласно ГОСТ 2.702-75, ГОСТ 2.751-73, ГОСТ 2.710-81.

Определение. Три линейно независимых вектора , и образуют в пространстве базис, если любой вектор может быть представлен в виде некоторой линейной комбинации векторов , и , т.е. если для вектора найдутся такие вещественные числа , , , что справедливо равенство: =++ (1)

Определение. Два лежащих в плоскости  линейно независимых вектора и образуют на этой плоскости базис, если любой лежащий в плоскости  вектор может быть представлен в виде некоторой линейной комбинации векторов и , т.е. если для любого лежащего в плоскости  вектора найдутся такие вещественные числа  и , что справедливо равенство : =+

Утверждения.

1) любая тройка некомпланарных векторов , и образует базис в пространстве;

2) любая пара лежащих в данной плоскости неколлинеарных векторов и образует базис на этой плоскости.

10. Анализ и синтез комбинационных схем в различных базисах. Примеры.

ответ

Техническим аналогом булевой функции в вычислительной технике является, так называемая, комбинационная схема, на вход которой поступают и с выхода снимаются электрические сигналы в виде одного из уровней напряжения, соответствующих значениям логического 0 и логической 1. Для выяснения, что же такое комбинационная схема, рассмотрим схему S, имеющую mвходов иnвыходов (рис. 1). На её входы могут быть поданы наборы значений входных переменныхXi{0,1},, а на выходах формируются выходные переменныеYj{0,1},.

С 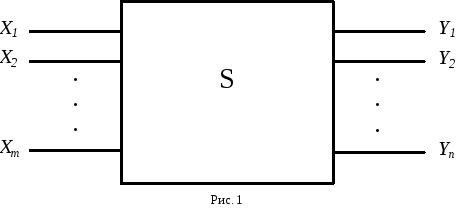хема S называется комбинационной, если каждую изnфункций её выходовY1,Y2, ..., Ynможно представить как булеву функцию входных переменныхX1, X2, ..., Xm.

---

Смотрите также файлы

• Унитарное или Федеративное.docx

• Тема Процессы и инструменты управления проектами системный подход Смоделируйте процесс Инициализация проекта.docx

• Дисциплина Основы управления образовательной организацией Практическое задание 3, Модуль 3.doc

• Ковалёвой Лилии Олеговны курс 2 группа 3 Форма обучения заочная предметы ухода за больными и правила пользования.doc

• Вариант Вопрос Парафиновые, нафтеновые и ароматические углеводороды. Парафиновые углеводороды.docx