Файл: Контрольная работа по дисциплине Теория игр.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 05.05.2024

Просмотров: 14

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Новосибирский государственный технический университет»
КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Теория игр»

Выполнил:

студент гр. ДЭ-900

Аббасова Е. Б.

шифр143310801
Проверил:

преподаватель

Джафаров К.А.

Новосибирск

2021
Вариант 1


  1. Бомбить аэродром отправляются 3 самолета, 2 из них – бомбардировщики. Противник может выстрелить по двум самолетам. При выстреле по самолету он поражает летящий первым с вероятностью 0,4, летящий вторым или третьим – с вероятностью 0,5. Аэродром разбомблен, если хотя бы один бомбардировщик уцелел. Сформулировать задачу как задачу теории игр. Найдите решение или укажите алгоритм нахождения решения.


Решение:

Формализуем игру и составим матрицу.

Цель А – сбить все бомбардировщики выстрелом по 2-м самолетам. Цель В – разбомбить аэродром, сохранив при этом как минимум 1 бомбардировщик. Вероятность поражения самолета, летящего первым – наименьшая из всех представленных, поэтому игрок В будет стремиться направить первым бомбардировщик, а порядок пролета 2-х следующих безразличен. Элемент Вi – вид самолета, Аi – выстрел по самолету.

Представим игровую матрицу:
В1
В2
В3

А1
0
0,5
0,5

А2
0,4
0,5
0

А3
0,4
0
0,5


Решение:

Найдем нижнюю и верхнюю цену игры
B1
B2
B3
a = min(Ai)

A1
0
0,5
0,5
0

A2
0,4
0,5
0
0

A3
0,4
0
0,5
0

b = max(Bi)
0,4
0,5
0,5




Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = 0, которая указывает на максимальную чистую стратегию A1.

Верхняя цена игры b = min(bj) = 0,4.

Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах 0 ≤ y ≤ 0,4. Находим решение игры в смешанных стратегиях. Объясняется это тем, что игроки не могут объявить противнику свои чистые стратегии: им следует скрывать свои действия. Игру можно решить, если позволить игрокам выбирать свои стратегии случайным образом (смешивать чистые стратегии).

Находим решение игры в смешанных стратегиях.

Запишем систему уравнений.

Для игрока I

0,4p2+0,4p3= y

0,5p1+0,5p2= y

0,5p1+0,5p3= y

p1+p2+p3= 1

Для игрока II

0,5q2+0,5q3= y

0,4q1+0,5q2= y

0,4q1+0,5q3= y

q1+q2+q3= 1

Решая эти системы методом Гаусса, находим:

y = 0,308

p1= 0,231 (вероятность применения 1-ой стратегии).

p2= 0,385 (вероятность применения 2-ой стратегии).

p3= 0,385 (вероятность применения 3-ой стратегии).

Оптимальная смешанная стратегия игрока I: P = (0,231; 0,385; 0,385)

q1= 0,385 (вероятность применения 1-ой стратегии).

q2= 0,308 (вероятность применения 2-ой стратегии).

q3= 0,308 (вероятность применения 3-ой стратегии).

Оптимальная смешанная стратегия игрока II: Q = (0,385; 0,308; 0,308)

Цена игры:

y = 0,308


  1. Рассмотреть игру с матрицей потерь первого игрока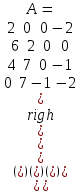 . Ответьте на вопросы: а) есть ли цена в простой игре; если есть , то найдите оптимальные стратегии игроков; б) если цены нет, то составьте системы уравнений для нахождения решения этой игры; в) найдите оптимальную стратегию первого игрока по критерию Гурвица.


Решение:

А) Найдем цену игры, если таковая имеется:

Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях.
B1
B2
B3
B4
a = min(Ai)

A1
2
0
0
-2
-2

A2
6
2
0
0
0

A3
4
7
0
-1
-1

A4
0
7
-1
-2
-2

b = max(Bi)
6
7
0
0




Находим нижнюю цену игры a = max(ai) = 0, которая указывает на максимальную чистую стратегию A2.

Верхняя цена игры b = min(bj) = 0.

Седловая точка (2, 3) указывает на стратегии игроков (A2,B3). Цена игры равна 0.

В) Найдем оптимальную стратегию первого игрока по критерию гурвица

Считаем, что в данном случае необходимо минимизировать риск. Примем критерий оптимизма-пессимизма равным 0,5

Поскольку необходимо минимизировать затраты, то модифицируем матрицу умножением всех элементов на (-1) и затем сложением их с максимальным элементом матрицы (7) так, чтобы матрица не содержала бы отрицательных элементов. Тем самым сводим решение к поиску максимальной функции.





В1
В2
В3
В4

А1
5
7
7
9

А2
1
5
7
7

А3
3
0
7
8

А4
7
0
8
9


si= y min(aij) + (1-y)max(aij)

Рассчитываем si.

s1= 0,5*5+(1-0,5)*9 = 7

s2= 0,5*1+(1-0,5)*7 = 4

s3= 0,5*0+(1-0,5)*8 = 4

s4= 0,5*0+(1-0,5)*9 = 4,5

Ai
П1
П2
П3
П4
min(aij)
max(aij)
y min(aij) + (1-y)max(aij)

A1
5
7
7
9
5
9
7

A2
1
5
7
7
1
7
4

A3
3
0
7
8
0
8
4

A4
7
0
8
9
0
9
4,5


Выбираем максимальный элемент max=7

Таким образом, выбираем стратегию A1.



  1. Рассмотреть бескоалиционную биматричную игру со следующей матрицей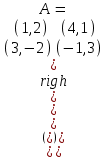 . Найдите все ситуации равновесия.


Решение:

Найдем ситуации равновесия по Нэшу, для этого выделим в каждом столбце первой матрицы максимальный элемент, в каждой строке максимальный элемент второй матрицы:


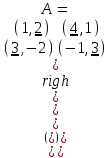
Подчеркнутые элементы матриц, стоящие в одном положении матриц определяют ситуации равновесия по Нэшу.

Если биматричная игра не имеет равновесных ситуаций в чистых стратегиях, то она неразрешима в чистых стратегиях. И тогда можно искать решение в смешанных стратегиях.

Итак, чтобы в биматричной игре:

А=(a), В = (b) пара (p,q);

определяемая равновесную ситуацию, необходимо и достаточно одновременное выполнение следующих неравенств:

(p–1)(Cq-α) ≥ 0, p(Cq-α) ≥ 0; 0 ≤ p ≤ 1

(q-1)(Dp-β) ≥ 0, q(Dp-β) ≥ 0; 0 ≤ q ≤ 1

где

C = a11 - a12 - a21 + a22

α = a22- a12 

D = b11-b12-b21+b22 

β = b22-b21 

Проводя необходимые вычисления: 

C = 1 - 4 - 3 -1 = -7 

α = -1 - 4 = -5 

D = 2 - 1 - (-2) + 3 = 6 

β = 3 - (-2) = 5 

и рассуждения 

(p–1)(-7q+5) ≥ 0 

p(-7q+5) ≥ 0

(q-1)(6p-5) ≥ 0

q(6p-5) ≥ 0

получаем, что:

p=1,q ≤ 5/7

p=0, q ≥ 5/7 

0 ≤ p ≤ 1, q=5/7

2) q=1,p ≥ 5/6

q=0, p ≤ 5/6 

0 ≤ q ≤ 1, p=5/6 

Рассматриваемая игра имеет единственную ситуацию равновесия (P*,Q*), где оптимальными стратегиями по Нэшу являются: 

P* = (5/6;1/6); Q* = (5/7;2/7). 

Смотрите также файлы