Файл: Контрольная работа по дисциплине Численные методы.doc

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ) ДГТУ в г. Азове

Контрольная работа

по дисциплине «Численные методы»

Выполнил: студент гр. ЗИСS-21

Шифр 2161288

Шеменев М.В.
Проверил: Чумак И.В.

Азов

2023 г

Содержание

Задание 1. Погрешности источники их возникновения. Правила вычисления погрешностей. 3

Задание 2. Численное решение уравнений. 5

Задание 3. Интерполирование математических таблиц. 8

Задание 4. Вычисление интегралов при помощи формул Ньютона-Котеса. 10

Задание 5. Нахождение решений обыкновенных дифференциальных уравнений и систем дифференциальных уравнений при помощи формул Эйлера и Рунге – Кутта. 11

Используемая литература. 15

Задание 1. Погрешности источники их возникновения. Правила вычисления погрешностей.

Пусть а, b, у — приближенные числа с верными в строгом смысле значащими цифрами, х — точное число. Вычислите


и оцените погрешность результата. Для вычисления значений функций sin у используйте либо микрокалькулятор, либо компьютер.

Вариант	a	b	x	y
16	2,88	3,568	6,12	1,23

Вычислим абсолютную и относительную погрешности исходных данных.

При помощи Excel заполним первую таблицу, определим абсолютные погрешности исходных данных по известным верным значащим цифрам.


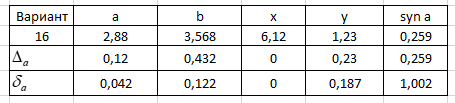
Рисунок 1.1 – Таблица с входными данными.

---

Рисунок 1.2 – Просмотр таблицы в виде формул.
Разобьем заданное выражение на простые действия и вычислим погрешности арифметических операций. Оценим погрешность z1 = ab, для этого возьмем три значащие цифры произведения. Затем найдем верные значащие цифры z1 и запишем ответ с одной сомнительной цифрой. Аналогично вычислим z2, z3, z4, z.


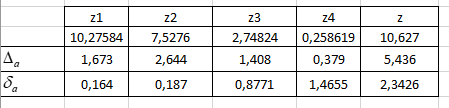
Рисунок 1.3 – Таблица вычислений.


Рисунок 1.4 – Просмотр таблицы вычисления в виде формулы.
Вывод: приближенное значение заданной функции равняется 10,627, относительная погрешность 5,436, абсолютная погрешность 2,3426, следовательно верные значащие цифры результата: 10,6,2.

Задание 2. Численное решение уравнений.

Отделите корни уравнения и выберите один из отрезков изоляции, на котором выполняются условия применимости методов указанных в вашем варианте:

1) половинного деления;

2) итераций;

3) хорд;

4) касательных;

5) комбинированным методом хорд и касательных.

Составьте программы уточнения корня с точностью до = 0,5 • 10^-5 указанными методами, предусматривая вывод приближенного значения корня, числа итераций, обеспечивающих заданную точность, значение функции, расположенной в левой части уравнения в полученном приближении. Проанализируйте полученные результаты.

Вариант	Уравнение	Методы
16	x3+3x2-6=0	1,3

Для отделения корней уравнения, воспользуемся Excel и построим график функции.



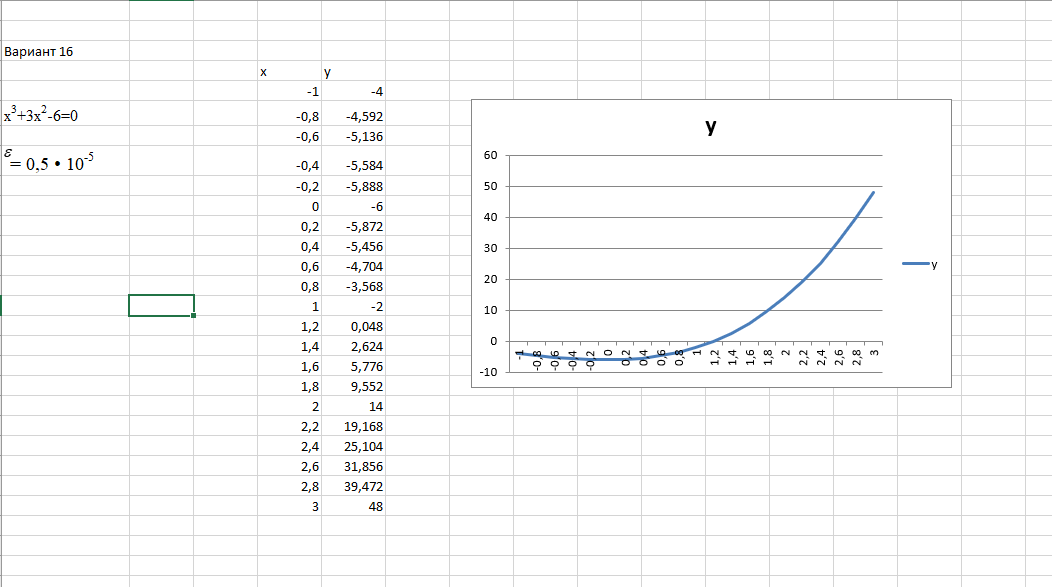
Рисунк 2.1 – График функции.
Можно заметить что уравнение имеет один корень[1;1.2].

Метод половинного деления:

Листинг 1.

program polovina;

uses crt;

var

a, b, e, x: real; i: integer;

function f(x: real): real;

begin

f := power(x,3)+3*power(x,2)-6;

end;

begin

clrscr;

i := 0;

---

writeln('введите a,b,e'); readln(a, b, e);

repeat

x := (a + b) / 2;

i := i + 1;

if f(x) * f(b) < 0 then a := x else b := x;

until abs(a - b) <= 2 * e;

writeln;

writeln('приближенное значение корня x0 = ', x:5:6);

writeln('значение функции в x0 = ', f(x):5:6);

writeln('кол-во итераций = ', i);

end.


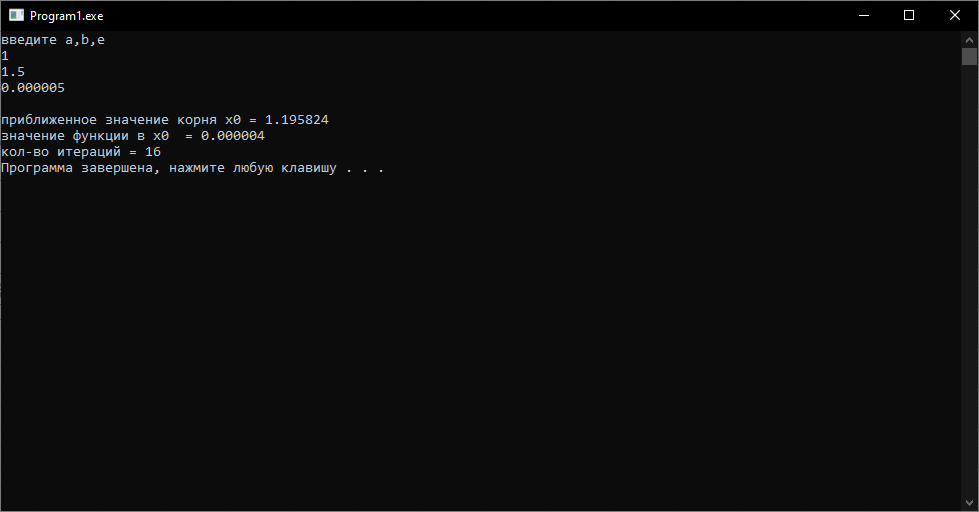
Рисунок 2.2 – Результат работы программы.

2. 
   Метод хорд.
   

Листинг программы:

program MetodHord;

uses Crt;

var

x, eps, a, b, c: real;

n: integer;

function f(x: real): real;

begin

f := power(x,3)+3*power(x,2)-6;

end;

begin

clrscr;

writeln('Введите a и b');

readln(a, b);

writeLn('Введите eps');

readln(eps);

clrscr;

n := 0;

repeat

c := (f(b) * a - f(a) * b) / (f(b) - f(a));

if f(a) * f(c) > 0 then a := c

else b := c;

Inc(n)

until abs((f(b) * a - f(a) * b) / (f(b) - f(a)) - c) < eps;

x := c;

writeLn('Корень x0 = ', x:5:6);

writeLn('Значение функции в x0 = ', f(x):5:6);

writeLn('Кол-во итераций = ', n);

readkey

end.



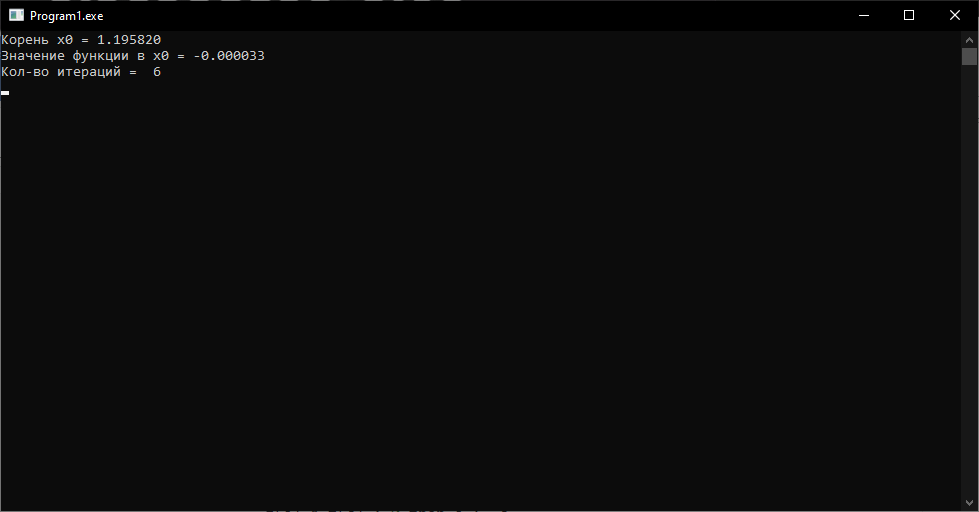
Рисунок 2.3 – Результат работы программы.

Задание 3. Интерполирование математических таблиц.

Дана таблица значений функции с верными цифрами:

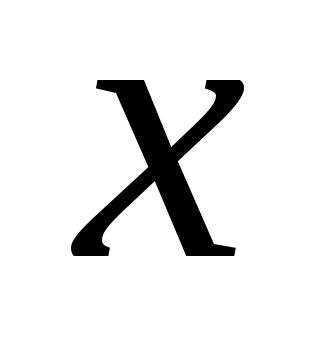
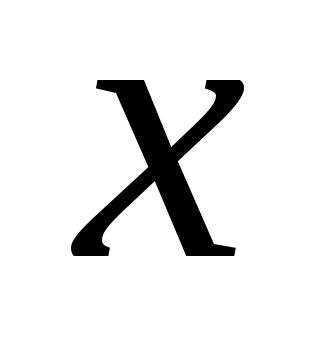
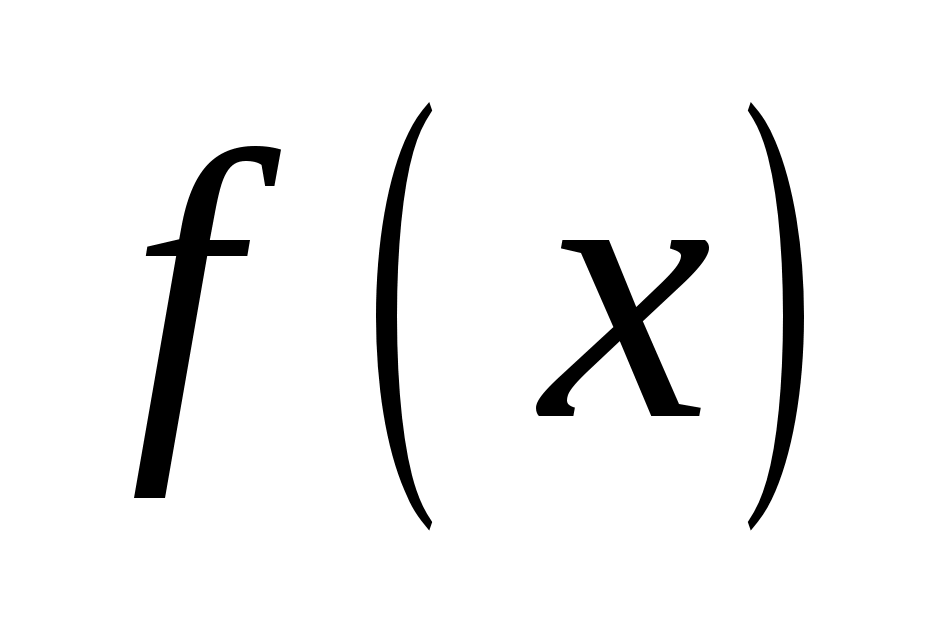
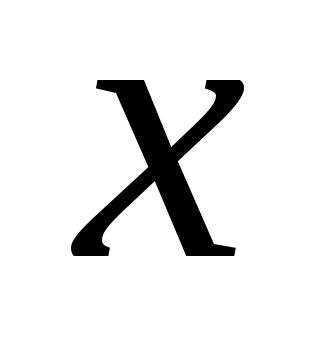
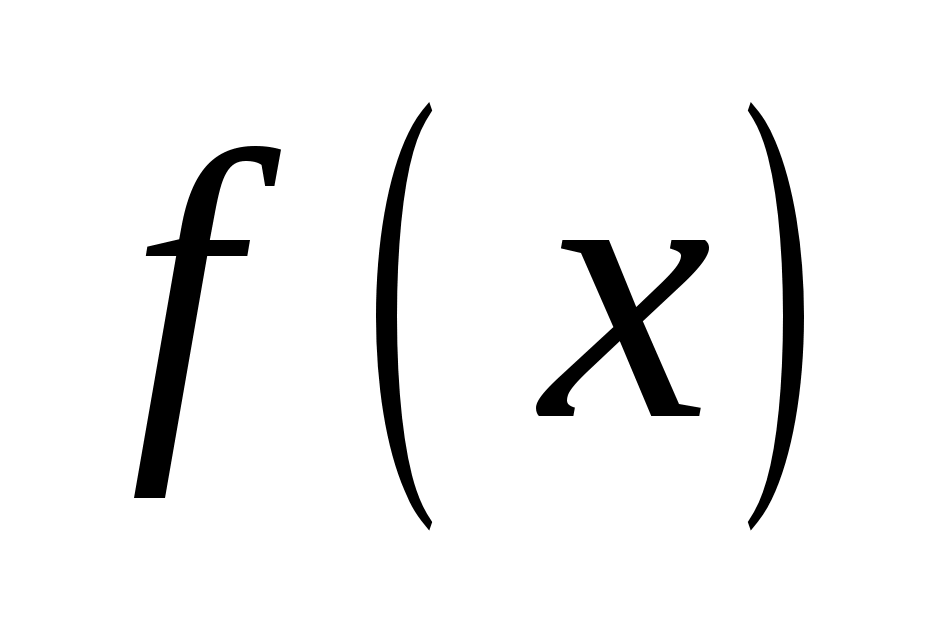
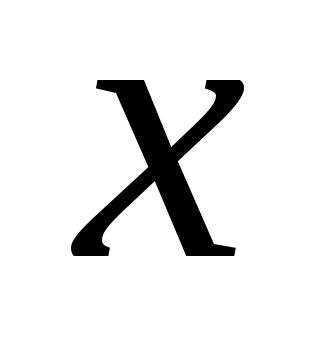
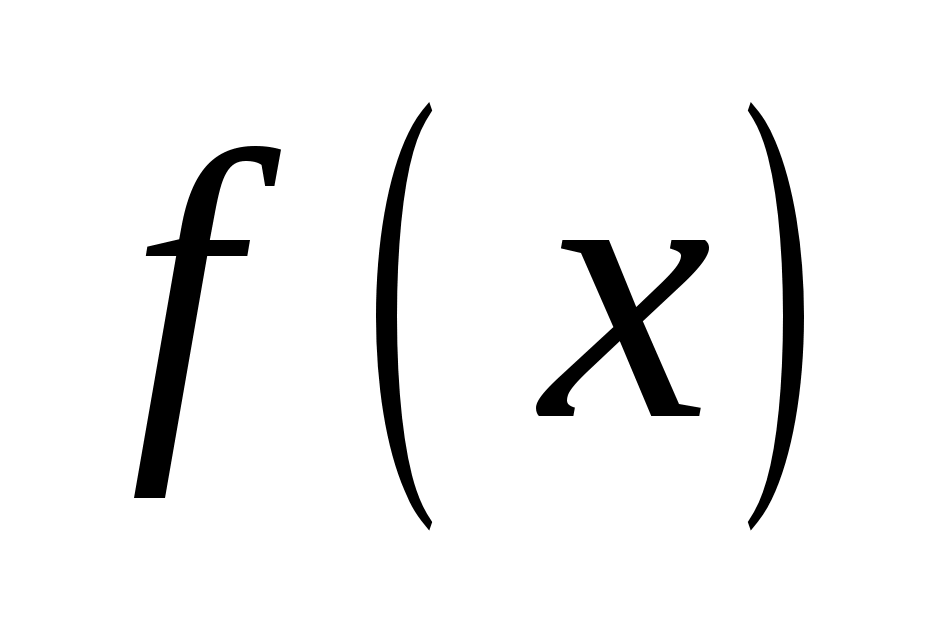
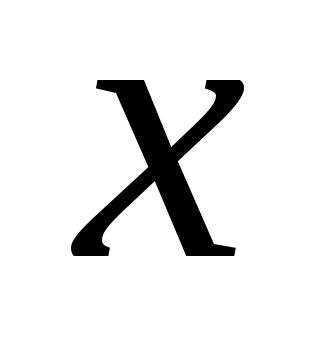
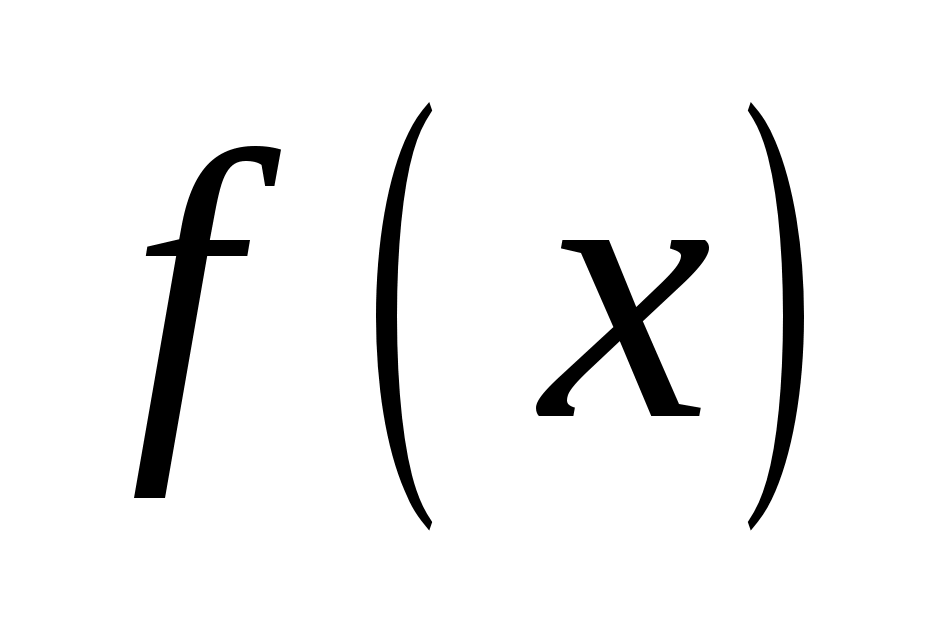
0	1	0,4	1,1024	0,8	1,5082	1,2	2,3881	1,6	3,9536
0,1	1,0053	0,5	1,1693	0,9	1,6763	1,3	2,7057	1,7	4,4823
0,2	1,0227	0,6	1,2575	1,0	1,8768	1,4	3,0696	1,8	5,0758
0,3	1,0543	0,7	1,3695	1,1	2,1130	1,5	3,4842	1,9	5,7396

---

1. 
   Составьте программу, для вычисления приближенного значения функции в точках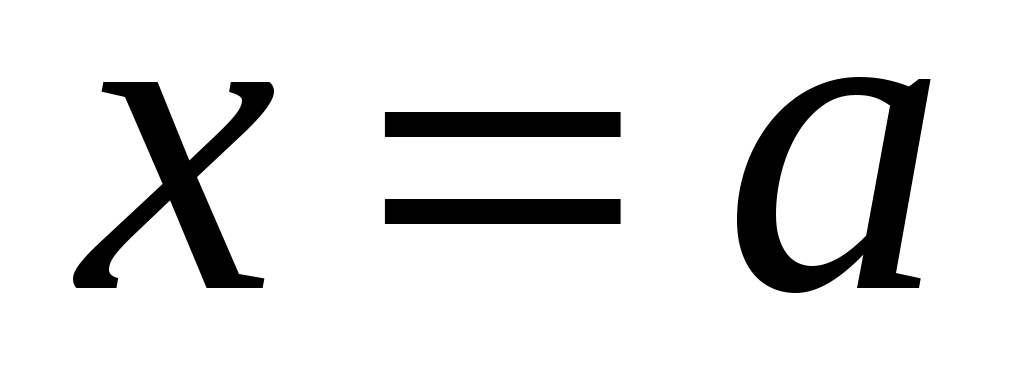 , 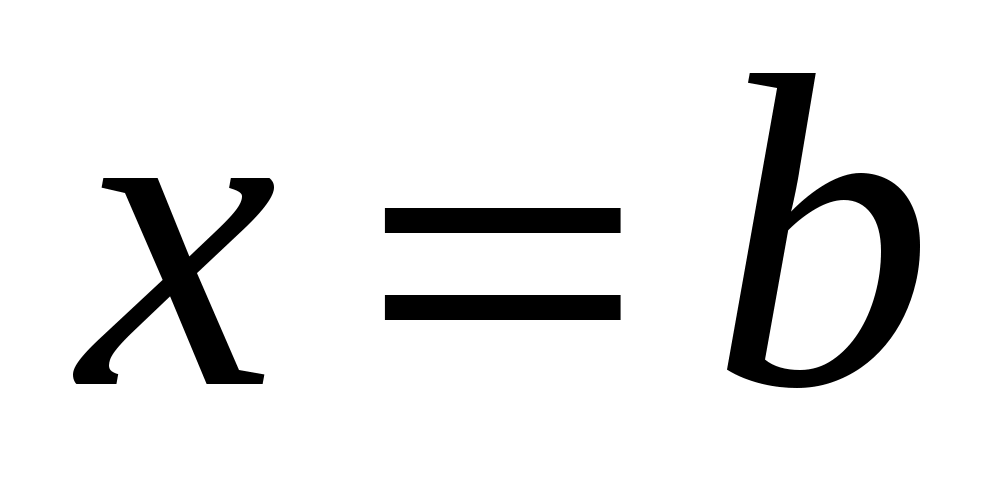с помощью интерполяционного многочлена Лагранжа 5 степени. (Для достижения наилучшей точности выберите узлы, расположенные симметрично относительно заданного значения ).
   
2. 
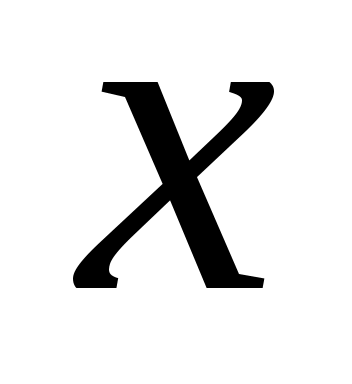   Сравните полученное значение со значением функции, вычисленным по ее аналитическому выражению, заданному в таблице.
   
3. 
   Определите абсолютную погрешность вычислений. Все исходные данные и числа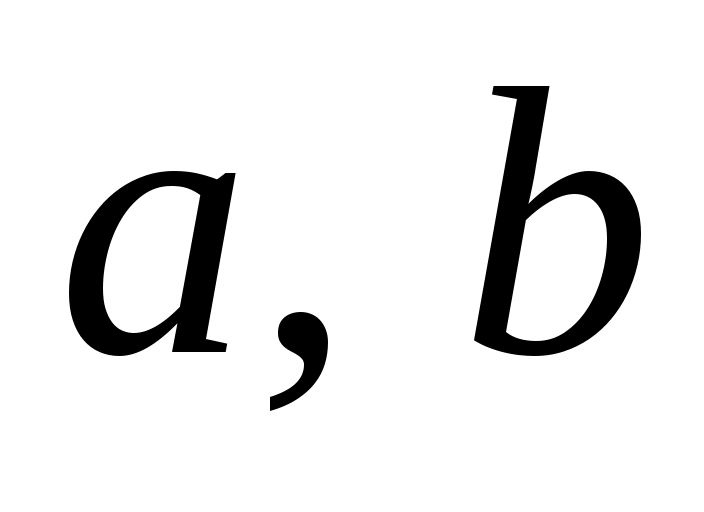 считаются точными числами.
   

Вариант 16 a= 0,25 b= 0,22
Листинг программы

Program 4;

const

N=20;

LnX=0. 0,25;

var

K,I:integer;

L,Ln:real;

X,Y:array [1..N] of real; begin

x[1]:=0; y[1]:=1.0;

x[2]:=0.1; y[2]:=1.0053;

x[3]:=0.2; y[3]:=1.0227;

x[4]:=0.3; y[4]:=1.0543;

x[5]:=0.4; y[5]:=1.1024;

x[6]:=0.5; y[6]:=1.1693;

x[7]:=0.6; y[7]:=1.2575;

x[8]:=0.7; y[8]:=1.3695;

x[9]:=0.8; y[9]:=1.5082;

x[10]:=0.9; y[10]:=1.6763;

x[11]:=1.0; y[11]:=1.8768;

x[12]:=1.1; y[12]:=2.1130;

x[13]:=1.2; y[13]:=2.3881;

x[14]:=1.3; y[14]:=2.7057;

x[15]:=1.4; y[15]:=3.0696;

x[16]:=1.5; y[16]:=3.4842;

x[17]:=1.6; y[17]:=3.9536;

x[18]:=1.7; y[18]:=4.4823;

x[19]:=1.8; y[19]:=5.0758;

x[20]:=1.9; y[20]:=5.7396;

L:=0;

for I:=1 to N do begin

Ln:=Y[i];

for K:=1 to N do

if I<>K then

Ln:=Ln*((Lnx-x[K])/(x[I]-x[K]));

L:=Ln+L;

end;

writeln('L=',L:1:10);

readln;

end.



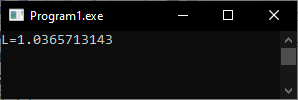
Рисунок 3.1 – Решение функции.


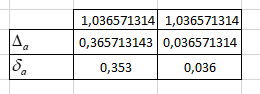
Рисунок 3.2 – Абсолютные погрешности.
Задание 4. Вычисление интегралов при помощи формул Ньютона-Котеса.

Вычислить определенный интеграл с заданной точностью указанными методами. Уточнять полученные значения используя метод Рунге-Ромберга. Предусмотреть вывод числа итераций, обеспечивающих заданную точность. Сравнить результаты.

Номер варианта	Интеграл	Точность	Методы
16			Средних прямоугольников Симпсона

---

Листинг программы:

double rez = 0,

h = 0.00001,

verh = 2,

nizh = 0.1,

tru = 0;

int k = 0;

for (double i = nizh; i < verh;)

{

tru = (Math.Sin(i) / Math.Sqrt(i));

rez = rez + tru;

tru = 0;

i = i + h;

k++;

}

Console.Write("Ответ: ");

Console.WriteLine(rez);

Console.Write("Кол-во итераций: ");

Console.WriteLine(k);

Console.ReadKey();



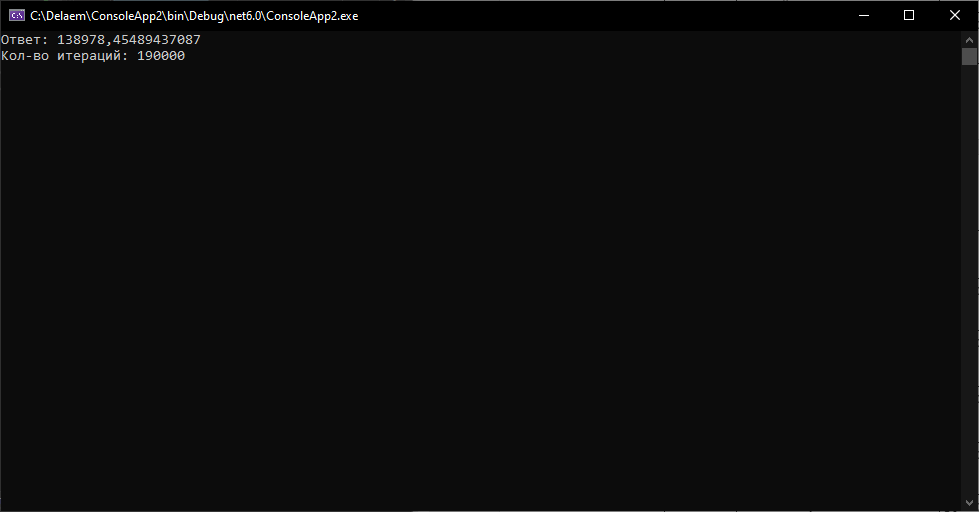
Рисунок 4.1 – Метод средних прямоугольников Симпсона.
Задание 5. Нахождение решений обыкновенных дифференциальных уравнений и систем дифференциальных уравнений при помощи формул Эйлера и Рунге – Кутта.

Составить программу для решения задачи Коши для заданного дифференциального уравнения на отрезке [0,1; 1,1] методами Эйлера и Рунге — Кутта 4 порядка с шагом h = 0,1 при начальном условии у(0, 1) = 0,25 с точностью 10^-5. Сравнить полученные результаты.

Номер варианта	A	B	C
16	0,166	1,3	0,461

Решение задачи Коши методом Эйлера.

Листинг программы:

program Eyler;

uses crt; var i,n:integer;

a,b,h,x,x0,y,y0,eps,emax,c:real;

function f(x,y:real):real;

begin

f:=a*(x*x+sin(b*x))+c*y;

end;

(*function ft(x:real):real;

begin

ft:=2/x;

end;*)

begin

clrscr;

writeln ('Решение задачи Коши методом Эйлера');

writeln ('Уравнение dy/dx=a*(x*x+sin(b*x))+c*y)');

write ('Введите интервал поиска решения [A,B]: ');

read (a,b);

write ('Введите число шагов N: ');

readln (n);

h:=(b-a)/n;

x0:=a;

write ('Введите начальное значение Y(0): ');

read(y0);

y:=y0;

x:=x0;

emax:=0;

writeln ('X':19,'Y':19);

for i:=1 to n+1 do begin

y:=y+h*f(x,y);

(*eps:=abs(y-ft(x));

if eps>emax then emax:=eps;

writeln (x:19:8,y:19:8);

x:=x+h;

end;

{writeln ('Pmax=',emax:19:8);}

readln;

end.



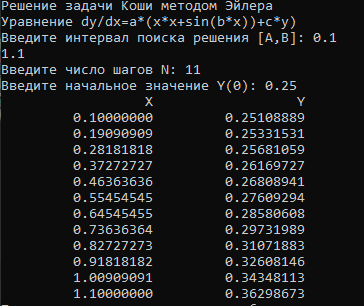
Рисунок 5.1 – Решение методом Эйлера.

Решение задачи Коши методом Рунге – Кутта.

Листинг программы:

program RungeKutta4;

function f(x, y: real): real;

begin

f := y + cos(x) - sin(x);

end;

function Yetalon(x: real): real;

begin

Yetalon := exp(x) + sin(x);

end;

procedure RungeKutta4Step(var t, y: real; h: real);

var

k1, k2, k3, k4: real;

begin

k1 := f(t, y);

k2 := f(t + (h / 2), y + k1 * (h / 2));

k3 := f(t + (h / 2), y + k2 * (h / 2));

k4 := f(t + h, y + k3 * h);

y := y + (k1 + 2 * k2 + 2 * k3 + k4) * h / 6;

t := t + h;

end;

procedure R(t0, tfin, h, y0: real; var yfin: real; Nprint: integer);

var

t: real;

y: real;

---