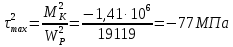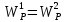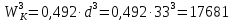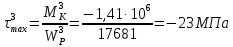Добавлен: 05.05.2024
Просмотров: 17
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Растяжение-сжатие
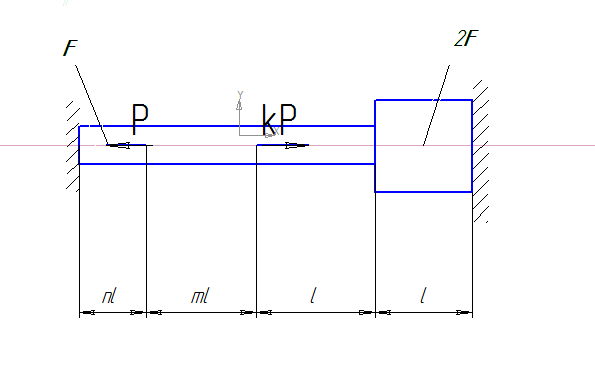
Исходные данные:
n=1;k=1;P =2 104 Н; F=500 мм2; l=400 мм; Е=2 105 МПа.
Заменим действие опор на стержень реакциями (
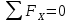 ;
;Ra+Kp-p+Rb=0;
Остальные уравнения статики дадут нам такое же выражение. В одно уравнение входят два неизвестных усилия (
Для расчета таких систем необходимо использовать уравнения, содержащие деформации элементов конструкций. Так как концы стержня жестко закреплены, то общая длина не изменяется:
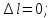
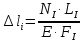 ;
;Выразим продольные усилия в поперечных сечениях стержня через одну из неизвестных реакций
Разделим стержень на участки по местам приложения сосредоточенных нагрузок и местам изменения поперечного сечения стержня. Для приведенной схемы получаем три участка
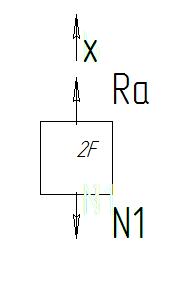
 ;
;Ra-N1=0;
N1=Ra.
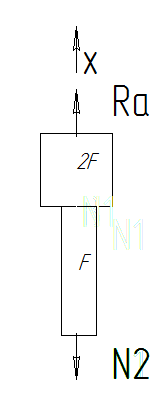
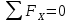 ;
;Ra-N2=0;
N2=Ra.
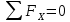 ;
;Ra+kP-N3=0;
N3=Ra + kP.
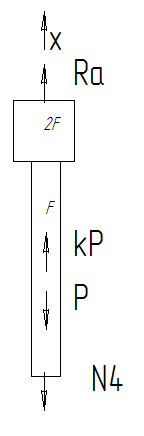
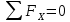 ;
;Ra+kP-P-N4=0;
N4=Ra + Kp - P.
Деформация участков
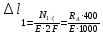
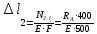
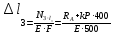
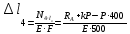
Общая деформация
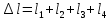 =
=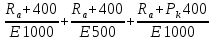 +
+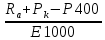 =0;
=0;2Ra+4Ra+4Ra+4Rk+4Ra+4P=0;
Отсюда Ra=-17 Кн.
Отрицательный знак указывает на то, что реакцию Ra нужно перенаправить в другую сторону.
Полуячаем Rb:
Rb=-Ra-kP+P=-3кН.
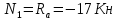
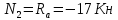
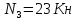
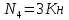
Построение эпюры нормальных напряжений:
Ϭ1=
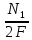 =
=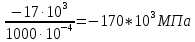 ;
; Ϭ2=
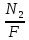 =
=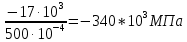 ;
;Ϭ3=
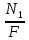 =
=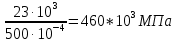 ;
;Ϭ1=
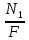 =
=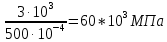 .
.На каждом участке определяем абсолютную продольную деформацию:
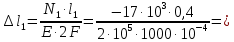 -0,34 мм;
-0,34 мм;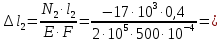 -0,68 мм;
-0,68 мм;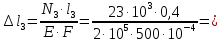 0,92мм;
0,92мм;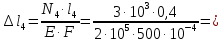 -0,23 10-3м = 0,12 мм;
-0,23 10-3м = 0,12 мм;Построение эпюры продольных перемещений u:
Определяем
продольные перемещения сечений, расположенных на границах участков:
uв=0; опорное сечение
uc=ub+
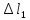 =0+0,12= 0,12 мм;
=0+0,12= 0,12 мм;uD=uс+
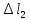 = 0,12+0,92= 1,04 мм;
= 0,12+0,92= 1,04 мм;uH=uD+
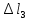 = 1,04-0,68= 0,36 мм;
= 1,04-0,68= 0,36 мм;uK=uH+
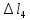 = 0,36-0,34= 0,02 мм;
= 0,36-0,34= 0,02 мм;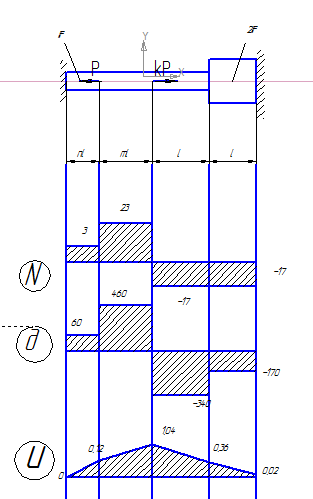
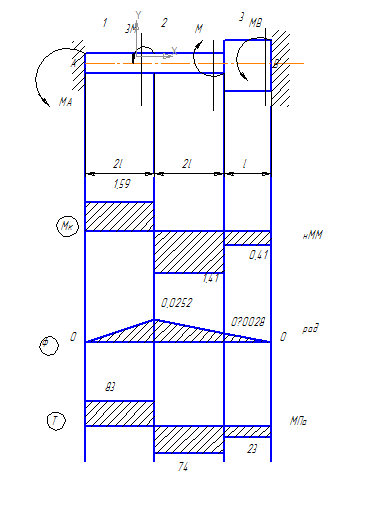
Кручение
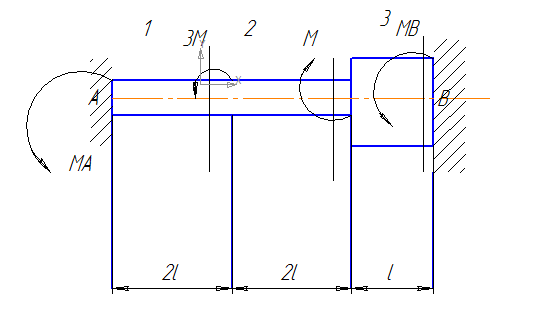
Исходные данные:
l=300м;G=8 104 МПа; М= 106 Нмм;
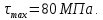
Составим уравнение
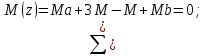
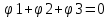
Учитывая, что
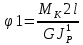
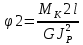
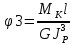
Получаем
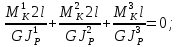
Сокращаем
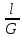 получаем
получаем
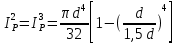 = 1,399.
= 1,399.При h\b=2
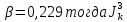 =phb3
=phb3h=2d b=d то
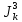 =0,458d4
=0,458d4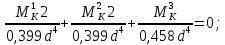
Сокращаем на d и получаем
С помощью метода сечений выражаем неизвестные крутящие моменты через один из реактивных опорных моментов.
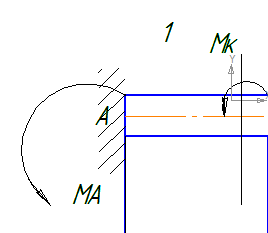
Mкz1 = −Ма
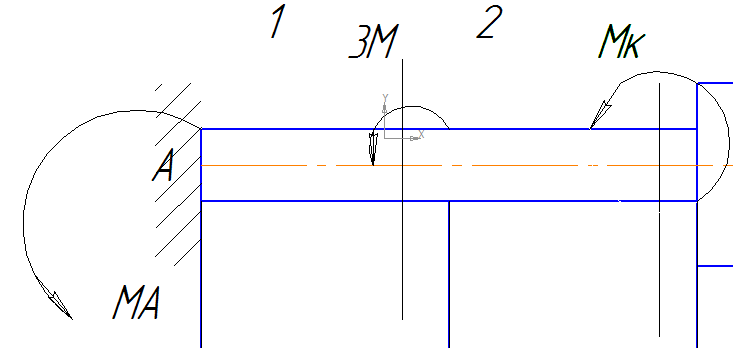
Mк2 = -Ма-3М
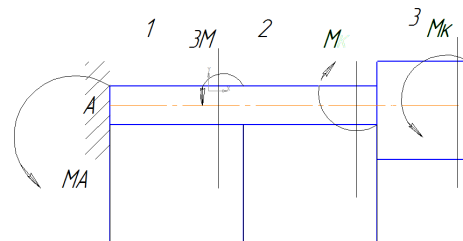
Mк3= -Ма-2М
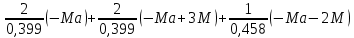 =0
=0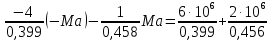
Отсюда
Ма = -1,59 106 Нмм
Теперь
Mкz1 = −Ма =1,59 106 Нмм
Mк2 = -Ма-3М = -1,41 106 Нмм
Mк3= -Ма-2М= -0,41 106 Нмм
Подбор размеров сечений производится по условиям прочности на первом участке
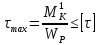
Для круглого сечения
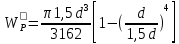 = 0,532d3.
= 0,532d3.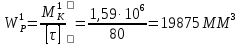
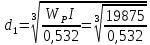 =33 ММ
=33 ММДля второго сечения
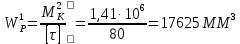
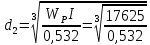 =32 ММ
=32 ММНа третьем сечении
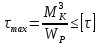
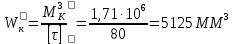
Для прямоугольного сечения
Wk=αhb2
При соотношении h/b=2 ( h=2d; b=d) тогда по таблице α=0,246
Wk=0,246 2d d2 = 0,492 d3
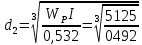 =22 ММ
=22 ММИз трех значений принимаем наибольшее
d=33 мм =0,033 м
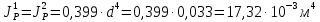
b=d=33 мм
h=2d= 66 мм
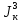 =0,299 0,0333 0,66 = 5,43 10-6 м4
=0,299 0,0333 0,66 = 5,43 10-6 м4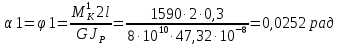
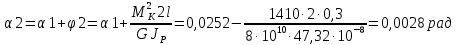
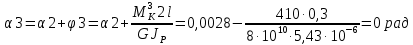
Максимальный угол закручивания
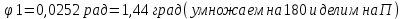
 =
=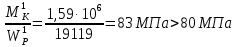
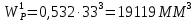
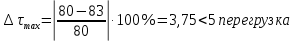 , допустимо
, допустимо