Файл: Курсовой проект по дисциплине Теплофизические процессы в электронных средствах.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.05.2024
Просмотров: 180
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
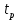 и
и 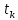 ; в месте крепления прибора к радиатору температура
; в месте крепления прибора к радиатору температура 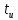 , а средняя температура основания радиатора
, а средняя температура основания радиатора 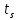 . При выборе радиатора предполагается, что удельная мощность рассеивания q задана и точка пересечения параметров
. При выборе радиатора предполагается, что удельная мощность рассеивания q задана и точка пересечения параметров 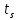 −
− 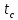 и q указывает область, которой соответствует определенный тип радиатора и условия охлаждения.
и q указывает область, которой соответствует определенный тип радиатора и условия охлаждения.Перегрев в месте крепления компонента к радиатору определяется по формуле:
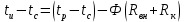 (5)
(5)где
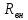 – внутреннее тепловое сопротивление прибора между рабочей областью и корпусом, обычно берется из ТУ, но если там оно не указано, то можно рассчитать по формуле;
– внутреннее тепловое сопротивление прибора между рабочей областью и корпусом, обычно берется из ТУ, но если там оно не указано, то можно рассчитать по формуле; 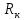 – тепловое сопротивление контакта, зависит от теплового сопротивления термопасты или силиконовой прокладки;
– тепловое сопротивление контакта, зависит от теплового сопротивления термопасты или силиконовой прокладки; 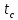 – температура окружающей среды, берется из ТЗ;
– температура окружающей среды, берется из ТЗ; 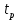 – предельная температура рабочей области прибора, берется из ТУ;
– предельная температура рабочей области прибора, берется из ТУ; 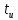 – температура в месте крепления прибора к радиатору, Ф – мощность, которую должен рассеять радиатор, равна мощности транзистора.
– температура в месте крепления прибора к радиатору, Ф – мощность, которую должен рассеять радиатор, равна мощности транзистора. 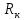 − данное сопротивление практически полностью обусловлено качеством присоединения модуля к охладителю. Разумеется, при присоединении модуля все винты должны быть затянуты (и затянуты в правильном порядке), неплоскостность охладителя должна быть минимальна (в идеале - не более 30 мкм), шероховатость так же должна быть минимальна (не более 2,5 мкм). Но даже в таких идеальных условиях величина ????к не совсем понятна, необходим расчёт (6).
− данное сопротивление практически полностью обусловлено качеством присоединения модуля к охладителю. Разумеется, при присоединении модуля все винты должны быть затянуты (и затянуты в правильном порядке), неплоскостность охладителя должна быть минимальна (в идеале - не более 30 мкм), шероховатость так же должна быть минимальна (не более 2,5 мкм). Но даже в таких идеальных условиях величина ????к не совсем понятна, необходим расчёт (6).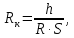
(6)
где h – толщина прокладки; R – тепловое сопротивление материала прокладки/термопасты (термическое сопротивление корпус-радиатор); S – площадь прокладки/термопасты.
Толщина слоя пасты, в идеальном случае, должна составлять 0,02…0,05 мм, но допустим слой и до 0,1 мм. На практике, толщина слоя обычно составляет около 0,1 мм, а порою доходит и до 0,2…0,3 мм при значительной шероховатости или неплоскостности охладителя.
Представим реальный случай: контакт радиатора с транзистором осуществляется термопастой ZALMAN ZM – STG2 с
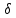 = 30 мкм, ???? = 4,1 Вт/(м ∙ К) и без силиконовой прокладки.
= 30 мкм, ???? = 4,1 Вт/(м ∙ К) и без силиконовой прокладки.Площадь контакта корпуса транзистора с радиатором, исходя из рисунка нашего транзистора с его параметрами, будет равна:
S = 6,8
 5,5= 37,4
5,5= 37,4 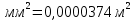 .
.Тогда
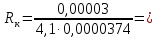 0,19 К/Вт
0,19 К/ВтМаксимальная температура p-n перехода рассчитывается по формуле (7).
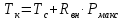 , (7)
, (7)Из ТУ:
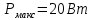 ,
, 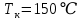 ,
, 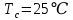 .
.Мы видим, что мощность транзистора P не превышает
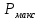 , следовательно данный транзистор можно применять в этих условиях.
, следовательно данный транзистор можно применять в этих условиях.Из формулы (6) следует, что
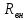 можно найти по формуле (8).
можно найти по формуле (8).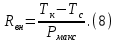
Тогда
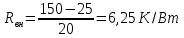 .
.Вернемся к формуле (5) , подставим значения и получим перегрев в месте крепления компонента к радиатору:
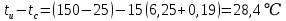
Необходимо определить средний перегрев основания радиатора.
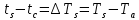 , (9)
, (9)где
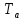 температура окружающей среды, а
температура окружающей среды, а 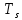 температура радиатора.
температура радиатора.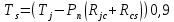 , (10)
, (10)где
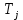
– температура кристалла (120
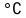 ),
), 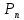 – мощность потерь прибора (15Вт),
– мощность потерь прибора (15Вт), 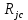 – тепловое сопротивление кристалл-корпус (2,5К/Вт),
– тепловое сопротивление кристалл-корпус (2,5К/Вт), 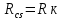 – тепловое сопротивление корпус-радиатор (0,19К/Вт).
– тепловое сопротивление корпус-радиатор (0,19К/Вт). 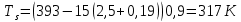
Подставим имеющиеся значения в формулу (9) и получим перегрев основания радиатора:
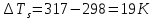
Теперь, для выбора радиатора остается только рассчитать удельную плотность теплового потока, рассеиваемого радиатором (11).
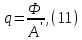
Ф – тепловой поток, рассеиваемый радиатором, который равен мощности транзистора (Ф = 15 Вт); F– площадь основания радиатора. Для расчета радиатора можно использовать следующие данные: для рассеивания 1 Вт тепла, достаточно использовать площадь теплоотвода, равную
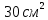 .
.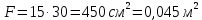 .
.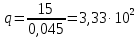 .
.Суммарное сопротивление на участке кристалл - окружающая среда можно определить по следующей формуле:
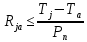 , (12)
, (12)где
 - температура окружающей среды (25
- температура окружающей среды (25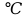 ).
).Подставляем данные и получаем, что суммарное сопротивление на участке кристалл-окружающая среда равно:
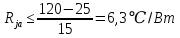 ,
,На рисунке 6 представлена эквивалентная схема теплопередачи от кристалла в окружающую среду.
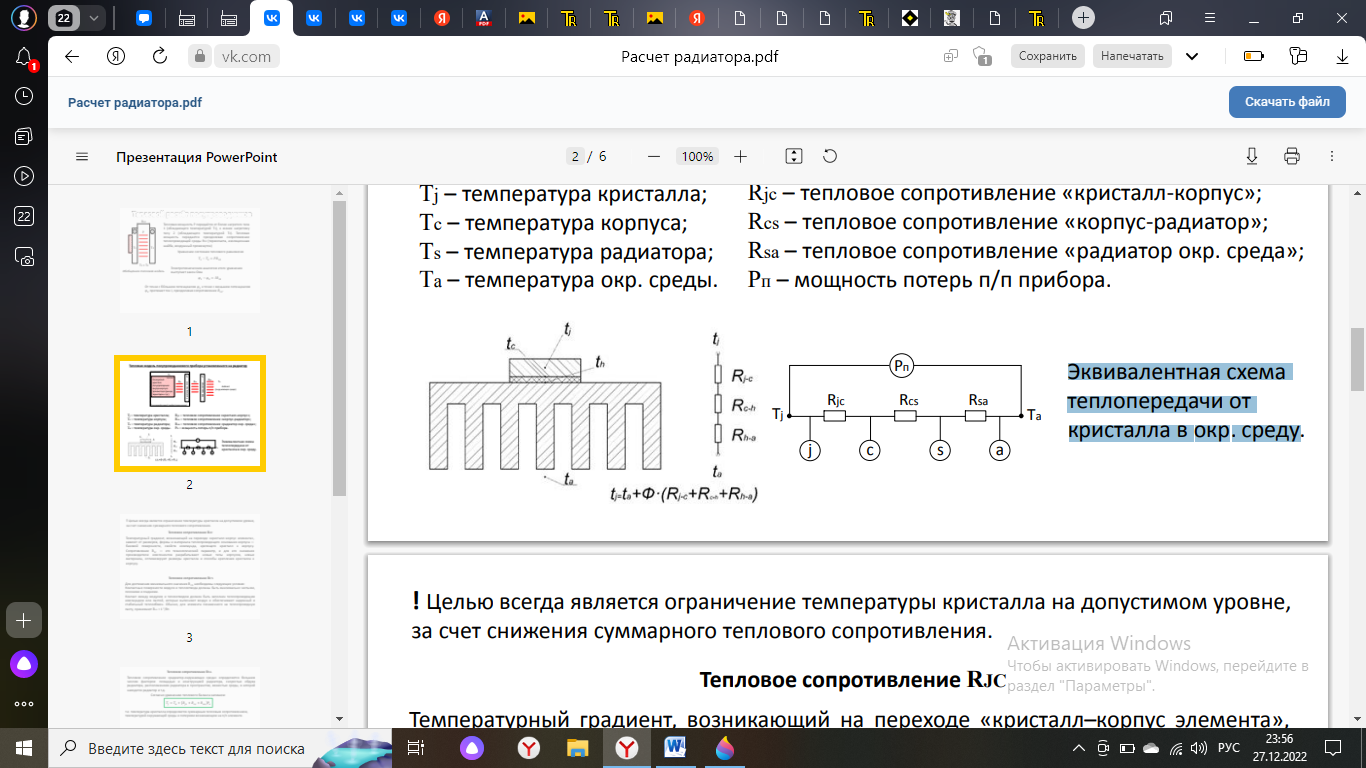
Рисунок 5 – Эквивалентная схема теплопередачи.
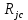 – Сопротивление кристалл - корпус ;
– Сопротивление кристалл - корпус ; 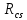 – Сопротивление корпус – радиатор;
– Сопротивление корпус – радиатор; 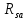 – Сопротивление радиатор – окружающая среда;
– Сопротивление радиатор – окружающая среда;
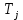 - Температура кристалла ;
- Температура кристалла ; 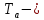 Температура окружающей среды; Рп – Мощность потерь прибора.
Температура окружающей среды; Рп – Мощность потерь прибора.Тепловое сопротивление радиатора рассчитывается по формуле:
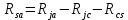 (13)
(13)Подставляем имеющиеся у нас значения и получаем, что тепловое сопротивление радиатора равно:
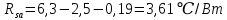
Сделаем проверку с помощью онлайн расчета радиатора:
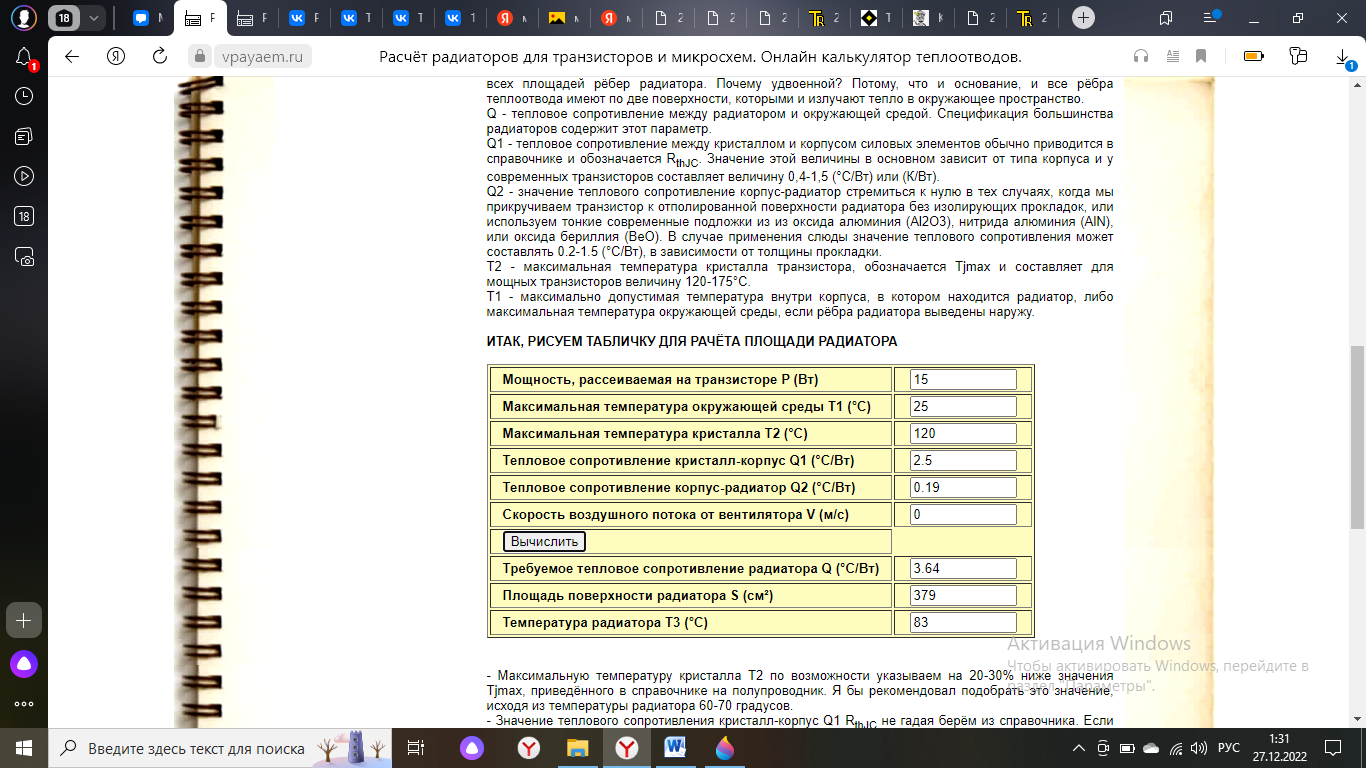
Рисунок 6 – Таблица расчета радиатора для транзистора 2SA1244.
Наши данные сходятся с данными из онлайн расчета с небольшими погрешностями, из чего можно сделать вывод, что расчет проведет верно.
Тип радиатора будем выбирать по графикам на рисунке 6.
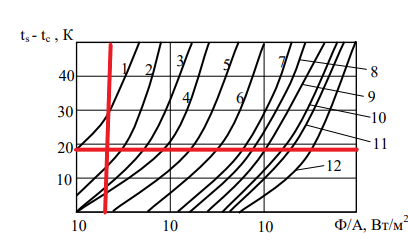
Рисунок 7 – Графики выбора типа радиатора: при свободной конвекции – пластичные (1), ребристые (1…4), игольчато-штыревые (1…5), при вынужденной конвекции – пластичные (3), ребристые (6…8), петельнопроволочные (8,9), жалюзные (10,11), игольчато-штыревые (11,12)
По графику на рисунке 7 видно, что для охлаждения радиатора 2SA1244 можно использовать ребристый радиатор.
Для дальнейшего расчета нужно определить коэффициент теплоотдачи
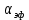 – характеризующий интенсивность теплообмена между поверхностью тела и окружающей средой по формуле (11).Коэффициент
– характеризующий интенсивность теплообмена между поверхностью тела и окружающей средой по формуле (11).Коэффициент 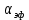 показывает какое количество тепла передается от единицы поверхности стенки к жидкости в единицу времени при разности температур между стенкой и жидкостью в 1 градус (К).
показывает какое количество тепла передается от единицы поверхности стенки к жидкости в единицу времени при разности температур между стенкой и жидкостью в 1 градус (К).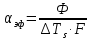 . (14)
. (14)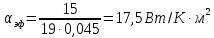 .
.Теперь по рисунку 7, на котором изображены кривые коэффициента теплоотдачи радиаторов при свободном воздушном охлаждении, и по таблице 1 выберем некоторые размеры радиатора.
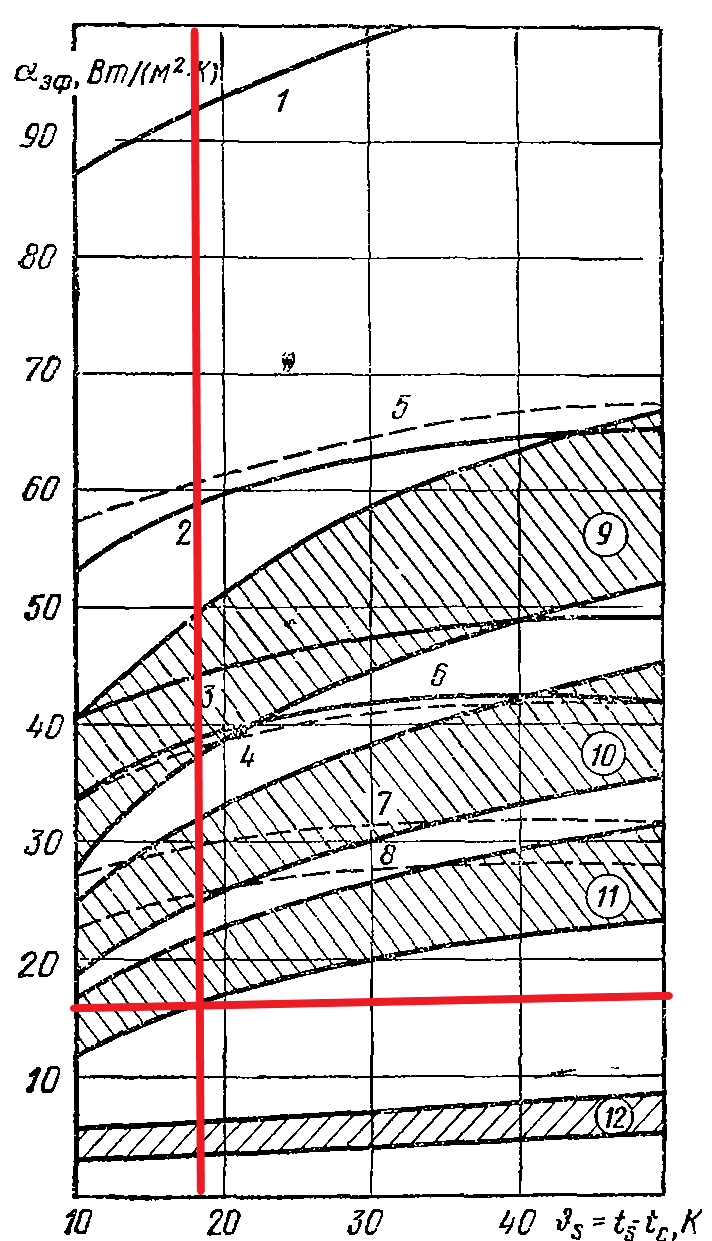
Рисунок 8 – Эффективный коэффициент теплоотдачи радиаторов при свободном воздушном охлаждении.
На рисунке 8 приведены графики для игольчато штыревых радиаторов с различным шагом (сплошные кривые 1,2,3,4 и пунктирные кривые 5,6,7,8). Заштрихованные области 9, 10, 11 относятся к ребристым радиаторам. Рассчитанные данные попадают в область 9. Теперь будем использовать таблицу 1 для нахождения размеров радиатора.
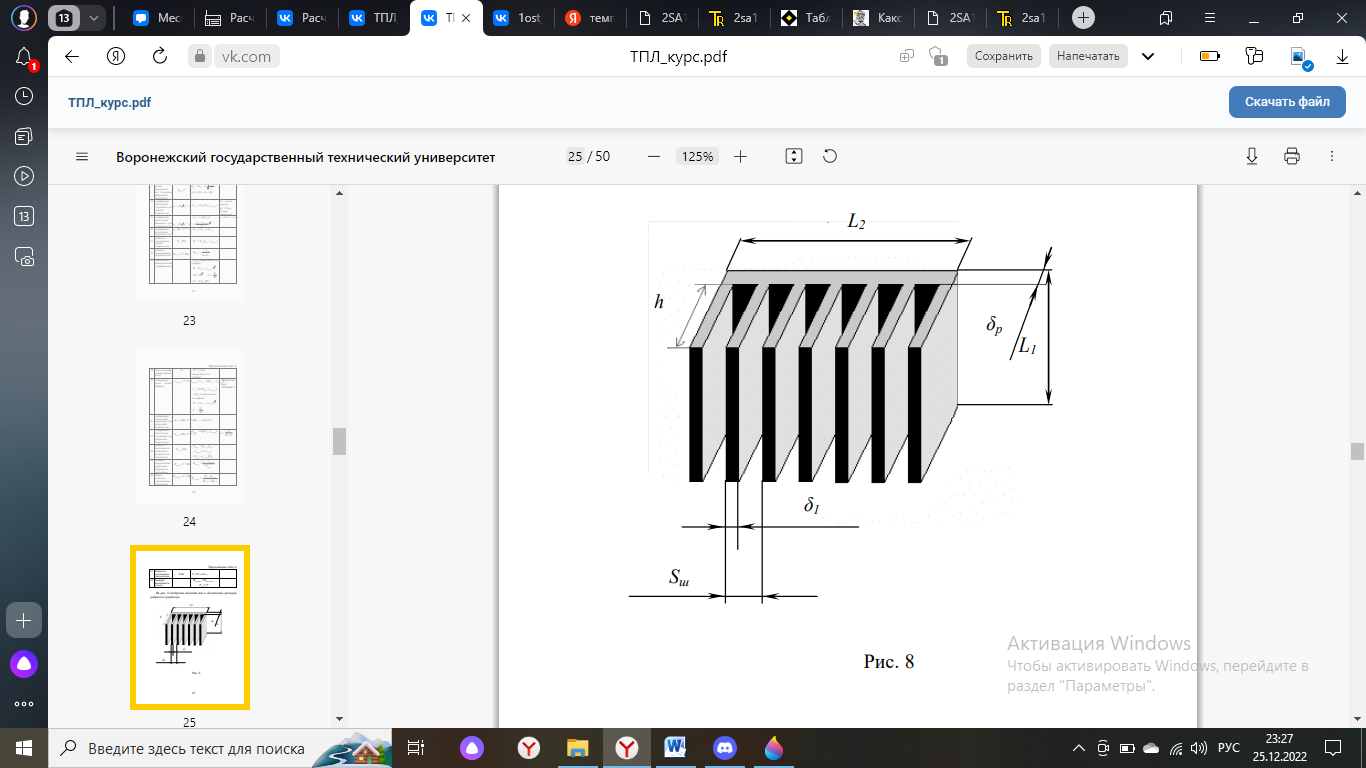
Рисунок 9 – Пример ребристого радиатора с обозначениями
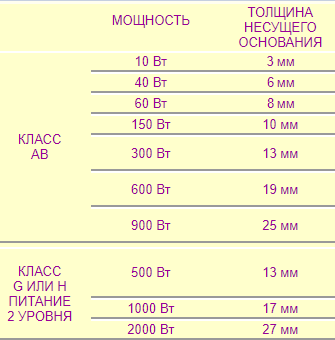
Рисунок 10 - Зависимость толщины теплоотвода от мощности.
На рисунке 10 можно увидеть толщины теплоотвода от мощности, исходя из этой зависимости, мы можем определить, что для нашей мощности подходит толщина плиты в пределах от 3 до 6 мм. Толщину моего радиатора я возьму 4 мм.
Зададим параметры радиатора:
- Толщина ребра d = 0,001 м;
- Толщина плиты теплоотвода
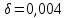 м;
м;- Расстояние между ребрами b = 0,01 м
- Высота ребра h = 0,02 м;
- Протяженность ребра L = 0,07 м
Рассчитаем число ребер n по формуле (15).
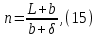
Тогда:
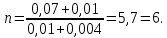
Длину плиты теплоотвода, на которой развиты ребра, можно найти по формуле (16).
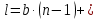 δ ∙
δ ∙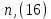
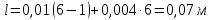
Площадь гладкой поверхности теплоотвода можно найти по формуле (17).
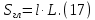
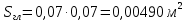 .
.Площадь ребристой поверхности для одностороннего теплоотвода при креплении полупроводникового прибора с гладкой стороны,
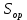 определяется по следующей формуле:
определяется по следующей формуле: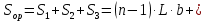 (δ+2∙h )
(δ+2∙h )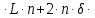 h
h (18)
(18)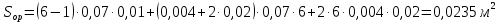
Тепловое сопротивление радиатора
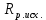 рассчитывается по формуле (19).
рассчитывается по формуле (19).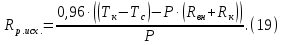
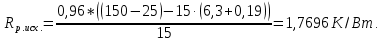
Средняя поверхностная температура радиатора
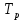 вычисляется по формуле (20).
вычисляется по формуле (20).
