Добавлен: 06.05.2024
Просмотров: 61
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
= (d+(1), d+(2), …, d+(n))
dA = (d-(1), d-(2), …, d-(n))
Поэтому верно следующее утверждение, являющееся аналогом леммы о рукопожатиях.
Утверждение 4. Сумма полустепеней исхода всех вершин орграфа равна сумме полустепеней захода и равна числу его дуг:

Нетрудно убедиться в том, что равенство (2) не является достаточным условием для существования бинарной n*m – матрицы А с векторами строчных сумм сA и столбцовых сумм dA. Например, нет матрицы А, для которой сA = (3, 0), dA = (2, 1).
Пара векторов c = (c1, c2, …, cm), d = (d1, d2, …, dn) с целыми неотрицательными координатами называется графической, если существует бинарная m*n – матрица А, для которой сА = с, dА = d. Если истолковывать эту матрицу как приведенную матрицу смежности двудольного графа, то вектор сА окажется списком степеней вершин этого графа, принадлежащих одной доле, а вектор dА — списком степеней вершин другой доли, так что условия графичности пары векторов являются условиями существования соответствующего двудольного графа — реализации этой пары. Этим и объясняется термин «графическая пара векторов».
При m = n ту же матрицу А можно истолковывать как матрицу смежности орграфа, и тогда условия графичности пары векторов станут условиями существования ориентированного графа с заданными списками полустепеней исхода и полустепеней захода вершин.
Критерий графичности пары векторов устанавливается следующей теоремой.
Теорема 5. Пара векторов
c = (c1, c2, …, cm), d = (d1, d2, …, dn) (3)
является графической тогда и только тогда, когда выполняются следующие два условия:
1) последовательность
(c1+m-1, c2+m-1, …, cm+m-1, d1, d2, …, dn) (4)
графическая;
2)
Очевидно, что пара векторов (3) реализуется двудольным графом тогда и только тогда, когда последовательность (4) реализуется расщепляемым графом, для которого (c
1+m-1, c2+m-1, …, cm+m-1) и (d1, d2, …, dn) — списки степеней вершин верхней и нижней долей соответственно. Поэтому доказываемое непосредственно вытекает из критерия расщепляемости графической последовательности.
Коснемся вопроса о реконструируемости орграфов. Гипотезу Келли — Улама для ориентированных графов можно попытаться сформулировать так же, как и для неориентированных. Но для орграфов эта гипотеза не верна.
П. Стокмейер (1977, 1981 гг.) нашел несколько семейств нереконструируемых орграфов. Одно из них состоит из сильных турниров специального вида. Два нереконструируемых турнира изображены на рис. 4. Ф. Харари и Е. Палмер доказали (1967 г.), что любой турнир, не являющийся сильным, реконструируем.
Рис. 4.
А. Рамачандран предложил новый вариант гипотезы реконструируемости для орграфов. Пусть G — ориентированный граф. Вместе с каждым подграфом Gv = G — v, v VG, будем рассматривать упорядоченную пару (d+(v), d-(v)) полустепеней исхода и захода вершины v. Орграф G назовем N-реконструируемым, если он определяется с точностью до изоморфизма набором {(Gv, d+(v), d-(v)): v VG}.
Гипотеза Рамачандрана (1981 г.). Любой орграф N-реконструируем.
Эта гипотеза пока не доказана и не опровергнута.
Пусть
М = (P1, P2,…, Pi) (5)
— какое-либо множество путей орграфа G, попарно не имеющих общих вершин. Если множества VPi вершин этих путей составляют разбиение для VG, т. е.
VG = VP1 VP2 ... VPi,
то множество путей М называется разбиением орграфа G на пути. Минимальное число l путей, составляющих разбиение орграфа G, обозначим через l(G).
Ниже фигурируют понятия числа независимости 0(G) и хроматического числа (G) орграфа G, которые для ориентированных графов определяются так же, как и для неориентированных, т. е. 0(G) = 0(Gb), (G) = (Gb).
Теорема 6. Для любого орграфа G верно неравенство l(G) 0(G)
Фиксируем некоторое разбиение (2) орграфа G на пути. Пусть N(M) = (a1, a2, …, ai), ai Рi — множество начальных вершин этих путей. Докажем более сильное утверждение:
существует такое разбиение М' орграфа G на пути, что
N(M’) N(M), |M’| 0(G)
Доказательство последнего утверждения проведем индукцией по n = |G|. Утверждение очевидно при n = 1, 2. Пусть n > 2 и утверждение верно для орграфов, порядки которых меньше n.
Вначале покажем, что, не ограничивая общности, можно считать |М|
0(G)+1. В самом деле, пусть |М| 0(G)+2. Рассмотрим орграф G1 = G —VP1. Очевидно, что 0(G1) . 0(G). По индуктивному предположению существует разбиение М1 орграфа G1 на пути с N(M1) N(M) и |М1| 0(G1) 0(G). Но тогда М' = M1 P1 — разбиение орграфа G с N(M')N(M) и |М’| 0(G)+1. Поэтому всегда можно считать, что |М| 0(G)+1.
Пусть теперь |М| = 0(G)+1. Тогда множество N(M) = (a1, a2, …, ai) не является независимым, т. е. в нем есть хотя бы одна пара смежных вершин. Предположим, что (a1, a2) AG. Если путь P1 состоит из единственной вершины a1, то объединив P1 и P2 в путь (a1, a2, …), получим нужное разбиение.
Если же путь Р = (а1, b1, ...) имеет более чем одну вершину, то рассмотрим орграф G1 = G—a1. По индуктивному предположению существует такое разбиение M1 орграфа G1 на пути, что |М1| 0(G1) 0(G) и N(M1) = {b1, a2, a3, ..., аi}. Если b1 N(M1), то М' получим из M1, добавив вершину a1 к пути, начинающемуся в b1. Аналогично можно поступить и тогда, когда а2 N(M1). Если же b1 N(M1) и a2 N(M1), то М' = M1 {(a1)}.
Из теоремы 6 вытекают два важных следствия.
Орграф G называется транзитивным, если истинна импликация
((x, y) AG и (y, z) AG) (x, z) AG
Следствие 7. Если орграф G транзитивен, то l(G) = 0(G).
Согласно предыдущей теореме l(G) 0(G). Но две вершины транзитивного орграфа, принадлежащие одной цепи, смежны, поэтому 0(G)l(G). Итак, l(G) = 0(G).
Следствие 8. В каждом турнире существует гамилътонов путь.
Поскольку любые две вершины, произвольного турнира Т смежны, то 0(T)=1. Поэтому существует цепь Р, содержащая все вершины турнира Т.
Для сильных турниров верно следующее более общее утверждение.
Теорема 9. Пусть Т — сильный турнир порядка n. Тогда для любой его вершины u и для любого числа k, 3 k n, в Т есть контур длины k, содержащий вершину u.
Пусть S (u) и Р(u) — множество всех тех вершин v и, соответственно, w турнира Т, для которых (u, v) AT и (w, u) АТ. Оба эти множества не являются пустыми, поскольку орграф Т сильный. По той же причине существует хотя бы одна дуга (v, w), идущая из S (u) в Р(u) (рис. 5). Следовательно, вершина и лежит на контуре длины 3.
Далее воспользуемся индукцией по k. Пусть вершина u входит в контуры всех длин от 3 до k, где k < n. Покажем, что она входит в контур длины k + 1.
Пусть С=(v0, v1, …, vk), v0 = vk = u, — контур длины k. Предположим, что для некоторой вершины w, не входящей в этот контур, существуют такие дуги (w, x) и (у, w), что x VC и у VC. Тогда в С есть такие две смежные вершины vi, и vi+1, что (vi, w) и (w, vi+1)—дуги турнира Т.
Следовательно, вершина u входит в контур
С=(v0, v1, …, vi, w, vi+1, …, vk)
v0 = vk = u
длины k + 1.
Рис. 5.
Если же указанной выше вершины w нет, то множество вершин турнира Т, не входящих в контур С, можно разбить на две части S (С) и Р(С) так, чтобы для любых вершин aS(C), bP(C) и v С выполнялись условия (v, а) AG и (b, v) AG. Так как орграф T сильный, то S(С) и Р(С) не пусты и существует дуга, идущая из некоторой вершины a S(С) в некоторую вершину b Р(С) (рис. 6). Таким образом, вершина u входит в контур
С‘ = (v0, a, b, v2, …, vk)
длины k + 1.
Очевидно
Следствие 10. Сильный турнир гамильтонов. Заметим, что предыдущее следствие вытекает также из теоремы 9.
Теорема 11. Если k—максимальная длина путей в орграфе G, то (G).k + 1.
Обозначим через В такое минимальное относительно включения подмножество в АG, что орграф G1 = G — В не имеет контуров. Для любой вершины v определим t(v) как число вершин пути в орграфе G1 с началом в v, имеющем максимальную длину. Приписав каждой вершине v цвет t(v), получим раскраску орграфа G не более чем k + 1 цветами. Остается доказать, что эта раскраска правильная, т. е. что t(u) t(v) для любых двух смежных вершин u и v. Но если (u, v) АG1, то t(u)>t{v). Если же (u, v) В, то G1+(u,v) имеет контур. Поэтому в G1 существует (v, u) - путь и, следовательно, t(v)>t(u).
Итак, доказано, (G).k + 1.
Рис. 6.
Матрицей достижимости графа с n вершинами называется квадратная матрица R порядка n, элементы которой определяются следующим образом:

Матрицей контрдостижимости графа с n вершинами называется квадратная матрица Q порядка n, элементы которой определяются следующим образом:


Матрицей сильной связности орграфа с n вершинами называется квадратная матрица S порядка n, элементы которой определяются следующим образом:

При машинной реализации алгоритмов на графах матрицы расстояний, достижимости, контрдостижимости и сильной связности можно определять через матрицу смежности.
Пусть дан граф G, - его матрица смежности. Элементы матрицы расстояний D можно вычислить при машинной реализации следующим образом: dij равно наименьшему из чисел n, для которых aijn > 0, где aijn - элемент матрицы An и равно бесконечности, если таких чисел нет.
- его матрица смежности. Элементы матрицы расстояний D можно вычислить при машинной реализации следующим образом: dij равно наименьшему из чисел n, для которых aijn > 0, где aijn - элемент матрицы An и равно бесконечности, если таких чисел нет.
Пример. Дан граф G (рис. 7). Найти матрицу расстояний D.
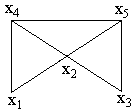
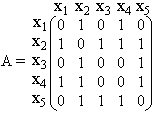
Рис. 7
Сначала найдем матрицу смежности A, элемент aij которой равен 1, если вершины xi и xj графа G смежны, и равен нулю в противном случае. В матрице D диагональные элементы будут равны нулю, так как расстояние между вершинами xi и xj, если i = j, считается равным нулю. Если элемент aij матрицы A равен 1, то соответствующий элемент dij матрицы D тоже будет равен 1. Недоопределенная матрица D изображена ниже.
Умножим матрицу А саму на себя по правилу умножения матриц и найдем матрицу A2.
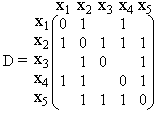
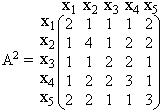
Так как в матрице A2 нет нулевых элементов, то оставшиеся неопределёнными элементы матрицы D равны 2. Окончательно матрица D будет иметь вид:
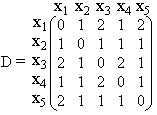
Матрицу достижимости R можно найти с помощью матрицы смежности А следующим образом R = T(E+A+A2+...+An-1), где n число вершин, E единичная матрица, а оператор T определяется следующим образом:

Матрица контрдостижимости Q находится транспонированием матрицы достижимости R: Q = R
dA = (d-(1), d-(2), …, d-(n))
Поэтому верно следующее утверждение, являющееся аналогом леммы о рукопожатиях.
Утверждение 4. Сумма полустепеней исхода всех вершин орграфа равна сумме полустепеней захода и равна числу его дуг:
Нетрудно убедиться в том, что равенство (2) не является достаточным условием для существования бинарной n*m – матрицы А с векторами строчных сумм сA и столбцовых сумм dA. Например, нет матрицы А, для которой сA = (3, 0), dA = (2, 1).
Пара векторов c = (c1, c2, …, cm), d = (d1, d2, …, dn) с целыми неотрицательными координатами называется графической, если существует бинарная m*n – матрица А, для которой сА = с, dА = d. Если истолковывать эту матрицу как приведенную матрицу смежности двудольного графа, то вектор сА окажется списком степеней вершин этого графа, принадлежащих одной доле, а вектор dА — списком степеней вершин другой доли, так что условия графичности пары векторов являются условиями существования соответствующего двудольного графа — реализации этой пары. Этим и объясняется термин «графическая пара векторов».
При m = n ту же матрицу А можно истолковывать как матрицу смежности орграфа, и тогда условия графичности пары векторов станут условиями существования ориентированного графа с заданными списками полустепеней исхода и полустепеней захода вершин.
Критерий графичности пары векторов устанавливается следующей теоремой.
Теорема 5. Пара векторов
c = (c1, c2, …, cm), d = (d1, d2, …, dn) (3)
является графической тогда и только тогда, когда выполняются следующие два условия:
1) последовательность
(c1+m-1, c2+m-1, …, cm+m-1, d1, d2, …, dn) (4)
графическая;
2)
Очевидно, что пара векторов (3) реализуется двудольным графом тогда и только тогда, когда последовательность (4) реализуется расщепляемым графом, для которого (c
1+m-1, c2+m-1, …, cm+m-1) и (d1, d2, …, dn) — списки степеней вершин верхней и нижней долей соответственно. Поэтому доказываемое непосредственно вытекает из критерия расщепляемости графической последовательности.
Коснемся вопроса о реконструируемости орграфов. Гипотезу Келли — Улама для ориентированных графов можно попытаться сформулировать так же, как и для неориентированных. Но для орграфов эта гипотеза не верна.
П. Стокмейер (1977, 1981 гг.) нашел несколько семейств нереконструируемых орграфов. Одно из них состоит из сильных турниров специального вида. Два нереконструируемых турнира изображены на рис. 4. Ф. Харари и Е. Палмер доказали (1967 г.), что любой турнир, не являющийся сильным, реконструируем.
Рис. 4.
А. Рамачандран предложил новый вариант гипотезы реконструируемости для орграфов. Пусть G — ориентированный граф. Вместе с каждым подграфом Gv = G — v, v VG, будем рассматривать упорядоченную пару (d+(v), d-(v)) полустепеней исхода и захода вершины v. Орграф G назовем N-реконструируемым, если он определяется с точностью до изоморфизма набором {(Gv, d+(v), d-(v)): v VG}.
Гипотеза Рамачандрана (1981 г.). Любой орграф N-реконструируем.
Эта гипотеза пока не доказана и не опровергнута.
1.3 Пути
Пусть
М = (P1, P2,…, Pi) (5)
— какое-либо множество путей орграфа G, попарно не имеющих общих вершин. Если множества VPi вершин этих путей составляют разбиение для VG, т. е.
VG = VP1 VP2 ... VPi,
то множество путей М называется разбиением орграфа G на пути. Минимальное число l путей, составляющих разбиение орграфа G, обозначим через l(G).
Ниже фигурируют понятия числа независимости 0(G) и хроматического числа (G) орграфа G, которые для ориентированных графов определяются так же, как и для неориентированных, т. е. 0(G) = 0(Gb), (G) = (Gb).
Теорема 6. Для любого орграфа G верно неравенство l(G) 0(G)
Фиксируем некоторое разбиение (2) орграфа G на пути. Пусть N(M) = (a1, a2, …, ai), ai Рi — множество начальных вершин этих путей. Докажем более сильное утверждение:
существует такое разбиение М' орграфа G на пути, что
N(M’) N(M), |M’| 0(G)
Доказательство последнего утверждения проведем индукцией по n = |G|. Утверждение очевидно при n = 1, 2. Пусть n > 2 и утверждение верно для орграфов, порядки которых меньше n.
Вначале покажем, что, не ограничивая общности, можно считать |М|
0(G)+1. В самом деле, пусть |М| 0(G)+2. Рассмотрим орграф G1 = G —VP1. Очевидно, что 0(G1) . 0(G). По индуктивному предположению существует разбиение М1 орграфа G1 на пути с N(M1) N(M) и |М1| 0(G1) 0(G). Но тогда М' = M1 P1 — разбиение орграфа G с N(M')N(M) и |М’| 0(G)+1. Поэтому всегда можно считать, что |М| 0(G)+1.
Пусть теперь |М| = 0(G)+1. Тогда множество N(M) = (a1, a2, …, ai) не является независимым, т. е. в нем есть хотя бы одна пара смежных вершин. Предположим, что (a1, a2) AG. Если путь P1 состоит из единственной вершины a1, то объединив P1 и P2 в путь (a1, a2, …), получим нужное разбиение.
Если же путь Р = (а1, b1, ...) имеет более чем одну вершину, то рассмотрим орграф G1 = G—a1. По индуктивному предположению существует такое разбиение M1 орграфа G1 на пути, что |М1| 0(G1) 0(G) и N(M1) = {b1, a2, a3, ..., аi}. Если b1 N(M1), то М' получим из M1, добавив вершину a1 к пути, начинающемуся в b1. Аналогично можно поступить и тогда, когда а2 N(M1). Если же b1 N(M1) и a2 N(M1), то М' = M1 {(a1)}.
Из теоремы 6 вытекают два важных следствия.
Орграф G называется транзитивным, если истинна импликация
((x, y) AG и (y, z) AG) (x, z) AG
Следствие 7. Если орграф G транзитивен, то l(G) = 0(G).
Согласно предыдущей теореме l(G) 0(G). Но две вершины транзитивного орграфа, принадлежащие одной цепи, смежны, поэтому 0(G)l(G). Итак, l(G) = 0(G).
Следствие 8. В каждом турнире существует гамилътонов путь.
Поскольку любые две вершины, произвольного турнира Т смежны, то 0(T)=1. Поэтому существует цепь Р, содержащая все вершины турнира Т.
Для сильных турниров верно следующее более общее утверждение.
Теорема 9. Пусть Т — сильный турнир порядка n. Тогда для любой его вершины u и для любого числа k, 3 k n, в Т есть контур длины k, содержащий вершину u.
Пусть S (u) и Р(u) — множество всех тех вершин v и, соответственно, w турнира Т, для которых (u, v) AT и (w, u) АТ. Оба эти множества не являются пустыми, поскольку орграф Т сильный. По той же причине существует хотя бы одна дуга (v, w), идущая из S (u) в Р(u) (рис. 5). Следовательно, вершина и лежит на контуре длины 3.
Далее воспользуемся индукцией по k. Пусть вершина u входит в контуры всех длин от 3 до k, где k < n. Покажем, что она входит в контур длины k + 1.
Пусть С=(v0, v1, …, vk), v0 = vk = u, — контур длины k. Предположим, что для некоторой вершины w, не входящей в этот контур, существуют такие дуги (w, x) и (у, w), что x VC и у VC. Тогда в С есть такие две смежные вершины vi, и vi+1, что (vi, w) и (w, vi+1)—дуги турнира Т.
Следовательно, вершина u входит в контур
С=(v0, v1, …, vi, w, vi+1, …, vk)
v0 = vk = u
длины k + 1.
Рис. 5.
Если же указанной выше вершины w нет, то множество вершин турнира Т, не входящих в контур С, можно разбить на две части S (С) и Р(С) так, чтобы для любых вершин aS(C), bP(C) и v С выполнялись условия (v, а) AG и (b, v) AG. Так как орграф T сильный, то S(С) и Р(С) не пусты и существует дуга, идущая из некоторой вершины a S(С) в некоторую вершину b Р(С) (рис. 6). Таким образом, вершина u входит в контур
С‘ = (v0, a, b, v2, …, vk)
длины k + 1.
Очевидно
Следствие 10. Сильный турнир гамильтонов. Заметим, что предыдущее следствие вытекает также из теоремы 9.
Теорема 11. Если k—максимальная длина путей в орграфе G, то (G).k + 1.
Обозначим через В такое минимальное относительно включения подмножество в АG, что орграф G1 = G — В не имеет контуров. Для любой вершины v определим t(v) как число вершин пути в орграфе G1 с началом в v, имеющем максимальную длину. Приписав каждой вершине v цвет t(v), получим раскраску орграфа G не более чем k + 1 цветами. Остается доказать, что эта раскраска правильная, т. е. что t(u) t(v) для любых двух смежных вершин u и v. Но если (u, v) АG1, то t(u)>t{v). Если же (u, v) В, то G1+(u,v) имеет контур. Поэтому в G1 существует (v, u) - путь и, следовательно, t(v)>t(u).
Итак, доказано, (G).k + 1.
Рис. 6.
2. Описание алгоритма
Матрицей достижимости графа с n вершинами называется квадратная матрица R порядка n, элементы которой определяются следующим образом:

Матрицей контрдостижимости графа с n вершинами называется квадратная матрица Q порядка n, элементы которой определяются следующим образом:

Матрицей сильной связности орграфа с n вершинами называется квадратная матрица S порядка n, элементы которой определяются следующим образом:

При машинной реализации алгоритмов на графах матрицы расстояний, достижимости, контрдостижимости и сильной связности можно определять через матрицу смежности.
Пусть дан граф G,
Пример. Дан граф G (рис. 7). Найти матрицу расстояний D.

Рис. 7
Сначала найдем матрицу смежности A, элемент aij которой равен 1, если вершины xi и xj графа G смежны, и равен нулю в противном случае. В матрице D диагональные элементы будут равны нулю, так как расстояние между вершинами xi и xj, если i = j, считается равным нулю. Если элемент aij матрицы A равен 1, то соответствующий элемент dij матрицы D тоже будет равен 1. Недоопределенная матрица D изображена ниже.
Умножим матрицу А саму на себя по правилу умножения матриц и найдем матрицу A2.
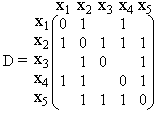
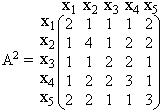
Так как в матрице A2 нет нулевых элементов, то оставшиеся неопределёнными элементы матрицы D равны 2. Окончательно матрица D будет иметь вид:
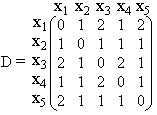
Матрицу достижимости R можно найти с помощью матрицы смежности А следующим образом R = T(E+A+A2+...+An-1), где n число вершин, E единичная матрица, а оператор T определяется следующим образом:

Матрица контрдостижимости Q находится транспонированием матрицы достижимости R: Q = R
