ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.10.2024
Просмотров: 11
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3. Уравнения, каких "элементарных" процессов входят в математическое описание?
В составе математического описания, разработанного на основе физической природы исследуемого объекта, можно выделить следующие группы уравнений:
1. Уравнения баланса масс и энергии, записанные с учетом гидродинамической структуры движения потоков. Данная группа уравнений характеризует распределение в потоках температур, составов и связанных с ними свойств: плотности, теплоемкости и т.д.
2. Уравнения кинетики процессов. Сюда относятся описания элементарных процессов протекания химической реакции, теплопереноса, массопереноса. Для записи уравнений используются гипотезы дополнительных связей между основными переменными процесса.
3. Теоретические, эмпирические или полуэмпирические соотношения между различными параметрами процесса – уравнения для физических или гидродинамических параметров: теплоемкости, вязкости, коэффициентов теплоотдачи и т.д.
4. Ограничения на параметры процесса, например, температура в зоне катализатора не может быть выше некоторой заданной, иначе катализатор потеряет свои свойства и т. д.
Данные группы уравнений входят в состав математической модели любого химико-технологического процесса. Они представляют аналитическую теорию исследования физико-химических процессов. Кроме того, модель строится так, чтобы она наиболее полно отражала характер поведения потоков вещества и энергии при одновременно достаточно простом математическом описании. Простота математического описания определяется возможностью решения модели на ЭВМ.
4. Что такое модель идеальное смешения?
По модели идеального смешения поток представляется в виде непрерывной среды, которая поступает в аппарат и мгновенно распределяется по всему объему аппарата вследствие полного (идеального) перемешивания частиц потока, при этом концентрация и температура остаются постоянными во всех точках объема данного аппарата и на выходе из него при постоянном объеме.
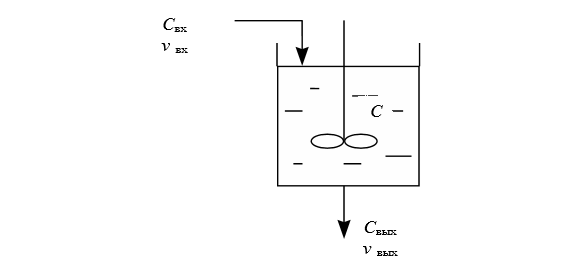
5. Что такое модель идеального вытеснения?
Модель идеального вытеснения – это модель с идеализированной структурой потока, в котором принимается поршневое течение без перемешивания вдоль потока при равномерном распределении концентраций вещества в направлении, перпендикулярном движению потока:
Здесь - линейная скорость потока на входе и выходе из аппарата, м/с.
6. Чем отличаются диффузионные модели от моделей идеального вытеснения?
Диффузионные модели применяют при описании реальных потоков в аппаратах, в которых происходит продольное и радиальное перемешивание веществ. Природа возникновения продольного и радиального перемешивания весьма сложна. Предположим, что перемешивание в потоке идеального вытеснения (конвективный поток) возникает за счет молекулярной диффузии.
7. Для каких аппаратов может быть применена ячеечная модель?
Физическая сущность ячеечной модели заключается в том, что материальный поток может быть представлен несколькими последовательно соединенными ячейками, при этом допускается, что в каждой ячейке поток имеет структуру идеального смешения, а между ячейками перемешивание отсутствует.
Ячеечные модели достаточно точно отражают свойства потоков в различных абсорбционных и экстракционных колоннах, в теплообменных аппаратах некоторых конструкций, в каскаде химических реакторов с мешалками, в аппаратах с псевдоожиженным слоем.
8. Что такое время пребывания частицы в аппарате?
Время пребывания вещества в каждой ячейке
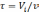
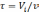, общее время пребывания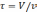 
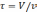, тогда объем всех ячеек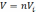 
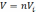, где n - число ячеек.9. Для чего используются допущения при составлении математического описания?
Точное определение полного числа невыявленных ошибок в комплексе программ прямыми методами измерения невозможно. Однако имеются пути для приближенной статистической оценки их полного числа или вероятности ошибки в каждой команде программы.
10. Какие группы допущений вы знаете?
Описаны несколько математических моделей, основой которых являются различные гипотезы о характере проявления вторичных ошибок в программах. Эти гипотезы в той или иной степени апробированы при обработке данных реальных разработок, и их можно разделить на три группы. Такие оценки базируются на построении математических Моделей в предположении о жесткой корреляции между общим количеством и проявлениями ошибок в комплексе программ после его отладки в течение времени T.
11. Какие допущения входят в каждую группу?
В первую группу входят очевидные допущения, статистическая проверка которых невозможна и нецелесообразна. Вторую группу составляют допущения, определяющие специфические характеристики модели и требующие статистической проверки и обоснования на базе экспериментальных исследований. В третью группу включены второстепенные допущения, расширяющие и уточняющие возможности применения модели и частично доступные экспериментальной проверке.
1 Оставить нужное