Введение

Понятие функции является одним из основных понятии математики. Идея определить функциональную зависимость, к примеру, изменения площади или объема фигуры в зависимости от изменения ее размеров относят еще к древнегреческой математике.

В то время самым же большим достижением в математике справедливо считается изобретение в XVII веке дифференциального и интегрального исчисления. Сформировалось оно Ньютоном и Лейбницем (впервые термин "функция" Лейбниц вводит в рассмотрение в 1694 г).

Введение в математику методов анализа бесконечно малых величин стало началом больших преобразований. Вырабатывались элементы будущего дифференциального исчисления при решении задач, которые в настоящее время решаются только с помощью дифференцирования.

Современный экономист должен хорошо владеть количественными методами анализа. Математика является не только орудием количественного расчета, но также методом точного исследования. Она служит средством предельно четкой и ясной формулировки экономических понятий и проблем.

Понятие производной

Сразу дадим определение производной, как оно сформулировано в учебниках математики:

Производная функции – это отношение приращения функции к приращению аргумента при бесконечно малом приращении аргумента.

При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f(x) получать новую функцию, которую называют производной функцией (или просто производной) данной функции f(x) и обозначают символом:



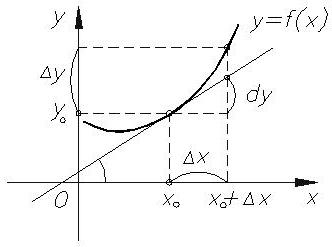
Приращением в математике называют изменение. То, насколько изменился аргумент (x) при продвижении вдоль оси Ox, называется приращением аргумента и обозначается Δx. То, насколько изменилась функция (высота) при продвижении вперед вдоль оси Ox на расстояние Δx, называется приращением функции и обозначается Δy.

Действие нахождения производной называется её дифференцированием, а функцию, имеющую производную в точке х, называют дифференцируемой в этой точке т.е. предел Δy/Δx в даной точке существует и конечен.

---

Функция, дифференцируемая в каждой точке промежутка, называется дифференцируемой в этом промежутке.



Итак, производная функции f(x) – это отношение Δf к Δx при Δx→0. Производная обычно обозначается той же буквой, что и функция, только со штрихом сверху справа: f'(x) или просто f​′​​. Итак, запишем формулу производной, используя эти обозначения:

f′(x)=Δf/Δx при Δx→0

при возрастании функции производная положительна, а при убывании – отрицательна.

Производная  характеризует скорость изменения функции

В физическом смысле производная - это скорость изменения функции. Производная функции изменения координаты - это скорость движения, производная функции скорости является ускорением. Таким образом, зная формулу изменения координат тела в пространстве, можно найти его скорость и ускорение в каждой координате пространства.

При возрастании функции производная положительна, а при убывании – отрицательна.

Применение производной в экономике

Применение производной в экономике позволяет получать так называемые предельные характеристики экономических объектов или процессов. Предельные величины (предельная выручка, полезность, производительность, предельный доход, продукт и др.) характеризуют не состояние, а скорость изменения экономического объекта или процесса по времени или относительно другого исследуемого фактора, что подразумевает под собой вычисление (нахождение) производной.

В экономической теории используется понятие «маржинальный», что означает «предельный». Введение этого понятия позволило создать совершенно новый инструмент исследования и описания экономических явлений. Классическая экономическая теория имела дело со средними величинами: средняя цена, средняя производительность труда и т.д. Но существенные закономерности оказалось можно обнаружить в области предельных величин.

---

Экономический смысл производной: первая производная от объема произведенной продукции в определенный момент времени есть производительность труда. Это производственная функция Кобба-Дугласа. Иными словами: при увеличении числа рабочих, частная производная от производственной функции будет равна добавочной стоимости продукции, произведенной еще одним дополнительным рабочим. По этой причине это частное приращение называется предельной производительностью труда.

Функцию, выражающую зависимость между стоимостью выпускаемой продукции и стоимостью суммарных затрат на её производство, называют производственной функцией.

Производственная функция Кобба-Дугласа (Cobb-Douglas production function) — модель, показывающая зависимость объёма производства (Q) от создающих его факторов производства — труда (L) и капитала (K).

Впервые была предложена Кнутом Викселем, но проверена лишь в 1928 г. американскими экономистами Чарльзом Коббом и Полом Дугласом.

Функция имеет следующий вид:

Q = A × L^α × K^β

где Q — объем производства; L — труд; K — капитал; A — технологический коэффициент; α — коэффициент эластичности по труду; β — коэффициент эластичности по капиталу.

Коэффициент эластичности. Эласти́чность (англ. elasticity) — численная характеристика изменения одного показателя (например: спроса или предложения) к другому показателю (например: цене, доходу) и показывающая, на сколько процентов изменится первый показатель при изменении второго на 1%.

Также с помощью экстремума функции (производной) в экономике можно найти наивысшую производительность труда, максимальную прибыль, максимальный выпуск и минимальные издержки.

При увеличении числа рабочих, частная производная от производственной функции будет равна добавочной стоимости продукции, произведенной еще одним дополнительным рабочим.

Предельная себестоимость характеризует отношение прироста себестоимости к приросту объема продукции при малом изменении продукции.

Производная выступает как скорость изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора.

Экономический смысл производной.

Пусть предприятие «А» производит Х единиц продукции.

---

К - суммарные затраты или издержки производства.

Производственная функция, описывающая зависимость затрат от объёма производства имеет вид: К=f(х).

Увеличим производство на ,тогда затраты вырастут на

Среднее приращение затрат будет равно:



Теперь рассмотрим понятие предельных издержек производства:

Предельные издержки производства – это дополнительные затраты, которые несёт предприятие при увеличении объёма производства на бесконечно малую величину.

А это не что иное, как предел среднего приращения затрат при стремлении к нулю.



Именно таким образом вычисляется значение производной функции в точке.

Значение производной функции в данной точке есть предельные издержки производства при данном его объёме.

Пример 1

Расчет производительности труда:

Объем продукции, произведенной цехом, может быть описан уравнением:

u= - t³+5t²+120t+10, где 1≤t≤8 — рабочее время (ч).

Необходимо вычислить производительность труда и скорость ее изменения в момент t=1 и t=4.

Производительность труда найдем по формуле:

z(t)=lim = u'(t) dt – 0

z(t) = u'(t)= -3t²+10t+120 (eд./ч).

Скорость изменения производительности труда вычислим как производную: z'(t) = -6t+10 (ед./ч 2 )

Тогда в заданные моменты времени имеем:

z(1) =128 (ед./ч 2 ),

z'(1)= 4 (ед./ч 2 );

 z(4) = 112 (ед./ч 2 ),

z'(4)=-14(ед./ч2).

Из вычислений можно сделать вывод, что производительность труда к концу рабочего дня снижается.

При этом изменение знака в z'(t) свидетельствует о том, что увеличение производительности труда в первые часы рабочего дня смещаются ее снижением в последующие часы. Такой результат является следствием усталости работников, ухудшением условий в помещении и множества других факторов, влияющих на производительность труда.

Пример 2

Рассмотрим производственную функцию у=f(х), которая представляет собой зависимость объёма производимой продукции от объёма затраченного ресурса х

---

. Пусть этот ресурс – это количество человеческого труда, выраженного в человеко-часах или числе работников.

Пусть в некоторый момент времени число работников фирмы равно а. Возникает вопрос о целесообразности принятия на работу ещё одного рабочего т. е оценить разность f(а+Δа)-f(а), при Δа=1.

Поскольку мы считаем, что производственные функции дифференцируемы, то f(а+1)-f(а) ≈ f´(а). Если а велико, то это равенство довольно точное. Тогда f´(а)- добавочная продукция, производимая новым сотрудником (добавочная стоимость продукции). Пусть С – цена единицы продукции, а р зарплата работника. Тогда, если С*f´(а) > р, то надо нанять ещё одного работника, т. к. он принесёт фирме больше, чем она ему заплатит.

Таким образом, чтобы увеличить производство необходимо:

1. 
   Увеличивать производительность труда путем улучшения условий труда, применением более современных орудий труда, принятием на работу большего количества работников;
   
2. 
   Упростить операции при производстве. Однако здесь надо очень тщательно рассчитывать параметры изменения качества продукции, т.к., при значительном снижении качества продукции можно сильно потерять в продажах и значительно увеличить имиджевые риски;
   
3. 
   Принять на работу дополнительных работников.
   

Дополнение:

Один из базовых законов теории производства звучит так: "Оптимальный для производителя уровень выпуска товара определяется равенством предельных издержек и предельного дохода".

Издержки производства y представляют собой в общем виде функцию количества выпускаемой продукции х(Q). Если Δx - прирост продукции, тогда Δy – приращение издержек производства и Δx/Δy - среднее приращение издержек производства на единицу продукции. Производная y΄ = выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство единицы дополнительной продукции: J(x) = y΄ (x) (МС = ТС`).

---

Смотрите также файлы

• Практическое задание 3, Модуль Организация и управление в логистике Преподаватель.pdf

• Мобильных приложений.docx

• Конспект по изучаемой теме. В конспекте должны быть отражены следующие моменты временные рамки возраста.docx

• Инструкция для слушателя по работе в системе дистанционного обучения.docx

• Анализатора Функция зрения осуществляется благод.docx