ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.10.2024
Просмотров: 14
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| ||||||||||||||
Раздел Общая теория статистики
Тема Абсолютные и относительные величины
По данным таблицы рассчитать поквартально проценты установленного планового задания и проценты выполнения плана по выпуску продукции; Расчетные данные оформить в таблице.
| Кварталы | Выпуск продукции, млн. руб. | Процент выполнения плана | Процент планового задания | ||
| Базисный период | Отчетный период | ||||
| план | факт | ||||
| I | 22,25 | 22,28 | 24,15 | 108,4 | 100,1 |
| II | 21,30 | 21,35 | 23,62 | 110,6 | 100,2 |
| III | 22,30 | 22,94 | 23,93 | 104,3 | 102,7 |
| IV | 22,20 | 22,29 | 24,08 | 108 | 100,4 |
Вычислим показатели выполнения плана за соответствующий квартал:
Процент выполнения плана = (фактический выпуск продукции/ плановый выпуск продукции) x100%
По расчетам можно сделать следующие выводы: более высокий процент перевыполнения плана по выпуску продукции приходится на II квартал (110,6%). В III квартале план был перевыполнен лишь на 4,3% (104,3 - 100).
Относительные величины планового задания - показатели, характеризующие степень установления планового задания на отчетный период. Рассчитываются по формуле:
Процент планового задания = (плановые данные на отчетный период/Фактические данные за базисный период) x100%
По расчетам можно сделать следующие выводы: более высокий процент установления планового задания приходится на III квартал - 102,7%, в то время как на I квартал всего лишь 100,1%, на II квартал - 100,2%, на IV квартал - 100,4%.
Тема Средние величины
По данным таблицы рассчитать средний стаж работника
| Группы работников по общему стажу работы, лет | Численность работников, чел. (m) |
| до 5 | 18 |
| 5-10 | 40 |
| 10-15 | 15 |
| свыше 15 | 10 |
| | |
| Итого | 83 |
Средний стаж работника составит:
(2,5x18+7,5x40+12,5x15+17,5x10)/83=8,5 года
Тема Показатели динамики
По данным выпуска товарной продукции рассчитать аналитические показатели динамики и заполнить таблицу
| Месяцы | Выпуск товарной продукции, тыс. руб. | Показатели динамики | ||||||
| Абсолютный прирост (), тыс. руб. | темп роста, % (Тр) | темп прироста, % (Тпр) | Абсолютное значение 1% прироста, тыс. руб. (А) | |||||
| Цепной | Базисный | цепной | базисный | |||||
| 1 | 236 | - | - | 100,0 | - | - | - | |
| 2 | 244 | 8 | 103,4 | 103,4 | 3,4 | 3,4 | 2,4 | |
| 3 | 246 | 2 | 100,8 | 104,2 | 0,8 | 4,2 | 2,5 | |
| 4 | 249 | 3 | 101,2 | 105,5 | 1,2 | 5,5 | 2,5 | |
| 5 | 250 | 1 | 100,4 | 105,8 | 0,4 | 5,9 | 2,5 | |
| 6 | 252 | 2 | 100,8 | 106,8 | 0,8 | 6,8 | 2,5 | |
Абсолютный прирост (Л) определяется как разность между отчетным и предыдущим уровнями ряда динамики, т.е. по формуле
Δ= уi – yi-1,
где уi - уровни ряда динамики (численные значения ряда динамики).
Абсолютный прирост характеризует абсолютное изменение явления в отчетном периоде по сравнению с предыдущим. Например, абсолютный прирост продукции в феврале по сравнению с январем составил Δ 2=244 - 236=8 тыс.руб., а в марте по сравнению с февралем Δ 3=246 - 244=2 тыс.руб. и т.п. Результаты расчетов сведены в таблице.
Как видно из расчетных данных, наиболее значительно возрос объем продукции в феврале - на 8 тыс. руб., в то время как в мае абсолютный прирост продукции составил всего 1 тыс. руб.
Средний абсолютный прирост (Δ) определяется на основе данных абсолютных приростов по следующим формулам:
Δ=ΣΔ/n-1 или (yn-y1)/n-1,
где п - число уровней ряда динамики;
У1 и Уп - соответственно первый и последний абсолютные уровни ряда динамики.
Средний абсолютный прирост за рассматриваемый период динамики составит:
Δ=(8 + 2 + 3 +1 + 2)/(6-1)=3.2 тыс.руб
Δ=(252-236)/(6-1)=3.2 тыс.руб
Таким образом, за рассматриваемый период прирост продукции в среднем составил 3,2 млн. руб.
Темп роста (Тр) определяется по формуле:
Tp = (y1/y0)x100%,
где у0 - уровень ряда динамики, взятый за базу сравнения.
Темп роста характеризует относительный рост явления за рассматриваемый период.
Темпы роста рассчитываются по принципу цепных и базисных соотношений. В том случае, когда за базу сравнения принимается предыдущий период, рассчитываются цепные показатели темпа роста; когда сравнение осуществляется с любым другим уровнем ряда динамики, взятым за базу сравнения, рассчитываются базисные темпы роста.
Так, в феврале по сравнению с январем выпуск продукции составил Тр2 = (244:236)-100% = 103,4%, а в марте по сравнению с февралем Тр3 = (246:244)-100% = 100,8% и т.п.
Результаты расчетов цепных темпов роста см. в табл.
Как видно, наиболее значительно возрос объем продукции в феврале (Тр2 = 103,4%), менее всего увеличился объем продукции в мае (Тр5 = 100,4%).
Если за базу сравнения взять январь, то выпуск продукции в марте по сравнению с январем составил Тр3 = 104,3%, а в апреле по сравнению с январем - 105,5% и т.п. Результаты расчетов базисных темпов роста сведем в табл. 1.
Как видно из расчетных данных, базисные показатели темпов роста резко отличаются от цепных. Так, в июне по сравнению с маем темп роста выпуска продукции составил 100,8%, а по сравнению с январем - 106,8%. Аналогичные сравнения можно провести и по другим месяцам.
Темп прироста (Тпр) характеризует относительный прирост явления за рассматриваемый период. Темп прироста определяется по формуле:
Тпр = Тр - 100%.
Так же, как и темпы роста, темпы прироста бывают цепные и базисные.
Цепные темпы прироста составят:
в феврале - Тпр2 = 3,4% (103,4 - 100), в марте - Тпр3 = 0,8% (100,8 - 100) и т.п.
Базисные темпы прироста составят:
в феврале - Тпр2 = 3,4% (103,4-100),
в марте - Тпр3 = 4,2% (104,2 - 100) и в апреле Тпр4 = 5,5% (105,5 - 100) и т.п.
Из расчетных значений цепных темпов прироста ясно, что наиболее значительно увеличился объем выпуска продукции в феврале - на 3,4% (103,4 - 100), а менее всего - в мае - на 0,4%
(100,4-100). Базисный темп роста за июнь характеризует увеличение объема выпуска продукции за первое полугодие на 6,8% (106,8 - 100).
Абсолютное значение одного процента прироста (А) характеризует абсолютный эквивалент одного процента прироста и
определяется по формуле:
A = Δ/Tпр.
Так, в феврале абсолютное значение одного процента прироста составило А2 = (8:3,4) = 2,4 млн. руб.; в марте - А3 = (2:0,8) = 2,5 млн. руб. и т.п.
Средний темп роста (Х) за период динамики определяют по формуле средней геометрической на основе данных цепных коэффициентов динамики либо на основе данных абсолютных уровней ряда динамики по формулам:
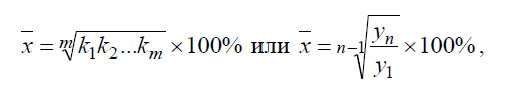
где ki,k2,...km - коэффициенты динамики по отношению к
предыдущему периоду;
m - число коэффициентов динамики;
n - число абсолютных уровней ряда динамики;
у1 и yn - соответственно первый и последний абсолютные уровни ряда динамики.
За первое полугодие средний годовой темп роста продукции составил
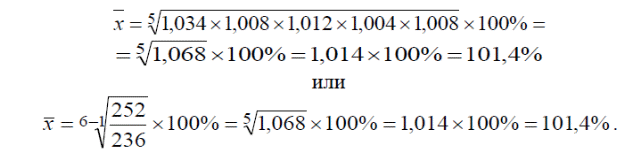 ,
,Таким образом, за рассматриваемый период объем выпуска продукции возрос в среднем на 1,4%.
Тема Индексы
По данным таблицы рассчитать сводные индексы стоимостного объема продукции, физического объема продукции и цен.
Исходные данные
| Виды продукции | Количество произведенной продукции, тыс. шт. | Цена 1 шт., тыс. руб. | ||
| базисный период (q0) | Отчетный период (q1) | базисный период (p0) | отчетный период (p1) | |
| А | 4402 | 4452 | 0,6 | 0,5 |
| Б | 1248 | 1150 | 1,2 | 0,8 |
Рассчитаем индивидуальные индексы продукции и индивидуальные индексы цен.
Индивидуальные индексы по соответствующим видам продукции составят:
iq(А) =q1/q0 = (4452/4402) x100% =101,1%
iq(Б) =q1/q0 = (1150/1248) x100% =92,1% ,
т.е. в отчетном периоде по сравнению с базисным произведено продукции вида А на 1,1% (101,1 – 100) больше, а вида Б на 7,9% меньше (92,1 – 100).
Индивидуальные индексы цен по соответствующим видам продукции составят:
ip(А) =P1/P0=(0.5/0.6) x100 = 83,3%
ip(Б) =P1/P0=(0.8/1.2) x100 =66,7%,
т.е. цена единицы продукции вида А в отчетном периоде по сравнению с базисным снизилась на 16,7% (83,3 – 100), вида Б снизилась на 33,3% (66,7 – 100). Индивидуальные индексы конкретного вида продукции в стоимостном выражении, соответственно, составят:
iqp(А) 100% 84,3%
iqp(Б) 100% 61,4%
Таким образом, объем продукции в стоимостном выражении вида А в отчетном периоде по сравнению с базисным снизился на 15,7% (84,3-100), вида Б –на 38,6% (61,4 – 100).
Для того чтобы ответить на вопрос, как изменился объем всей продукции предприятия в отчетном периоде по сравнению с базисным, необходимо рассчитать сводные индексы продукции, цен и физического объема продукции.
Сводный индекс объема продукции в стоимостном выражении составит:
Iqp= Σq1p1/ Σq0p0 =((4452x0.5+1150.8)/(4402x0.6+1248x1.2))x100%=76%
Сводный индекс цен составит:
I p= Σq1p1/ Σq1p0 =((4452x0.5+1150.8)/(4402x0.6+1150x1.2))x100%=77.7%
Сводный индекс объема продукции составит:
Iq Σq1p0/ Σq0p0 =((4452x0.6+1150.8)/(4402x0.6+1248x1.2))x100%=97.9%
Используя первое свойство индексов, имеем:
Iqp = Iq·Ip; 76%=0,777x0,979x100%.
Используя второе свойство индексов, имеем:
Δqp(qp) =Δqp(q)+ Δqp(p), т.е.
(3146 – 4138,8) = (4051,2 – 4138,8) + (3146 – 4051,2)
или
–992,8 = –87,6 – 905,2.
Таким образом, можно сделать вывод: объем продукции в стоимостном выражении уменьшился в целом на 24% (76,0 – 100), или на 992,8 тыс. руб. (3146 – 4138,8); в том числе за счет снижения цен на 22,3 % (77,7 – 100) объем продукции в стоимостном отношении выражении снизился на 905,2 тыс. руб. (3146 – 4051,2) и за счет снижения физического объема продукции на 2,1 % (97,9- 100) объем продукции в стоимостном выражении уменьшился на 87,6 тыс. руб. (4051,2 – 4138,8).
Тема Графическое изображение статистических данных
По данным таблицы построить графики динамики в виде линейной и столбиковой диаграмм
| Месяцы | Выпуск продукции, млн. руб. | Месяцы | Выпуск продукции, Млн.руб. |
| Январь | 18,6 | Июль | 19,6 |
| Февраль | 17,3 | Август | 17,5 |
| Март | 18,9 | Сентябрь | 19,2 |
| Апрель | 19,2 | Октябрь | 19,8 |
| Май | 17,9 | Ноябрь | 18,3 |
| Июнь | 19,1 | Декабрь | 19,4 |

