Файл: Решение квадратного уравнения Используется для нахождения корней многочлена второй степени вида f.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.10.2024
Просмотров: 17
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 x 1 2
x 1 22
X2 root d f (x) x
x 1.5
X2 1.414
dx
f (X2) 3.657
-
Решение систем линейных алгебраических уравнений
Известно, что система линейных уравнений в матричной форме A∙X=B. Вектор решения получается из X=A-1∙B.
Для решения систем линейных уравнений в MathCAD существует встро- енная функция lsolve(A,B), которая возвращает вектор X для системы линейных уравнений при заданной матрице коэффициентов и векторе свободных членов.
Также используются системы линейных уравнений для вычисления оп- ределителя по формулам Крамера – точный метод решения. Решение линейной системы методом Гаусса – приближенный метод.
Функции, предназначенные для решения задач линейной алгебры, можно разделить на три группы:
-
функции определения матриц и операции с блоками матриц; -
функции вычисления различных числовых характеристик матриц; -
функций, реализующие численные алгоритмы решения задач линейной алгебры.
Пример:
Решить систему линейных уравнений:
x2 y3z1
2 x3 y z2
x2 y5z3
-
Преобразуем данную систему:
1x2 y3z1
2 x3 y1z2
1x2 y5z3
-
Матрица коэффициентов системы:

 1 2 3
1 2 3 A 2 3 1
A 2 3 11 2 5
-
Вектор свободных членов

 1
1 b 2
b 23
-
Решение системы

 X A 1.b
X A 1.b-
Результаты решения

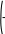 8
8X = 5
1
-
Проверка решения

 0
0 A.X b = 0
A.X b = 00
-
Решение с применением функции Isolve

 X lsolve( A, b)
X lsolve( A, b)
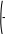 8
8X = 5
1
-
Решение системы линейных уравнений по формулам Крамера
Порядок выполнения
-
Переменной ORIGIN присвоить значение равное единице. -
Ввести матрицу коэффициентов системы. -
Ввести вектор свободных членов (столбец правых частей). -
Вычислить определитель матрицы системы. Система имеет единст- венное решение, если определитель отличен от нуля. -
Вычислить определителей матрицы, полученных заменой соот- ветствующего столбца столбцом правых частей. -
Определить решение системы по формулам Крамера.
Пример:
Решить систему линейных уравнений:
x2 y3z1
2 x3 y z2
x2 y5z3
-
Преобразуем данную систему:
1x2 y3z1
2 x3 y1z2
1x2 y5z3
-
Матрица коэффициентов системы:

 1 2 3
1 2 3 A 2 3 1
A 2 3 11 2 5
-
Вектор свободных членов

 1
1 b 2
b 23
-
Присваиваем переменной ORIGIN значение 1.
 ORIGIN 1
ORIGIN 1-
Вычисляем определителя матрицы системы.



 A = 2
A = 2-
Вычисление определителей матрицы

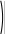 1 2 3
1 2 3 1 2 3 1
1 2 3 13 2 5
1 1 3

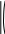
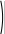 2 2 2 1
2 2 2 11 3 5
1 2 1

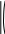
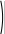 3 2 3 2
3 2 3 21 2 3
 1 = 16
1 = 162 = 10
3 = 2
-
 Определение решения системы по формулам Крамера
Определение решения системы по формулам Крамера
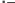 x 1
x 1
y 2


z 3
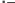
x = 8
y = 5
z = 1
-
Решение линейной системы методом Гаусса (метод гауссовых ис- ключений)
Порядок выполнения:
-
Переменной ORIGIN присвоить значение равное единице. -
Ввести матрицу системы и вектор-столбец правых частей. -
Сформировать расширенную матрицу системы при помощи функции
augment(A,b).
-
Привести расширенную матрицу системы к ступенчатому виду при помощи функции rref(Ar). -
Сформировать столбец решений системы при помощи функции sub- matrix(Ag,1,3,4,4).
Пример:
Решить систему линейных уравнений:
x2 y3z1
2 x3 y z2
x2 y5z3
-
Преобразуем данную систему:
1x2 y3z1
2 x3 y1z2
1x2 y5z3
-
Матрица коэффициентов системы:

 1 2 3
1 2 3
A 2 3 1
1 2 5
-
Вектор свободных членов

 1
1 b 2
b 23
-
Присваиваем переменной ORIGIN значение 1.
 ORIGIN 1
ORIGIN 1-
Формирование расширенной матрицы системы
 Ar augment(A, b)
Ar augment(A, b)Ar =
1 2 3 1

 2 3 1 2
2 3 1 21 2 5 3
-
Приведение расширенной матрицы системы к ступенчатому виду
 Ag rref( Ar )
Ag rref( Ar )Ag =
1 0 0 8


 0 1 0 5
0 1 0 50 0 1 1
-
Формирование столбца решения системы

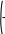 8
8
 x submatrix( Ag , 1, 3, 4, 4)
x submatrix( Ag , 1, 3, 4, 4)x = 5
1
-
Решения нелинейных уравнений
-
Решение трансцендентных уравнений
Многие уравнения, например трансцендентные, не имеют аналитических решений. Однако они могут решаться численными методами с заданной по- грешностью. Для простейших уравнений вида F(x)=0 решение находится с по- мощью функции root. Эта функция возвращает значение переменной с указан- ным уровнем, при котором выражение дает 0.
Пример:
Решить уравнение 3-ей степени:
x3 6x2 21x 52 0
-
Ввод коэффициентов полинома.



 a3 1 a2 6 a1 21 a0 52
a3 1 a2 6 a1 21 a0 52-
 Ввод полинома.
Ввод полинома.

