Федеральное государственное автономное

образовательное учреждение

высшего образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Институт Инженерной Физики и Радиоэлектроники


ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №3

АНАЛИЗ СПЕКТРАЛЬНЫХ И КОРРЕЛЯЦИОННЫХ ХАРАКТЕРИСТИК СИГНАЛОВ НА ОСНОВЕ

ДИСКРЕТНОГО (БЫСТРОГО) ПРЕОБРАЗОВАНИЯ ФУРЬЕ
Вариант 10

Преподаватель ________ Глинченко А. С.

^{подпись, дата}
Студент РФ 13-35Б 051314825 ________ Мустафаев Р.В.

^{подпись, дата}

Красноярск 2016

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №3

Анализ спектральных и корреляционных характеристик сигналов на основе

дискретного (быстрого) преобразования Фурье
ЦЕЛЬ ЛАБОРАТОРНОЙ РАБОТЫ
Целью работы является практическое изучение и освоение методов и программных средств спектрально-корреляционного анализа сигналов, основанного на дискретном (быстром) преобразовании Фурье (ДПФ-БПФ).

ИСХОДНЫЕ ДАННЫЕ
Таблица 1 – Исходные данные для выполнения лабораторной работы в

соответствии с номером варианта

Вариант	10
Частота дискретизации fд, кГц	144
Центральная частота канала f0, кГц	42
Частота среза 1 ППФ, кГц	40.3
Частота среза 2 ППФ, кГц	43.7
Частота задержки 1 ППФ, кГц	39.7
Частота задержки 2 ППФ, кГц	44.3
Номинальный шаг анализа по частоте, кГц	1
Номинальная ширина окна анализа	144

Таблица 1
Ход работы.
Задание 1. Анализ амплитудного и фазового спектров сигналов. Исследование спектральной утечки и интерполяции при спектральном анализе на основе ДПФ

---

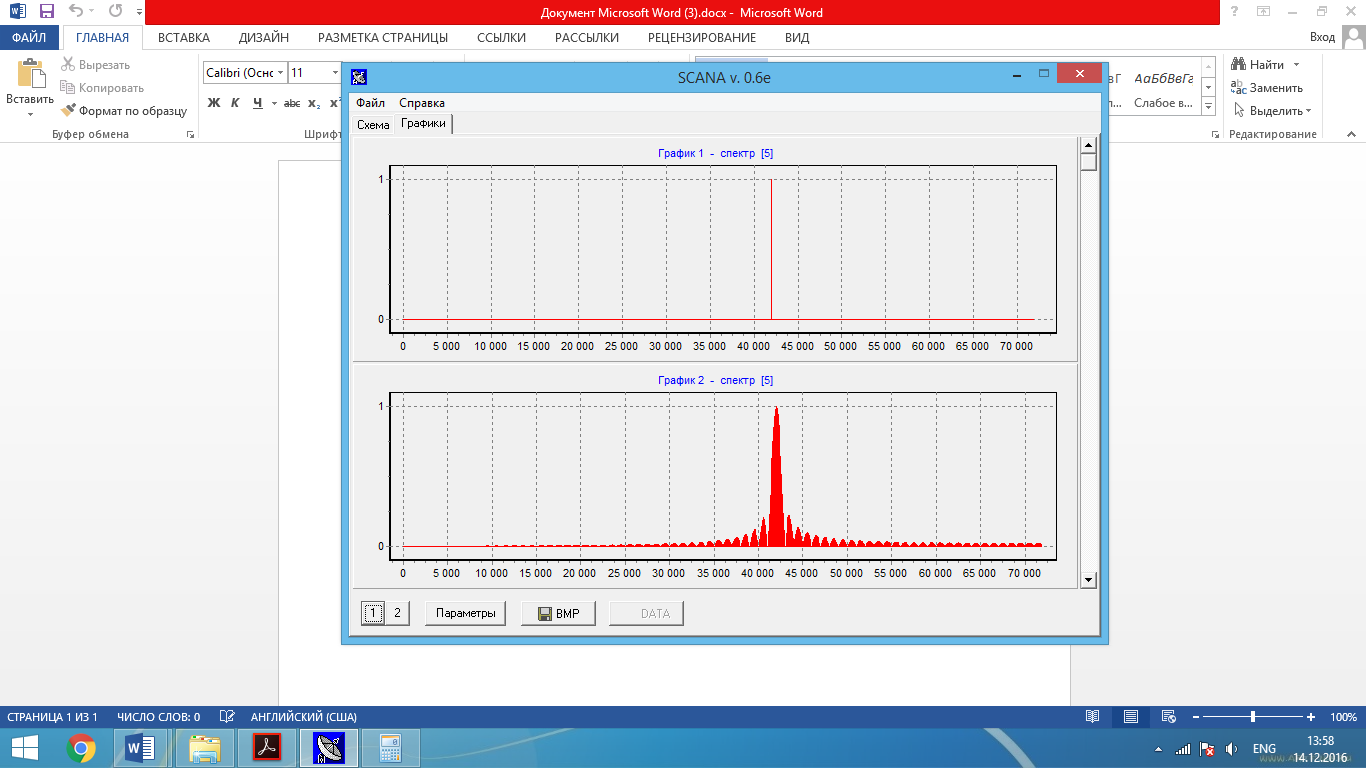
Рис. 1 – Объединенные попарно амплитудные характеристики (прямоугольная ВФ, ширина окна графиков – 144, число точек ДПФ 144 и 1440 соответственно)


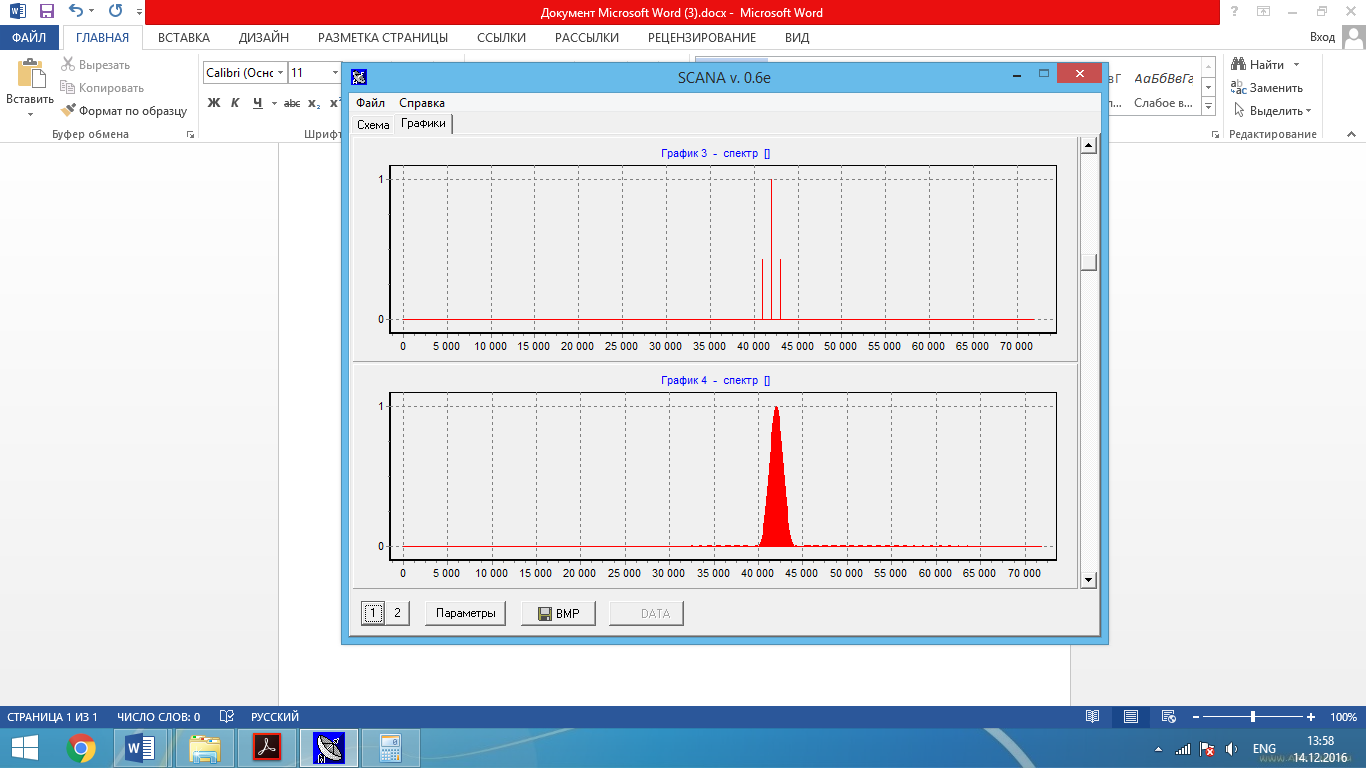
Рис. 2 – Объединенные попарно амплитудные характеристики (ВФ Хэмминга, ширина окна графиков – 144, число точек ДПФ 144 и 1440 соответственно)
Значение фазы частотных выборок сигнала (по графикам 1,3) – 60º соответственно.

Изменим значение частоты тестового сигнала, установив его равным 42,5 кГц.



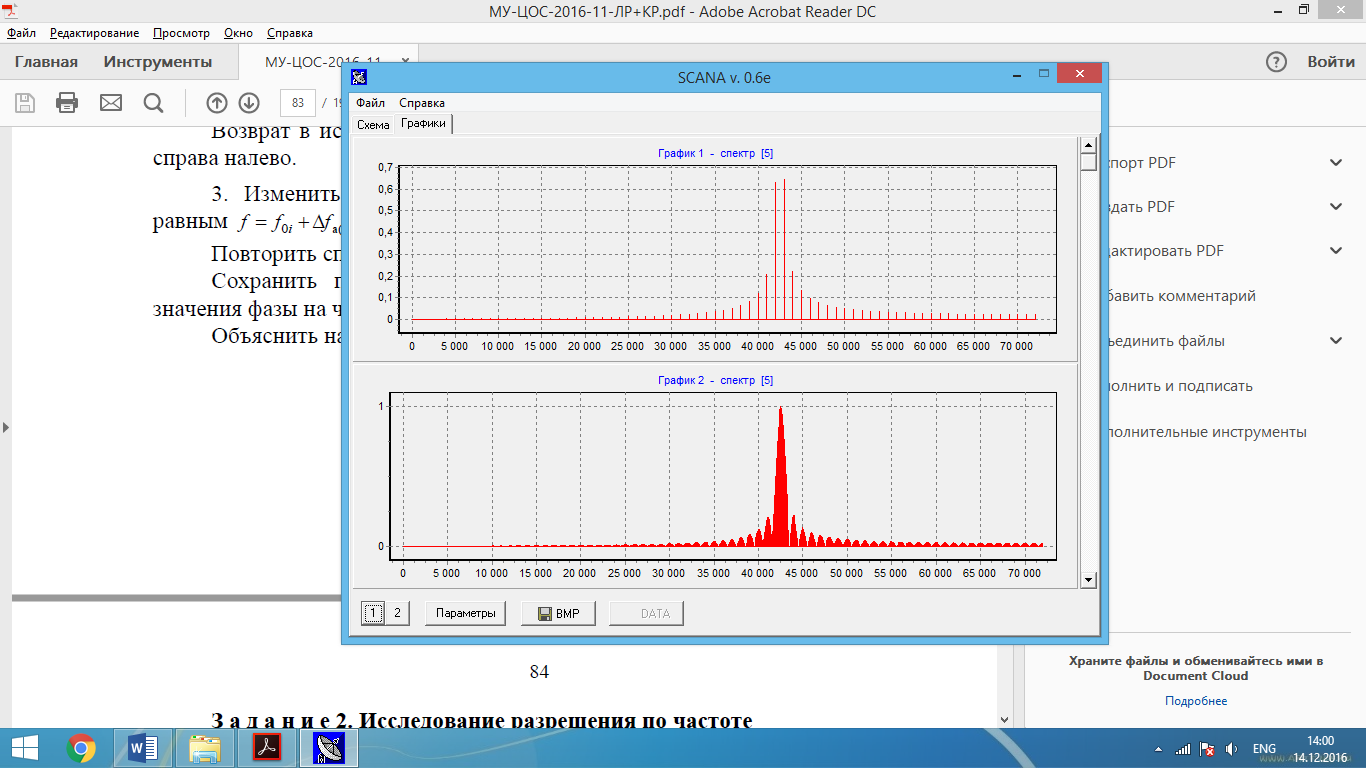
Рис. 3 – Объединенные попарно амплитудные характеристики (прямоугольная ВФ, ширина окна графиков – 144, число точек ДПФ 144 и 1440 соответственно)



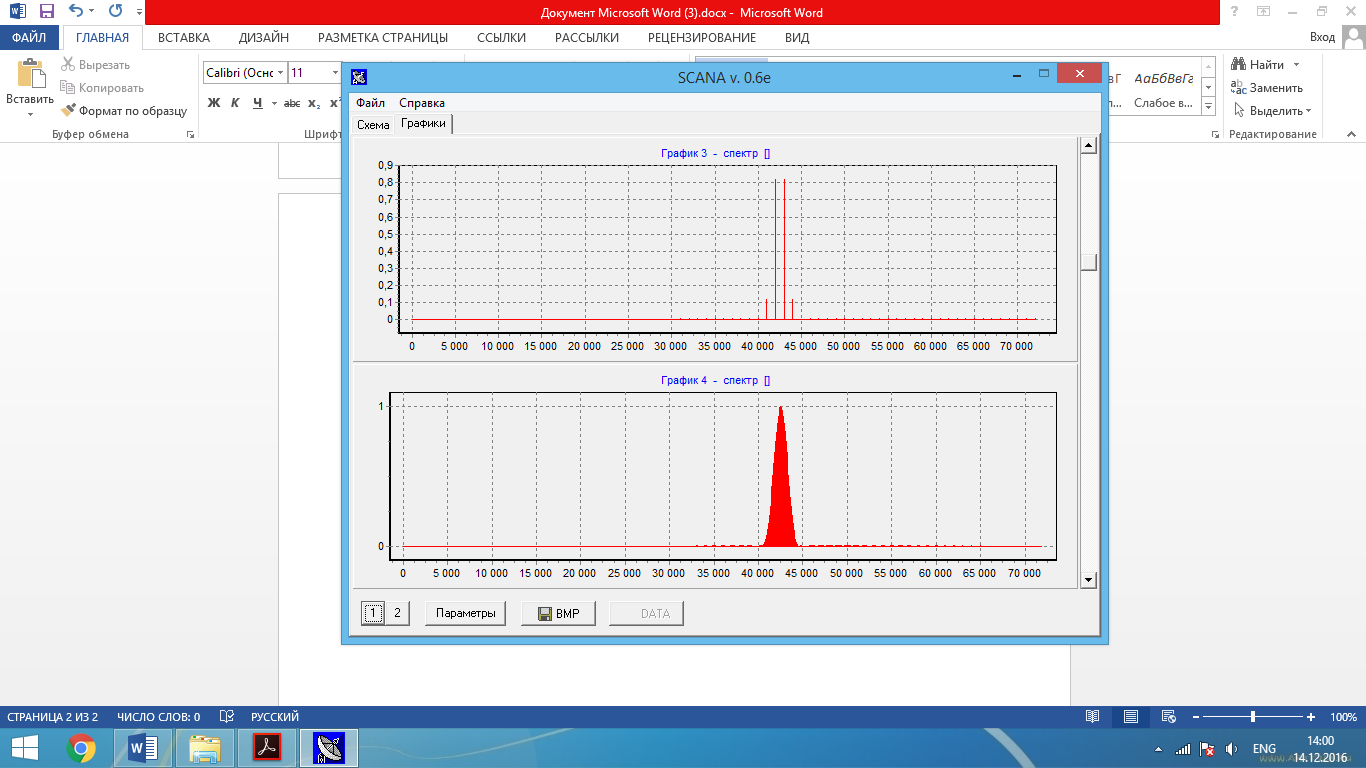
Рис. 4 – Объединенные попарно амплитудные характеристики (ВФ Хэмминга, ширина окна графиков – 144, число точек ДПФ 144 и 1440 соответственно)
Значение фазы частотных выборок сигнала (по графикам 1,3) – 60º соответственно.
Задание 2. Исследование разрешения по частоте анализатора спектра на основе ДПФ.
С помощью генератора многочастотного сигнала синтезировать тестовый трехчастотный сигнал с некратными частотами и начальными фазами гармоник f₀ = 42 кГц, φ₀=60º, f₁ = 40,8 кГц, φ₁=30º, f₂ = 43,2 кГц, φ₂=90º одинаковой амплитудой 1 В, которые нужно разрешить раздельно.



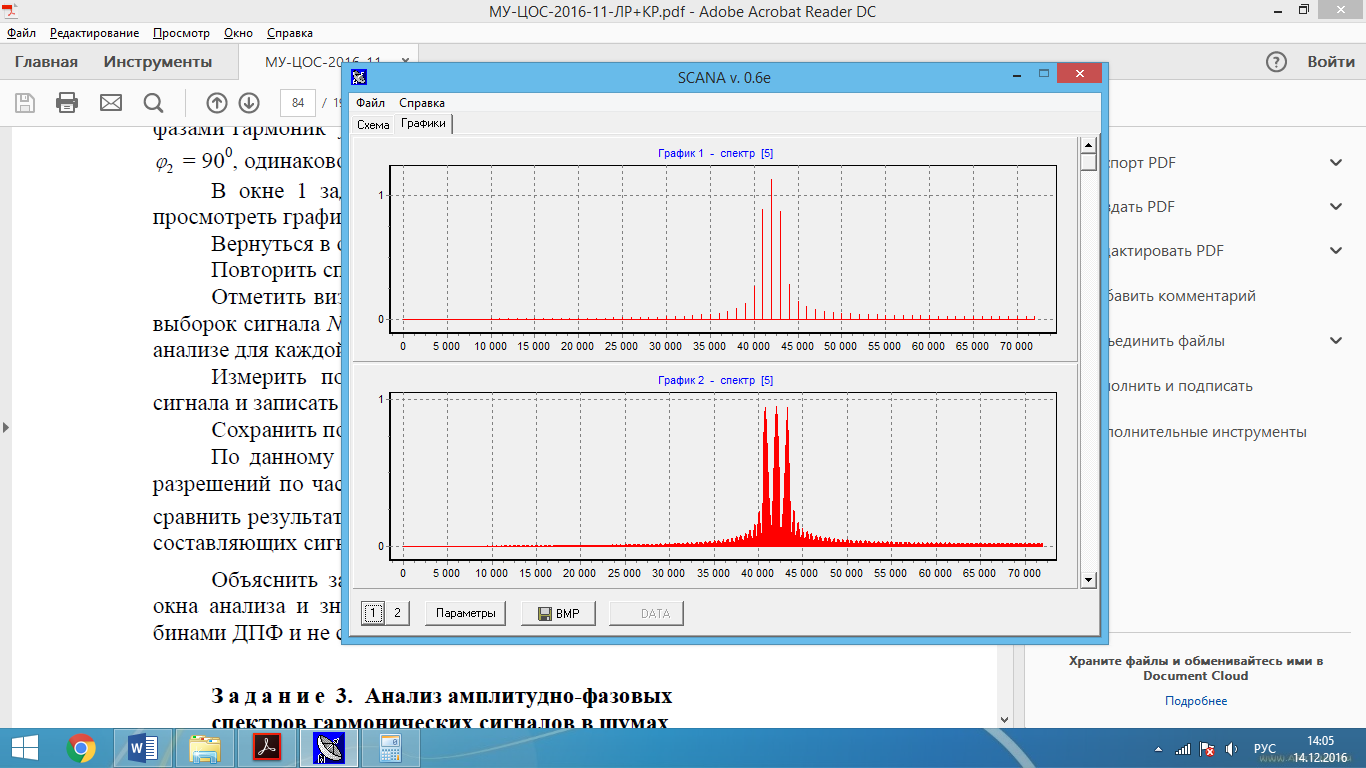
Рис. 5 – Объединенные попарно амплитудные характеристики (прямоугольная ВФ, ширина окна графика 1 – 144, ширина окна графика 2 – 288, число точек ДПФ– 1440)



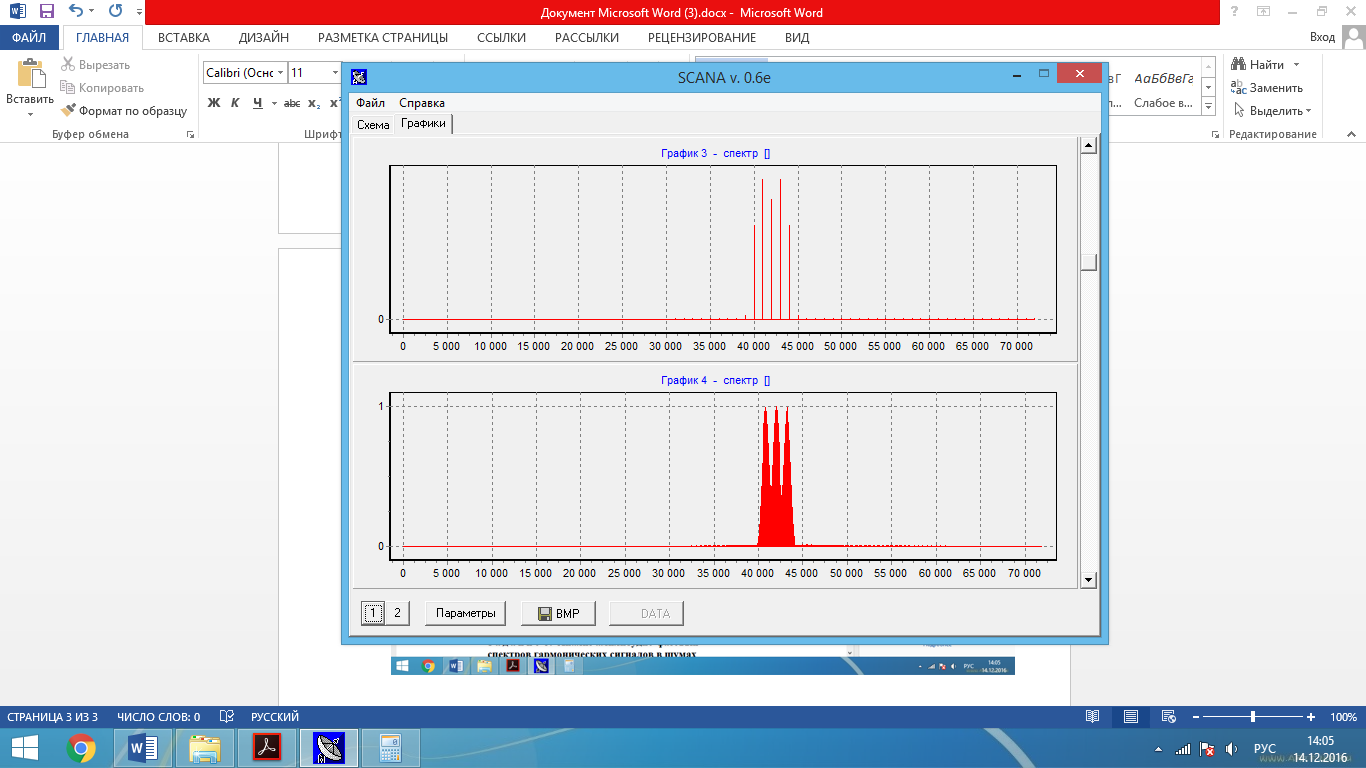
Рис. 6 – Объединенные попарно амплитудные характеристики (ВФ Хэмминга, ширина окна графика 3 – 144, ширина окна графика 4 – 288, число точек ДПФ– 1440)
Табл.1 – График 2 (значения амплитуд):

Амплитуда	0,945	0,950	0,943
Частота, кГц	40,8	42	43,2

---

Табл.2 – График 4 (значения амплитуд):

Амплитуда	0,996	1	0,996
Частота, кГц	40,8	42	43,2

По данному заданию рассчитал теоретические значения разрешений по частоте

Окно 1



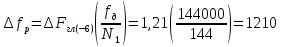
Окно 2



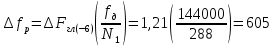
Окно 3



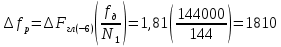
Окно 4



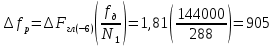
Задание 3. Анализ амплитудно-фазовых спектров гармонических сигналов в шумах
Установить параметры генератора многочастотного сигнала, соответствующие одночастотному гармоническому сигналу с частотой 42 кГц, амплитудой 1 В, начальной фазой 60º и подключить к сумматору с помощью ключа 3 источник шума с СКЗ (с сигма шума), равным 1 В.



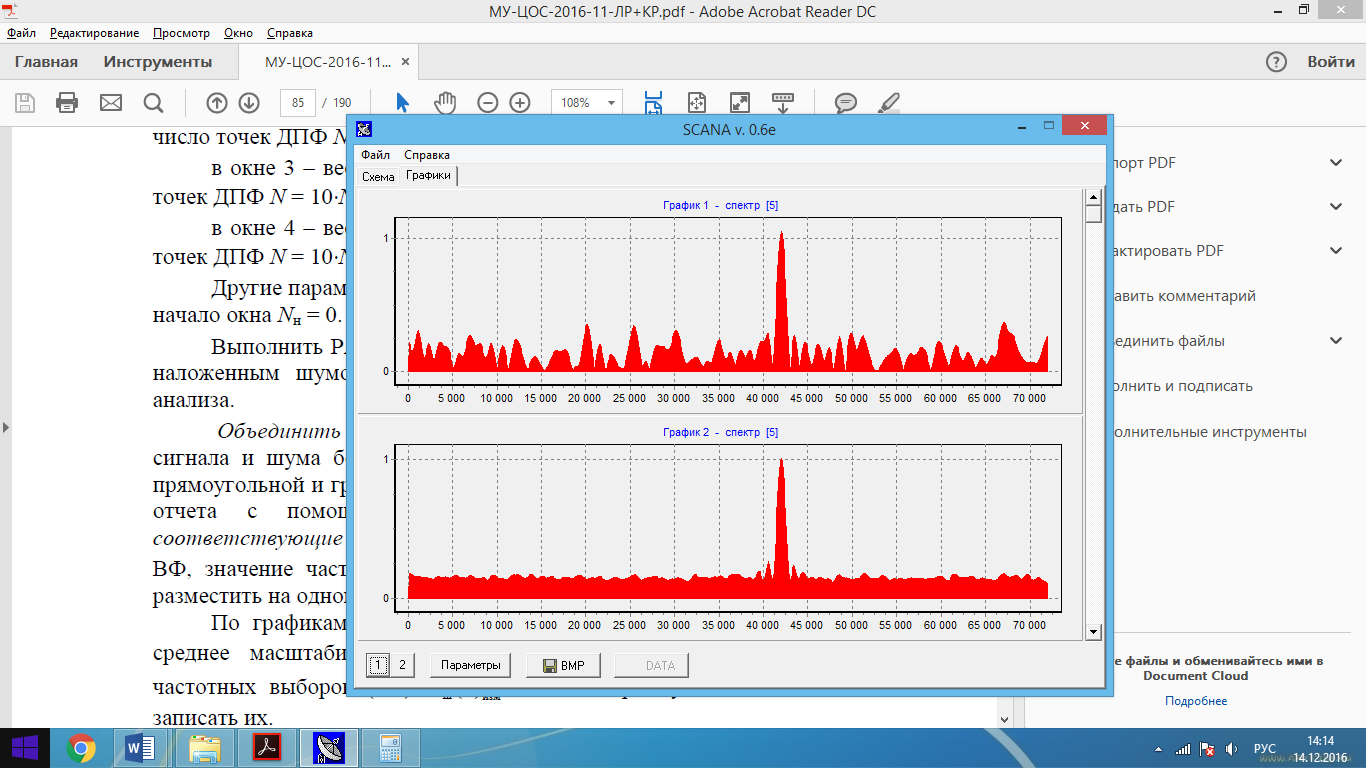
Рис. 7 – Объединенные попарно амплитудные характеристики (прямоугольная ВФ, ширина окна графика 1 – 144, ширина окна графика 2 – 144, число точек ДПФ– 1440, число усредняемых окон 1– для графика 1 и 32 – для графика 2)




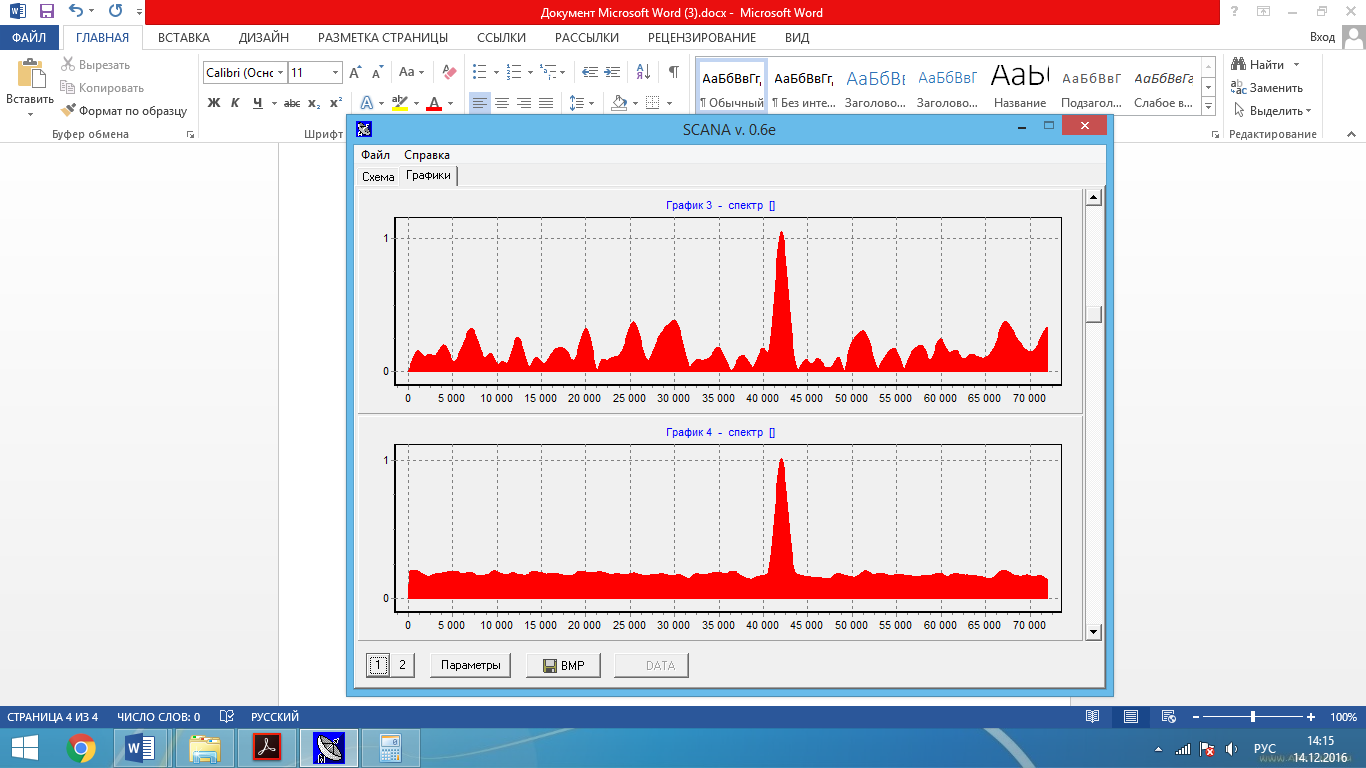
Рис. 8 – Объединенные попарно амплитудные характеристики (ВФ Хэмминга, ширина окна графика 3 – 144, ширина окна графика 4 – 144, число точек ДПФ– 1440, число усредняемых окон 1– для графика 3 и 32 – для графика 4)
По графикам спектров амплитуд при L=32 (окна 2,4) измерим приближенно среднее масштабированное значение сигнальной и шумовых частотных выборок для ВФ прямоугольной и Хэмминга. Также проведем «Рандомизацию».

	Сигнальная выборка	Шумовая выборка
Окно 2	1.007	0.16
Окно 4	1.016	0.18

---

По заданию 3 выполнил расчеты:

Окно 2







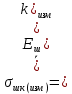
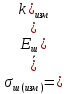
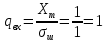
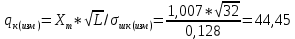
Окно 4









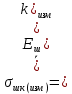
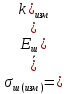
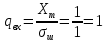
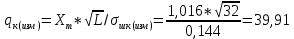
Рис. 9 – Структурная схема анализатора спектра на основе ДПФ представленная

его базовыми элементами

ВЫВОД
В ходе работы закрепил освоение методов и программных средств спектрально-корреляционного анализа сигналов, основанного на дискретном (быстром) преобразовании Фурье (ДПФ-БПФ).

ОТВЕТЫ НА ВОПРОСЫ

1. Какова базовая структура анализатора спектра на основе ДПФ и его математическое обеспечение?





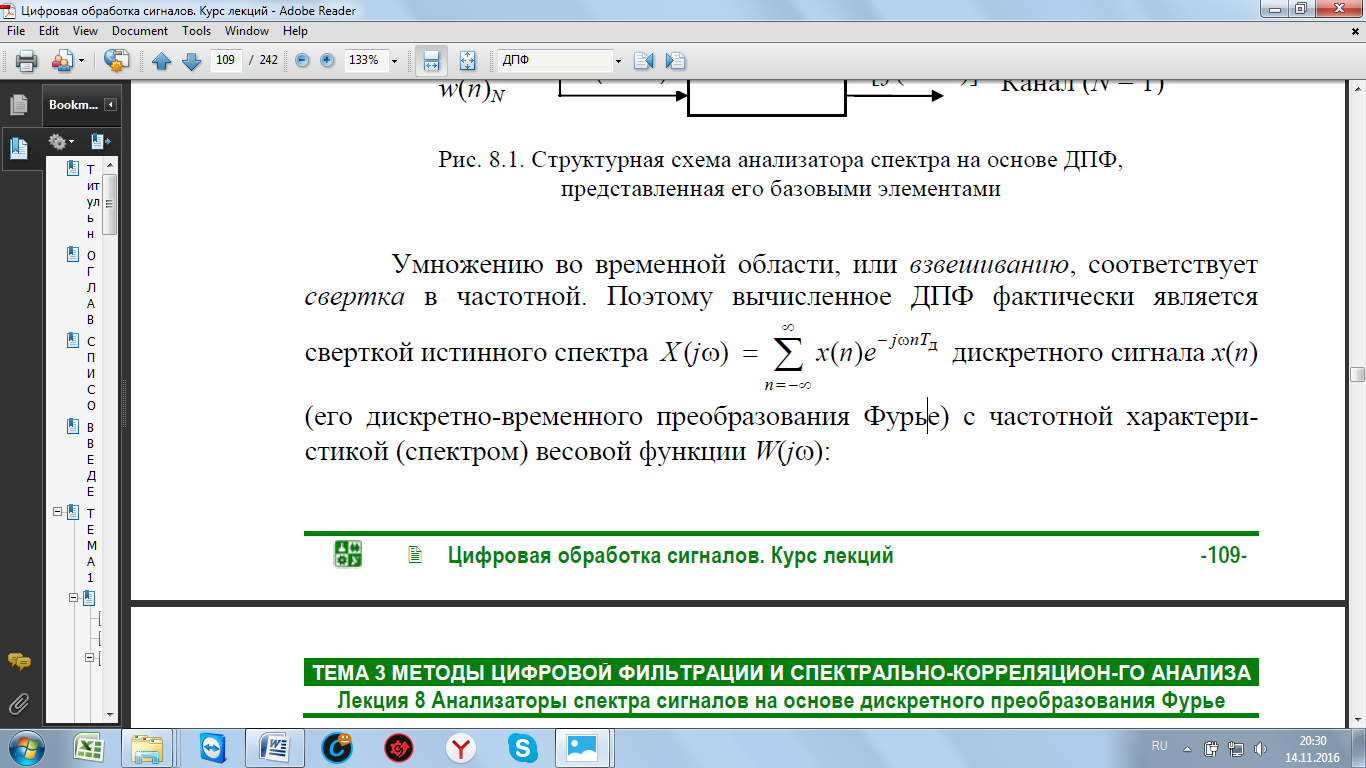
2. Как обеспечивается однозначное разрешение известных частотных составляющих в гармоническом анализе на основе ДПФ?

Однозначное разрешение комплексного гармонического сигнала анализатором спектра с прямоугольной весовой функцией имеет место только

на частотах ω_х = ω_k, совпадающих с частотами анализа ДПФ, когда на интервале анализа укладывается целое число периодов сигнала: Tа =(N–1)Tд = kT
3. Как определяется СПМ дискретного случайного сигнала и ее статистическая оценка?

Спектральную плотность мощности (СПМ) случайного сигнала в

соответствии с теоремой Винера−Хинчина определяют преобразованием Фурье АКФ (последовательности rxx(m)) для значений частоты f, заключенных в основной полосе частот (0 ± fд/2):



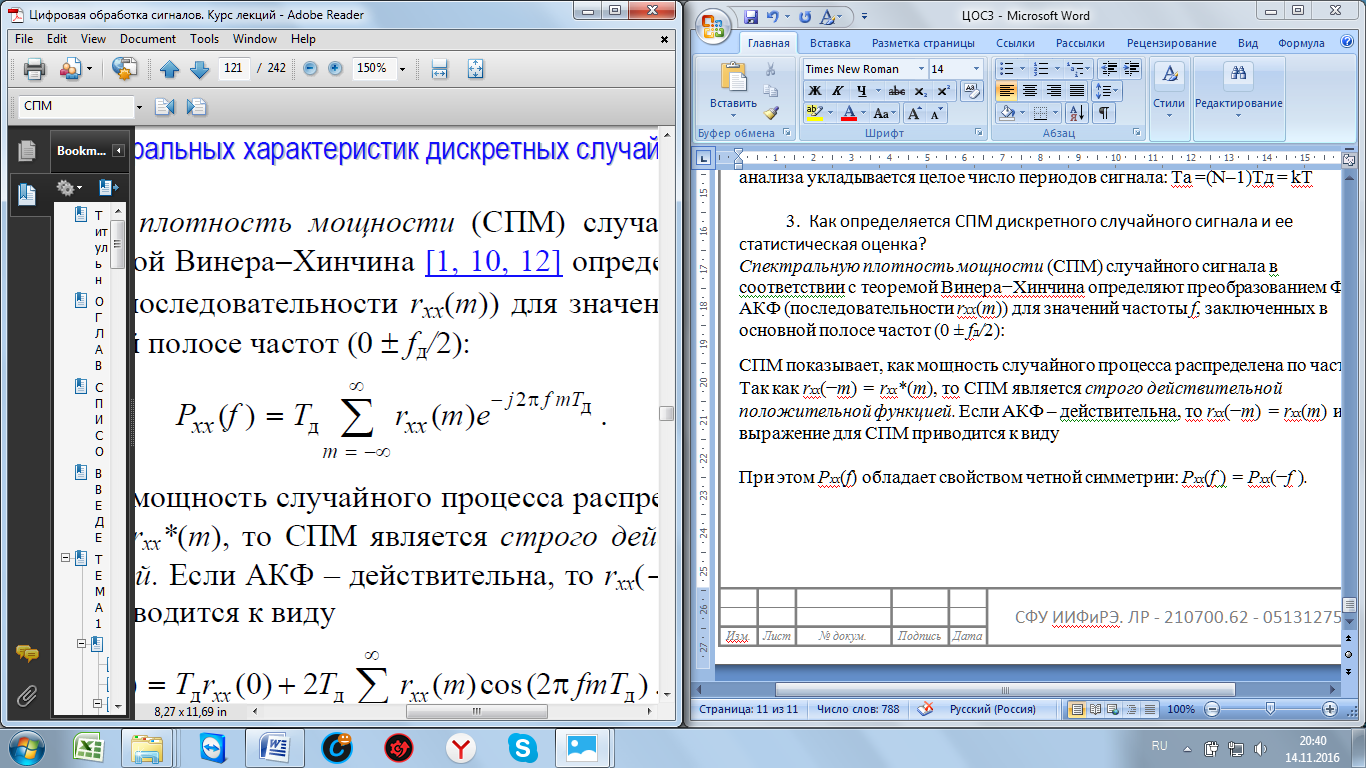
СПМ показывает, как мощность случайного процесса распределена по частоте. Так как rxx(−m) = rxx*(m), то СПМ является строго действительной положительной функцией.

---

Если АКФ – действительна, то rxx(−m) = rxx(m) и выражение для СПМ приводится к виду



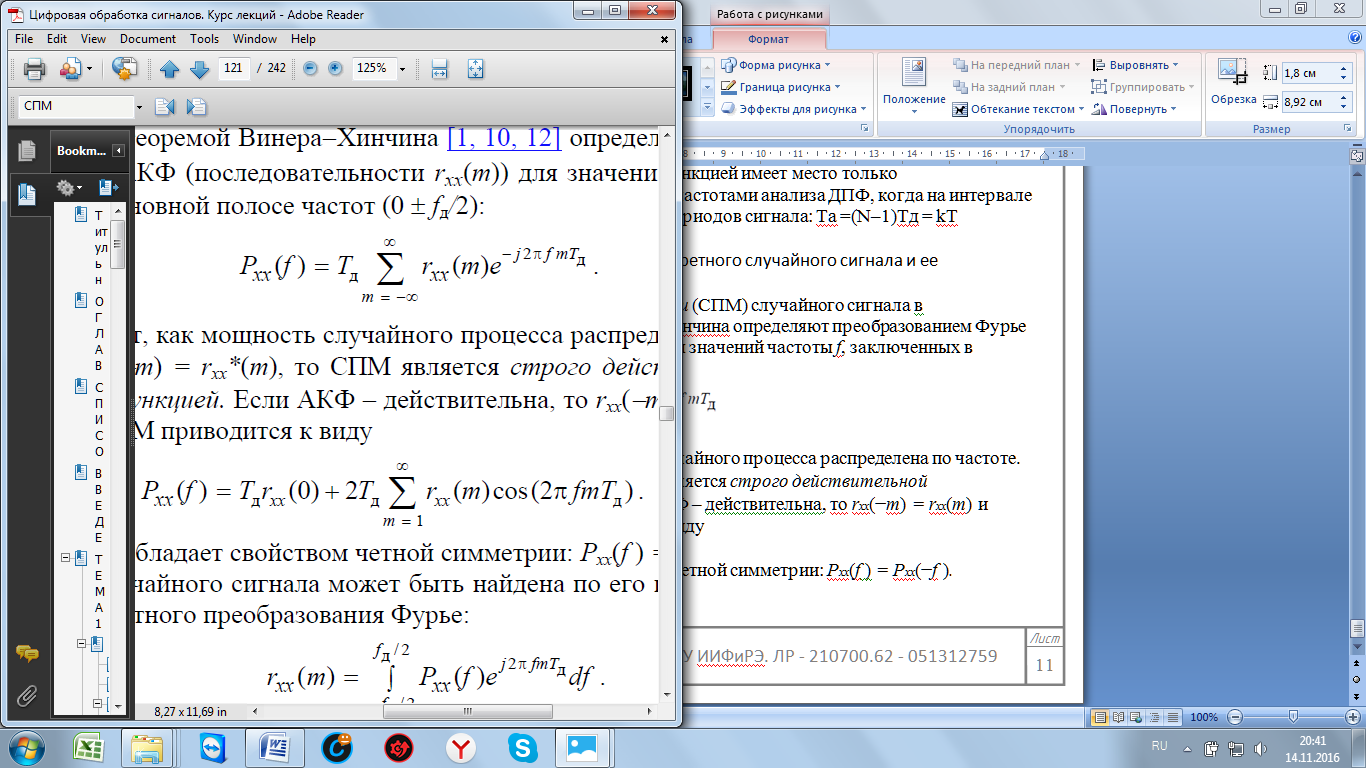
При этом Pxx(f) обладает свойством четной симметрии: Pxx(f ) = Pxx(−f ).

4. Как вычисляется ВКФ с помощью ДПФ?

Взаимная корреляционная функция (ВКФ) r_xy(m) = E{x(n +m)y*(n)} –

математическое ожидание произведения задержанной копии x(n + m) случайного сигнала x(n) и комплексно-сопряженного сигнала y*(n).

---

Смотрите также файлы

• Теория эффективного лидерства и командный менеджмент рабочая тетрадь.docx

• Ответ трудовое законодательство той страны, где Потапова заключила трудовой договор. Задача 4.docx

• Способы группировки информации Курышев Алексей 2307 Тест.docx

• Основные положения теории лидерства Ицхака Адизеса.pptx

• К числу письменных источников по Истории государства и права зарубежных стран относятся такие, как .docx