ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.10.2024
Просмотров: 2
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ» |
| Кафедра экономики и управления Форма обучения: заочная |
ВЫПОЛНЕНИЕ
ПРАКТИЧЕСКИХ ЗАДАНИЙ
ПО ДИСЦИПЛИНЕ
«Математические методы в психологии»
Группа Го21П171в
Студент
И.В.Богданович
МОСКВА 2023
Задания к практической работе 1.
Определение числовых характеристик.
Задание 1.
| xi | 30-80 | 80-130 | 130-180 | 180-230 | 230-280 | 280-330 |
| ni | 15 | 13 | 7 | 5 | 3 | 2 |
Проведено выборочное обследование частных психологических кабинетов города. Имеются следующие данные о величине посещаемости для 50 кабинетов города (xi – количество клиентов в месяц, млн. руб.; ni – число кабинетов).
Найти:
а) среднее X, среднеквадратичное отклонение S и коэффициент V;
б) построить гистограмму и полигон частот.
Решение:
Перейдем к простому вариационному ряду, выбирая в качестве значений середины интервалов. Получим:
| xi | 55 | 105 | 155 | 205 | 255 | 305 |
| ni | 15 | 13 | 7 | 5 | 3 | 2 |
Найдем необходимые числовые характеристики на основе последовательных расчетов:
| xi | 55 | 105 | 155 | 205 | 255 | 305 | Σ |
| ni | 15 | 13 | 7 | 5 | 3 | 2 | 45 |
| xi ni | 825 | 1 365 | 1 085 | 1 025 | 765 | 610 | 5 675 |
| (xi-X)2*ni | 75 615 | 5 733 | 5 887 | 31 205 | 49 923 | 64 082 | 232 445 |
Среднее: X = (1/n) * Σ (xi ni) = (1/45) * 5 675 = 126
Дисперсия: S2 = (1/n) * Σ ((xi-X)2*ni) = (1/50) * 232 445 = 4649
Среднеквадратичное отклонение: S = √S2 ≈ 68,184
Коэффициент вариации: V=(S/X) * 100% = (68,184/126) * 100% = 54, 11%
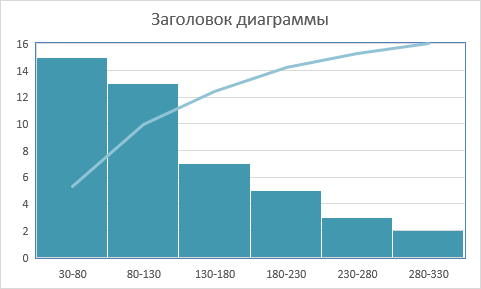
Задание 2.
Из генеральной совокупности извлечена выборка объема n. Найти среднее значение, дисперсию, среднее квадратическое отклонение, исправленную дисперсию, коэффициент вариации, моду и медиану.
| xi | 9,5 | 10 | 10,5 | 11 | 11,5 | 12 | 12,5 |
| ni | 3 | 15 | 30 | 15 | 5 | 4 | 2 |
Решение:
Составим таблицу значений.
| xi | 9,5 | 10 | 10,5 | 11 | 11,5 | 12 | 12,5 | Σ |
| ni | 3 | 15 | 30 | 15 | 5 | 4 | 2 | 74 |
| xi ni | 28,5 | 150 | 315 | 165 | 57,5 | 48 | 25 | 789 |
| (xi-X)2*ni | 38,3496 | 6,534 | 0,768 | 1,734 | 3,528 | 7,1824 | 6,7712 | 57, 68 |
Среднее значение: X = (1/n) * Σ (xi ni) = (1/74) * 789 = 10,66
Дисперсия D = (1/n) * Σ ((xi-X)2 * ni) = (1/74) * 57,68 = 0,78
Исправленная дисперсия S2 = n/(n-1) * D = 74/(74-1) * 0,78 ≈ 0,790
Среднеквадратичное отклонение σ = √D = 0,759
Исправленное среднеквадратичное отклонение S = 0,889
Коэффициент вариации V = σ/X * 100% = 0,759/10,66*100% = 7,12%
Мода – величина с наибольшей частотой Мо = 10,5
Медиана - величина, находящаяся в середине ряда Ме = 11
Задания к практической работе 2.
Статистическая обработка данных.
Задание 1.
У 24 девушек – студентов физического и психологического факультетов был измерен уровень вербального интеллекта по методике Векслера.
Можно ли утверждать, что одна из групп превосходит другую по уровню вербального интеллекта?
Физики: 123, 134, 126, 131, 134, 132, 126, 132, 127, 127, 136, 133, 136, 135,
Психологи: 123, 125, 132, 120, 127, 126, 120, 126, 120, 119,
Решение:
Используем критерий Q Розенбаума. Упорядочим значения в обеих выборках, а затем сформулируем гипотезы:
H0: Студенты-физики не превосходят студентов-психологов по уровню вербального интеллекта.
H1: Студенты-физики превосходят студентов-психологов по уровню вербального интеллекта.
| Физики | Психологи |
| 136 | |
| 136 | |
| 135 | |
| 134 | |
| 134 | |
| 133 | |
| 132 | 132 |
| 132 | |
| 131 | |
| 127 | 127 |
| 127 | |
| 126 | 126 |
| 126 | 126 |
| | 125 |
| 123 | 123 |
| S2 | 120 |
| 120 | |
| 120 | |
| 119 |
Определяем количество значений первого ряда, которые больше максимального значения второго ряда: S1=0.
Теперь определяем количество значений второго ряда, которые меньше минимального значения первого ряда: S2=4.
Вычисляем Qэмп по формуле: Qэмп = S1+S2 = 0+4 = 4.
Критические значения Q для n1=14, n2=10 не могут быть определены, так как одна из выборок (общее количество значений второго ряда) содержит в себе менее 11 наблюдений.
Задание 3.
Психолог просит супругов проранжировать девять личностных черт, имеющих определяющее значение для семейного благополучия. Задача заключается в том, чтобы определить, в какой степени совпадают оценки супругов по отношению к ранжируемым качествам. Заполните таблицу и, посчитав коэффициент ранговой корреляции Спирмена, ответьте на поставленный вопрос.
| Черты личности | № | Муж | Жена |
| Ответственность | 1 | | |
| Общительность | 2 | | |
| Сдержанность | 3 | | |
| Выносливость | 4 | | |
| Жизнерадостность | 5 | | |
| Терпеливость | 6 | | |
| Решительность | 7 | | |
| Оптимизм | 8 | | |
| Надежность | 9 | | |
Решение:
Заполняем таблицу. Далее, рассчитываем коэффициент ранговой корреляции Спирмена и составляем расчетную таблицу.
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Σ |
| Ранг X, dx | 2 | 3 | 4 | 6 | 5 | 1 | 7 | 8 | 9 | 45 |
| Ранг X, dy | 2 | 5 | 1 | 7 | 6 | 3 | 4 | 9 | 8 | 45 |
| (dx–dy )2 | 0 | 4 | 9 | 1 | 1 | 4 | 9 | 1 | 1 | 30 |
Вычисляем коэффициент ранговой корреляции Спирмена.
P = 1 – 6 * ((d2)/(n3 - n)) = 1 – 6 * ((302) / (93 - 9)) = - 6,5
Ответ: согласованности между мнениями супругов нет.
