ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.10.2024
Просмотров: 3
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3.3.1 БАНК «ПРОСТОР»
Банк «Простор» имеет проблемы с планированием работы персонала в связи с резким изменением потока клиентов в течение дня. Во время наибольшего притока клиентов их количество в единицу времени бывает обычно в 5-6 раз больше, чем в спокойные часы перед закрытием. С помощью теории очередей было рассчитано необходимое для качественного обслуживания количество персонала в каждом часовом промежутке с 9 до 19 ч.
Результаты представлены в таблице.
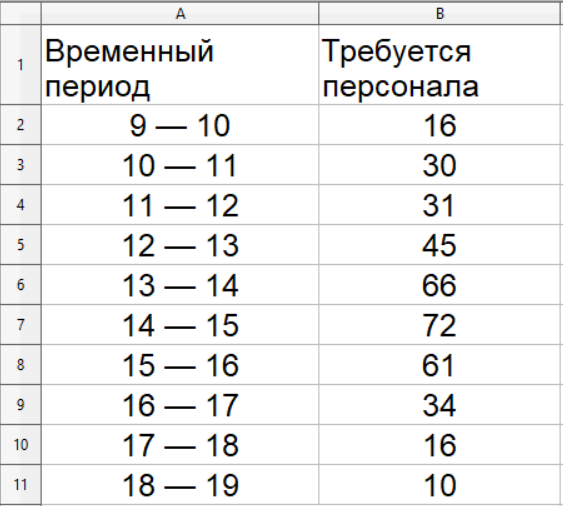
Служащие, занятые в банке полный день, работают либо с 9 до 17 ч с перерывом на обед с 12 до 13 ч, либо с 11 до 19 ч с перерывом на обед с 14 до 15 ч. Их часовая ставка составляет 8 долл.
Возможно также использование служащих, занятых неполный день (4 рабочих часа подряд). Их часовая ставка зависит от временного промежутка, на который их нанимают (см. таблицу).

a. Рассчитайте оптимальное количество служащих на полный день и с неполной занятостью и составьте расписание их работы. Какова общая заработная плата всех служащих в день?
b. Результаты расчета вызвали недовольство руководства, и управляющий потребовал, чтобы в любое время в банке работало не менее 4 служащих, занятых полный день. Составьте новое расписание. Какова теперь общая заработная плата всех служащих в день?
c. Новые результаты также показались руководству неудовлетворительными, так как общее число служащих превысило 100 человек, что должно привести к переходу организации в другую налоговую группу и общему увеличению различных налоговых выплат. Необходимо сократить количество персонала, работающего с клиентами, до 94 человек. Составьте новое расписание. Какова теперь общая заработная плата всех служащих в день?
Решение задачи
Из текста задачи следует, что целевой функцией должна являться заработная плата служащих, скажем, в расчете на день, так как по условиям задачи дни не отличаются друг от друга и месячный фонд заработной платы получится простым умножением дневной оплаты на число рабочих дней. Оптимальное количество служащих в таком случае будет соответствовать минимуму заработной платы при соблюдении всех ограничений задачи.
Суммарная заработная плата, в свою очередь, зависит от количества служащих, занятых полный день, и количества служащих, занятых частично и работающих во временных интервалах, перечисленных в строке “Время найма”. Поэтому в качестве переменных решения разумно выбрать 9 переменных: Х1 и Х2 – количество служащих полного дня, работающих с 9 до 17 ч и с 11 до 19 ч соответственно; Х3, Х4, ..., Х9 –количество служащих неполного дня, работающих во временных интервалах 9 - 13 ч, 10 -14 ч, 15 - 19 ч соответственно.
Очевидно, что если бы значения переменных были нам известны, то суммарная заработная плата определилась бы из целевой функции следующего вида:
С = Х1*8 + X2*8 + X3*6 + X4*7 + X5*9 + X6*10 + X7*8 + X8*6 + X9*6 (долл.)
Так как банк задаёт необходимые количества служащих для каждого рабочего часа отдельно, то мы должны уметь рассчитывать наличие служащих в любом часовом интервале, используя значения переменных. Для того чтобы это сделать, организуем данные на листе OpenOffice Calc так, как показано в таблице (рис. 1).

Рис. 1
В ячейках С15:К15 этой таблицы содержатся переменные задачи Х1, ..., Х9, в ячейке L15– целевая функция. Ячейки в прямоугольнике С2:К11 содержат двоичные числа 0 либо 1 (пустая ячейка полагается при расчетах в MS Excel, содержащей нулевое значение). Единицы означают, что соответствующий служащий работает в данном часовом промежутке (указанном в крайнем столбце слева), пробел или 0 – что не работает. Например, то, что I в ячейке F6 записана 1, означает, что служащий, работающий во времен- I ном интервале с 10 до 14 ч, показанном в заголовке столбца F, работает в I промежутке с 13 до 14 ч (заголовок строки 6). Нули в ячейках С5 и D7 проставлены, чтобы подчеркнуть расположение обеденных перерывов у служащих, занятых полный день.
При такой организации данных функция
=SUMPRODUCT(_C2:K2_;_$C$15:$K$15_)'>=SUMPRODUCT(C2:K2;$C$15:$K$15)
перемножающая строку переменных на строку способных работать в часовом промежутке с 9 до 10 ч, позволяет узнать, сколько человек будет работать в это время при заданных значениях переменных X,, Х2, ..., АТ9. В столбце L2:L11 подсчитываются количества служащих для каждого часового промежутка.
В целевой ячейке L15 функция =SUMPRODUCT(C15:K15;
C13:K13) вычисляет суммарную заработную плату всех служащих. Для этого в строке 13 предварительно подсчитаны дневные заработки для каждой категории служащих.
Теперь у нас имеются все данные и функции, необходимые для работы надстройки Поиск решения. Вызываем Сервис/Решатель, в качестве целевой ячейки указываем L15. Целью оптимизации полагаем поиск минимального значения. В окне Изменяя ячейки указываем переменные C15:K15. Далее нажимаем кнопку Параметры, чтобы отметить OpenOffice линейный решатель и поставить галочку Принять переменные как неотрицательные.
После этого остаётся только задать условия, которым должно удовлетворять решение. В нашем случае основное условие только одно – фактические количества служащих в каждом часовом промежутке должны быть не меньше, чем заданные в условиях задачи. В области Ограничительные условия указываем, что числа в ячейках L2:L11 должны быть больше или равны числам в ячейках B2:B11. Кроме того, так как количество служащих невелико, добавляем условие, чтобы переменные были целые. Теперь можно запустить процедуру поиска решения (Решить).
Если все введено правильно, должен получиться следующий результат (рис. 2).
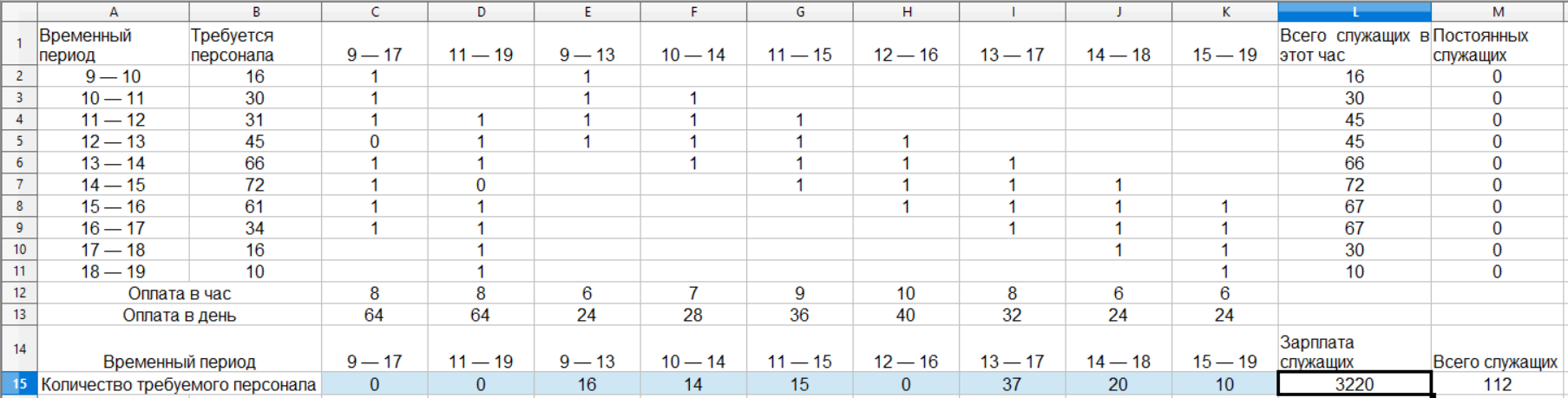
Рис. 2
Таким образом, мы получили ответ на вопрос a. Общая заработная плата составит 3220 долл. в день. При этом будут наняты только служащие, занятые неполный день: работающие с 9 до 13 ч – 16 человек, с 10 до 14 ч – 14, с 11 до 15 ч – 15, с 13 до 17 ч – 37, с 14 до 18 ч – 20 и с 15 до 19 ч – 10 человек. При этом в четырёхчасовых промежутках из 10 общее количество служащих превысит минимально возможное количество: в промежутке 11 – служащих превысит минимально возможное количество: в промежутке 11 – 12 ч – 45 человек вместо 31, и в промежутках 15 – 16, 16 – 17 и 17 – 18 ч – 67, 67 и 30 служащих вместо 61, 34 и 16 соответственно. Общее число служащих, работающих в банке, достигает 112 человек.
b. Анализ полученного раннее решения показал, что оптимальным является наем только служащих неполного дня. Если такое решение неприемлемо, следует модифицировать задачу, задав соответствующее ограничение. В данном случае необходимо иметь не менее 4 служащих, занятых полный день. Для подсчёта служащих, занятых полный день, работающих в заданном часовом интервале, используем функцию вида
=SUMPRODUCT(C2:D2;$C$15:$D$15), аналогичную той, что подсчитывает полное число сотрудников, работающих в заданном часовом интервале, но теперь учитывающее только две переменные Х1 и Х2. Нам нужно ввести дополнительный столбец М2:М11, в котором будут подсчитываться количества служащих полного дня в каждом из десяти часовых интервалов. Соответственно и в задание для Поиска решения введём добавочное условие – М2:М11 >= 4.
После запуска Поиска решения на выполнение получим следующий результат
(рис. 3):
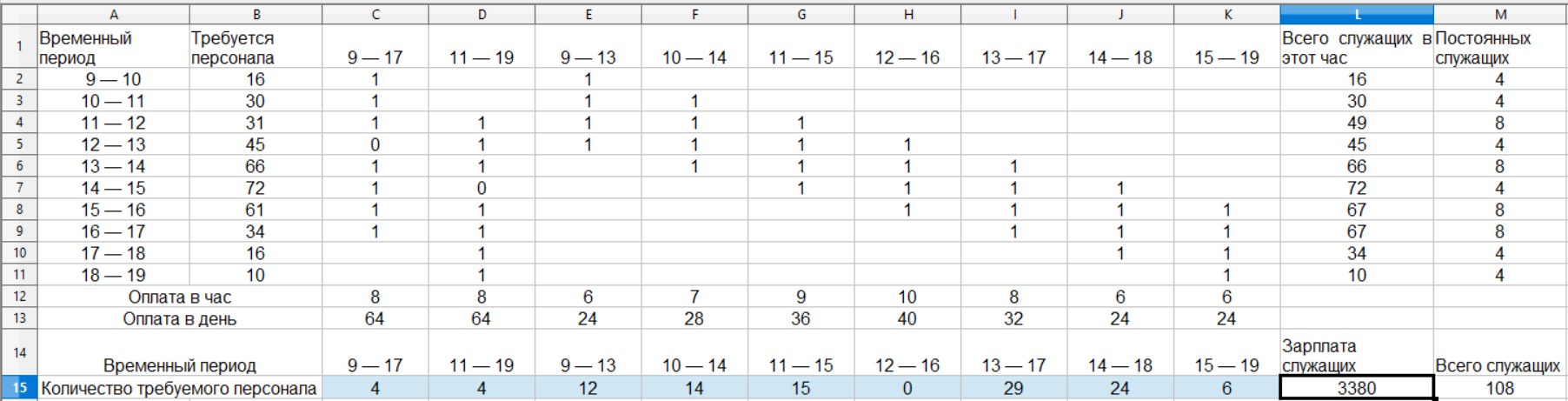
Рис. 3
Общая заработная плата увеличилась до 3380 долл. (больше на 160 долл.), нанято наименьшее возможное число постоянных служащих – 8 человек.
Общее число служащих уменьшилось до 108 человек.
с. Новое ограничение, связанное с общим количеством служащих, учесть очень легко. Добавим в ячейку М15, например, функцию =SUM(C15:K15), вычисляющую общее количество служащих, суммируя все переменные. Вызываем Поиск решения и добавляем ограничение М15 <=94. Снова запускаем Поиск решения на вычисление, получаем ответ, что решение найдено!
Это новое решение приведено в таблице ниже (рис. 4):
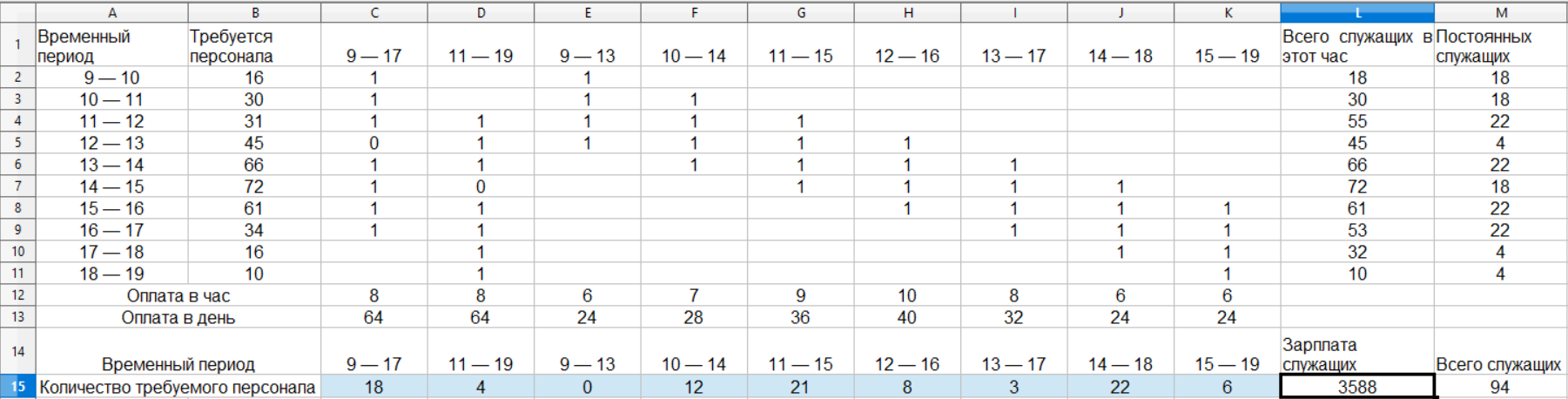
Рис. 4
При учете всех требований общий дневной фонд зарплаты вырастет до 3588 долл., что на 208 дол. больше, чем при найме 108 служащих, и на 368 долл. больше, чем при найме 112 служащих.
