ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.10.2024
Просмотров: 4
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема 7. Логические операции. Построение таблиц истинности (Лекция)
Результат обучения: Переводить целые числа из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную и обратно
Критерии оценки: Строит таблицы истинности для заданного логического выражения
Термины:
| Русский | Казахский | Английский |
| Дизъюнкция | Дизъюнкция | Disjuntion |
| Конъюнкция | Конъюнкция | Conjunction |
| Инверсия | Инверсия | Inversion |
| Таблица истинности | Ақиқат кестесі | Truth table |
Дополнительный материал:
-
Элементы алгебры логики Логические операции - https://youtu.be/jd6A4nrezxY -
Законы алгебры логики - https://youtu.be/ifSujVn_MZE -
Пример построения таблиц истинности - https://youtu.be/DW5v3r45RIA
Логика (от древнегреческого logos – слово, мысль) – совокупность правил, которым подчиняется процесс мышления.
Мышление – высшая форма познавательной деятельности человека. Чтобы человек правильно мыслил, он должен подчиняться определенным правилам и закономерностям

1. Первые учения о рассуждениях возникли в странах Древнего Востока (Индия, Китай).
2. Но в основе современной логики лежат учения, созданные древнегреческими мыслителями еще в VI-V вв. до н.э. Установившаяся в Греции демократическая жизнь потребовала развития искусства убеждения риторики, ораторского искусства. Появились учителя риторики – софисты, учившие не только доказывать истинные утверждения, но и искусно их опровергать.
3. Научную систему логики впервые разработал греческий ученый Аристотель (IV в. до н.э.), ученик Платона, воспитатель Александра Македонского. Он заложил основы формальной логики (силлогистики) – науки о законах и формах мышления.
4. Немецкий ученый Готфрид Вильгельм Лейбниц, английский математик Джордж Буль, немецкий математик Готлоб Фреге разработали
математическую логику (алгебру логики) – науку, изучающую математические методы решения логических задач и построения логических схем, которые лежат в основе работы любого компьютера.
Высказывание – повествовательное предложение, о котором можно сказать, истинно оно или ложно (вопросительные и повелительные предложения высказываниями не являются).
«Каждый ромб – параллелограмм» - истинно
«Каждый параллелограмм - ромб» - ложно
Составное (сложное) высказывание получается из простых с использованием союзов связок.
Логическая переменная – простое высказывание, значение которого равно 0, если оно ложно, или равно 1, если оно истинно. Может обозначаться буквами латинского алфавита.
Логическая функция - составное высказывание, значение которого также 0 или 1. Обычно обозначается латинской буквой F.
Таблица истинности – таблица, отображающая значения составного логического выражения при всех возможных значениях, входящих в него простых высказываний.
АЛГЕБРА ЛОГИКИ (БУЛЕВА АЛГЕБРА)
Алгебра логики впервые появилась в XIX веке в работах английского математика Джорджа Буля. Это был результат стремления к решению традиционных логических задач алгебраическими методами.
Разработана для того, чтобы можно было определять истинность или ложность составных высказываний, не вникая в их содержание.
А = «Два умножить на два равно четырем»
В = «Два умножить на два равно пяти»
А=1 (истина); В=0 (ложь)
В алгебре логики над высказываниями можно производить определенные логические операции, в результате которых появляются новые составные высказывания.
Каждой логической операции соответствует своя таблица истинности.
Базовые логические операции: И, ИЛИ, НЕ
ЛОГИЧЕСКИЕ ОПЕРАЦИИ
-
Логическое сложение
| Словесное обозначение | Знаковое обозначение |
| дизъюнкция ИЛИ OR | + , , |
Объединение двух простых утверждений A и B в одно составное утверждение с помощью союза ИЛИ называется логическим сложением, или дизъюнкцией, а результат операции – логической суммой.
Таблица истинности логического сложения
| A | B | F |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
-
Логическое умножение
| Словесное обозначение | Знаковое обозначение |
| конъюнкция И AND | * , , |
Соединение двух простых высказываний A и B в одно составное с помощью союза И называется логическим умножением, или конъюнкцией, а результат операции – логическим произведением.
Таблица истинности логического умножения
| A | B | F |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
-
Логическое отрицание
| Словесное обозначение | Знаковое обозначение |
| инверсия НЕ NOT | ¬, ¯ |
Присвоение союза НЕ простому утверждению A называется логическим отрицанием, или инверсией, в результате выполнения этой операции появляется новое утверждение.
Таблица истинности логического отрицания
| A | F |
| 0 | 1 |
| 1 | 0 |
-
Логическое умножение с отрицанием
| Словесное обозначение | Знаковое обозначение |
| Штрих Шеффера И-НЕ NAND | , |
Высказывание со штрихом Шеффера истинно тогда и только тогда, когда либо А ложно, либо В ложно , либо А и В ложны одновременно. Оно ложно и в nом случае, если истинны и А и В одновременно.
Таблица истинности логического умножения с отрицанием
| A | B | F |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
-
Логическое сложение с отрицанием
| Словесное обозначение | Знаковое обозначение |
| Стрелка Пирса ИЛИ-НЕ NOR | |
Это сложное высказывание, которое означает "Ни А, ни В". Значение ИСТИНО тогда и только тогда когда выражения ЛОЖНЫ
Таблица истинности логического сложения с отрицанием
| A | B | F |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
-
Логическое следование
| Словесное обозначение | Знаковое обозначение |
| Импликация ЕСЛИ…, ТО… IMPLY | → |
Это сложное высказывание, которое означает "Ни А, ни В". Является ЛОЖНЫМ тогда когда условие ИСТИНО, а следствие ЛОЖНО.
Таблица истинности логического сложения с отрицанием
| A | B | F |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
-
Логическая равнозначность
| Словесное обозначение | Знаковое обозначение |
| Эквиваленция Исключающее ИЛИ-НЕ, EQ, XNOR | ↔, |
Является ИСТИННЫМ только при одинаковых простых выражениях.
Таблица истинности логической равнозначности
| A | B | F |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
ПОСТРОЕНИЕ ТАБЛИЦ ИСТИННОСТИ
При решении задач с логическими высказываниями необходимо построение таблиц истинности.
Логическое выражение – это составное выражение, записанное в виде формулы
В логическое выражение могут входить логические переменные, обозначающие высказывания, и знаки логических операций.
Порядок выполнения логических операций (приоритеты):
-
Действия в скобках -
Логическое отрицание (Инверсия) -
Логическое умножение (Конъюнкция) -
Логическое сложение (Дизъюнкция) -
Логическое следование (Импликация) -
Логическая равнозначность (Эквиваленция)
Алгоритм построения таблиц истинности
-
Определить количество логических переменных (n) в логическом выражении (F) -
Определить количество строк в таблице (m) m=2n + 1, где n – количество логических переменных -
Посчитать количество логических операций в логическом выражении -
Определить порядок выполнения логических операций -
Определить количество столбцов: количество логических переменных + количество логических операций -
Выписать наборы входных перемененных -
Заполнить таблицу истинности
ПРИМЕР
Для логического выражения
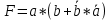 построить таблицу истинности
построить таблицу истинностиРешение
-
Определить количество логических переменных (n) в логическом выражении (F)
У нас две логические переменные, обозначенные латинскими буквами А и В, поэтому n=2.
-
Определить количество строк в таблице (m) m=2n + 1, где n – количество логических переменных
Так как n=2, то m=22+1=5
-
Посчитать количество логических операций в логическом выражении