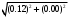Ответы на контрольные вопросы

1. Какие ошибки (погрешности) геодезических измерений называют систематическими, и как свести их влияние к минимуму?

Систематические погрешности входят в каждый результат измерений по строго определенному закону. Они обусловлены влиянием конструкции измерительных приборов, погрешностями градуировки их шкал, износом и т. д. (инструментальные погрешности) или возникают из-за недоучета условий измерений и закономерностей их изменений, приближенности некоторых формул и др. (методические погрешности). Систематические погрешности делятся на постоянные (неизменные по знаку и вели чине) и переменные (изменяющие свою величину от одного измерения к другому по определенному закону).

Такие погрешности заранее определимы и могут быть сведены к необходимому минимуму путем введения соответствующих поправок.

Например, заранее может быть учтено влияние кривизны Земли на точность определения вертикальных расстояний, влияние температуры воздуха и атмосферного давления при определении длин линий светодальномерами или электронными тахеометрами, заранее можно учесть влияние рефракции атмосферы и т. д.

2. Из каких действий складывается приведение теодолита в рабочее положение? Что такое параллакс нитей и как он устраняется.

1) центрирование – установка центра горизонтального круга над вершиной измеряемого угла. Выполняется с помощью нитяного отвеса или оптического центрира, перемещением ножек штатива и с последующим передвижением прибора на головке штатива. Погрешность центрирования зависит от требуемой точности выполняемых работ и не должна превышать 3 мм при измерении горизонтальных углов для решения большинства инженерных задач;

2) горизонтирование – приведение плоскости лимба горизонтального круга в горизонтальное положение, т.е. установка вертикальной оси вращения теодолита в отвесное положение. Для этого устанавливают цилиндрический уровень параллельно двум подъемным винтам и вращая их одновременно в противоположные стороны выводят пузырек уровня на середину ампулы. Затем поворачивают цилиндрический уровень на 90° по направлению третьего подъемного винта и, вращая его, опять выводят пузырек в нульпункт. Эти действия повторяют до тех пор, пока пузырек не будет отклоняться от центра ампулы более чем на одно деление.

---

3) подготовку зрительной трубы для наблюдений по глазу – вращением окуляра (от -5 до +5 диоптрий) до получения четкого изображения сетки нитей на светлом фоне - и по предмету - вращением кремальеры до четкого изображения визирной цели. Если изображение предмета не совпадает с плоскостью сетки нитей, то при перемещении глаза относительно окуляра точка пересечения нитей будет проецироваться на различные точки наблюдаемого предмета. Возникает параллакс, который устраняется небольшим поворотом кремальеры

3. В чём суть измерения горизонтального угла способом приемов. Ответ дополнить схемой.

Прием состоит из двух полуприемов. Первый полуприем выполняют при положении вертикального круга слева от зрительной трубы. Закрепив лимб и открепив алидаду, наводят зрительную трубу на правую визирную цель (точка А рис. 1). После того как наблюдаемый знак попал в поле зрения трубы, зажимают закрепительные винты алидады и зрительной трубы и, действуя наводящими винтами алидады и трубы, наводят центр сетки нитей на изображение знака и берут отсчёт по горизонтальному кругу (отсчет а). Затем, открепив трубу и алидаду, наводят трубу на левую визирную цель (точка В). и берут второй отсчёт (отсчет в). Разность первого и второго отсчётов даёт величину измеряемого угла.

β = а – b

Если первый отсчёт оказался меньше второго, то к нему прибавляют 360º°, тогда: β = (а + 360°) – b

Второй полуприем выполняют при положении вертикального круга справа, для чего переводят трубу через зенит. Чтобы отсчёты отличались от взятых в первом полуприеме, смещают лимб на несколько градусов. Затем измерения выполняют в той же последовательности, как в первом полуприеме. Если результаты измерения угла в полуприёмах различаются не более двойной точности прибора (то есть 1' для теодолита Т30), вычисляют среднее, которое и принимают за окончательный результат.


Рис. 1 Схема измерения угла способом приемов:
а – при размещении нуля лимба вне измеряемого угла;
б – при размещении нуля лимба внутри измеряемого угла

Во избежание появления ошибки, связанной с наклоном вех, визирование производят на нижнюю часть вехи или шпильки.

---

Контрольная работа «План теодолитной съемки»

Исходные данные

α_1-2 = 51°36’;

Х₁ = +500.00;

У₁ = +200.00.

Вычисление угловой невязки теодолитного хода

Вычисляем угловую невязка замкнутого хода в соответствии с формулой:

f_β= Σβ_изм – Σβ_теор,

для наших данных имеем:

Σβ_изм=78˚4.5'+120˚35.5'+84˚50.5'+76˚28' = 358˚58.5';

Σβ_теор=180˚(n– 2) = 360˚,

соответственно, получаем:

f_β= 358˚58.5' – 360˚ = –0˚01.5'.

Вычисляем предельно допустимую невязку внутренних углов:

f_{β доп} = ± 2 · 30'' 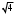= ±2'

Таким образом, полученная угловая невязка не превышает предельно допустимой погрешности (|-01.5'| < 2’) и распределяется равномерно по измеренным горизонтальным углам. Величины поправок подписаны над значениями минут соответствующих измеренных углов.

Результаты введения поправок записываем в графу исправленных горизонтальных углов с точностью до десятых долей угловой минуты. Сумма исправленных внутренних углов равна 360˚, следовательно, поправки введены верно.

Вычисление дирекционных углов сторон хода

Дирекционные углы последующих сторон теодолитного хода вычисляют, применяя значения измеренных внутренних горизонтальных углов. Из схемы вычисления дирекционных углов (рис.1) видно, что дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны, плюс 180°, минус правый исправленный горизонтальный угол между предыдущей и последующей сторонами. Что можно записать в виде формулы:

α_i+1=α_i+180°- β_пр

где βпр. – правые внутренние исправленные углы.



Рис. 1 Схема вычисления дирекционных углов

α_2-3 = 51°36’ +180° - 78°04.9’ = 153°31.1';

α_3-4 = 153°31.1' +180° - 120°35.9’ = 212°55.2'

---

α_4-1 = 212°55.2' +180° - 84°50.9’ = 308°04.3'

α_1-2 = 308°04.3'+180° - 76°28.3’ = 51°36'

Контроль вычисления дирекционных углов соблюден – в конце вычислений получен начальный дирекционный угол α_1-2. Вычисленные значения дирекционных углов всех сторон занесены в одноименную графу.

Вычисление румбов сторон

Связь между дирекционными углами и румбами зависит от четверти, в которой находится заданное направление. Перевод дирекционных углов в румбы выполняется согласно таблицы 1.

Таблица 1

Зависимость дирекционных углов и румбов

Величина дирекционного угла, α	Формула для вычисления румба	Название румба	Четверть	Знаки приращений координат
				ΔХ	ΔУ
0° – 90°	r = α	СВ	I	+	+
90° – 180°	r = 180° – α	ЮВ	II	–	+
180° – 270°	r = α – 180°	ЮЗ	III	–	–
270° – 360°	r = 360° – α	СЗ	IV	+	–

α_1-2 = 51°36’ → 0° < α_1-2<90°,

r_1-2 =51°36’ (СВ);

α_2-3 = 153°31.1' →90° < α_2-3<180°,

r_2-3 =180° – 153°31.1' = 26°28.9'(ЮВ)

r_3-4 =212°55.2' – 180° = 51°55.7'(ЮЗ)

r_4-1 =360° – 308°04.3' = 56°36.0'(СЗ)

Вычисление приращений координат (∆Х,∆У)

Приращения координат теодолитного хода вычисляют в соответствии с формулами прямой геодезической задачи:

ΔХ = d·cosr;

ΔУ = d·sinr.

где d – горизонтальное проложение стороны хода;

r – румб.

Знаки приращений принимаются в зависимости от четверти румба согласно таблицы 1.

ΔХ_1-2 = 146.32·

---

cos51°36’ = +90.89 м ( );

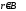ΔУ_1-2 = 146.32·sin51°36’ = +114.67 м ( );

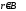ΔХ_2-3 = 71.91·cos26°28.9' = -64.36 м ( );

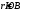ΔУ_2-3 = 71.91·sin26°28.9' = +32.07 м ( ) ;

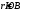ΔХ_3-4 = 111.73·cos32°55.2' = -93.79 м ( );

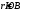ΔУ_3-4 = 111.73·sin32°55.2' = -60.72 м ( );

ΔХ_4-1 = 109.27·cos51°55.7' = +67.38 м ( );

ΔУ_4-1 = 109.27·sin51°55.7' = -86.02 м ( ).

Результаты вычислений занесены в графы Вычисленные приращения координат.

Вычисление невязок координат (fx,fy)

По полученным значениям приращений координат вычисляем линейные невязки по осям x и у:

f_х = ΣΔХ_выч – ΣΔх_теор;

f_у = ΣΔУ_выч – ΣΔу_теор.

Так как теритическая сумма приращений по обеим осям равна нулю, то значения невязок равны сумме вычисленных приращений. Значение сумм записывают внизу граф вычисленных приращений. В нашем примере линейные невязки равны: f_х = +0.12 м и f_у = 0.00 м.

Невязки в приращениях координат обусловлены действием погрешностей измеренияугловисторонхода.Совместноевлияниеневязокприращенийпоосям координат характеризуется линейной невязкой впериметре.

Эту невязку называют абсолютной невязкой f_абс.:

f_абс=

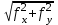
f_абс=

---

Смотрите также файлы

• Методы защиты информации от несанкционированного доступа.docx

• Индивидуальное задание на практику по получению первичных профессиональных умений и навыков, в том числе первичных умений и навыков научно исследовательской деятельности (учебная практика).docx

• Порядок оформления инвентаризаций.docx

• Российский государственный социальный университет Рубежный контроль 2 по дисциплине Возрастная психология и психология развития.docx

• В 20е годы нового начала складываться американская школа автомобильного дизайна она тяготела к доступным массовым автомобилям, с просторными кузовами и мощными, но низкооборотными моторами.docx