Экзаменационные вопросы по дисциплине «Материаловедение наноструктурированных материалов»

1. 
   Динамическое условие существования конденсированной системы.
   

Если кинетическая энергия больше потенциальной, то силы связей будут преодолены. Тогда условие существования конденсированной системы и, в частности, кристалла, может быть записано в виде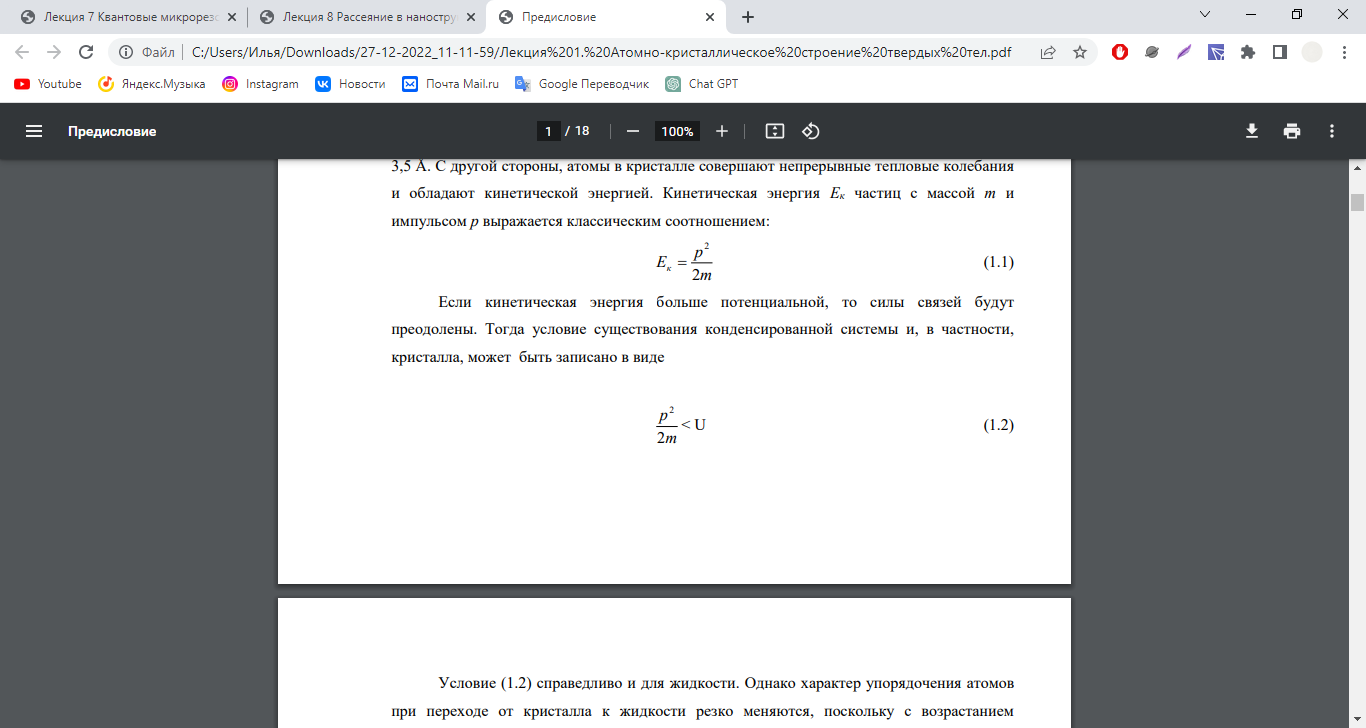

Условие (1.2) справедливо и для жидкости. Однако характер упорядочения атомов при переходе от кристалла к жидкости резко меняются, поскольку с возрастанием импульсов частиц средние расстояния между атомами растут, они все чаще оказываются на дальнем крае минимум кривой U(r). В жидкости статистически образуются некоторые преимущественные конфигурации атомов, и упорядочение тем ниже, чем выше температура.

2. 
   Трансляционная симметрия кристаллов.
   

Кристаллическую структуру, обладающую трансляционной симметрией, можно получить путем периодически повторенной в пространстве элементарной ячейки (элементарной части) кристалла.

Элементарная ячейка должна удовлетворять двум условиям: a) при размножение элементарной ячейки векторами трансляций покрывается все пространство, занимаемое кристаллом;

3. 
   Точечная симметрия кристаллов.Операции и классы точечной симметрии кристаллов.
   

Точечной группой симметрии называется совокупность точечных операций симметрии, совмещающих решетку саму с собой. Общее число независимых точечных групп симметрии кристаллов – 32. Это группы содержат конечное число элементов.

Геометрической симметрией кристаллического пространства (или фигуры) называется свойство пространства (фигуры) совмещаться с самим собой после выполнения некоторых симметрических преобразований.

Операции или преобразования симметрии - это отражения, вращения, переносы (трансляции), приводящие пространство(фигуру) в совмещение с самим собой.

Исчерпывающий список элементов точечной симметрии включает в себя: - плоскость симметрии (плоскость зеркальной симметрии); - центр симметрии (центр инверсии); - оси симметрии определенного порядка; - инверсионные оси симметрии. Плоскостью симметрии m (mirror – зеркало) называется воображаемая плоскость, которая делит фигуру на две зеркально равные части. Плоскость в символике Бравэ обозначается буквой P.

Центром симметрии 1 (С в символике Бравэ) называется особая точка в центре фигуры, характеризующаяся тем, что любая проведенная через нее прямая встречает одинаковые (соответственные, гомологичные) точки по обе стороны и на равных расстояниях от центра.

Осью симметрии n (n-го порядка) называют прямую линию, при повороте вокруг которой на определенный угол φ фигура совмещается сама с собой. Число n (порядок оси) показывает, сколько раз фигура совмещается сама с собой при повороте вокруг этой оси на 360° (φ=2π/n). В символике Бравэ ось симметрии n-го порядка обозначается символами Ln.

Инверсионная ось симметрии n представляет собой произведение оси симметрии и центра симметрии. Под операцией произведения точечных элементов симметрии будем понимать результат симметричного преобразования, полученный последовательным выполнением обоих элементов симметрии. При этом должны образоваться качественно новые элементы симметрии. В символике Бравэ ось симметрии n порядка обозначается символом n L .

4. 
   Классификация кристаллов по группам симметрии.
   

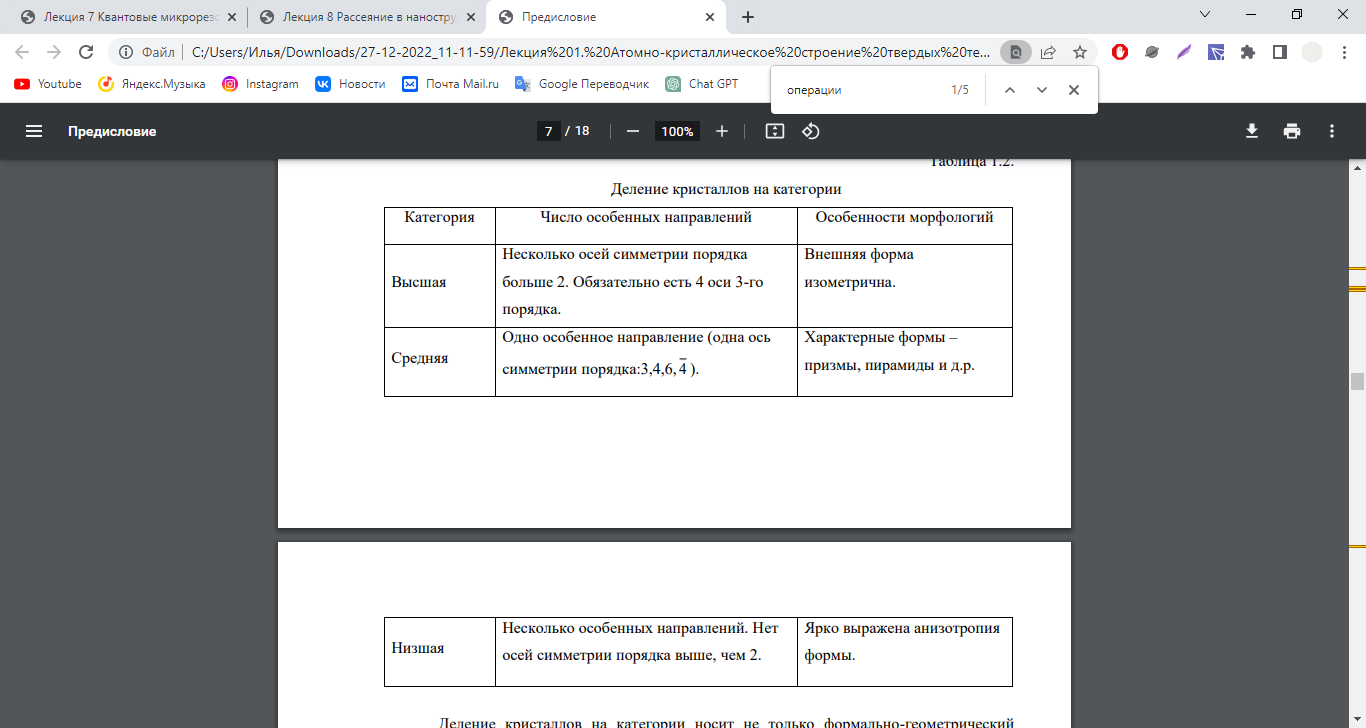
Кристаллы делят также на 7 сингонией (сингония в дословном переводе – сходноугольность). В одну сингонию объединяют кристаллы, у которых одинакова симметрия элементарных ячеек и одинакова система координат. В высшей категории одна сингония – кубическая. Прямоугольная система координат: а=b=c, α = β = γ = 90°, элементарная ячейка представляет собой куб. Оси X, Y, Z параллельны трем взаимно перпендикулярным осям симметрии 4, или 4 , или 2 порядка. К средней категории относят три сингонии: 1. Тригональная. Для нее выполняется: а=b≠c, α=β=90°, γ=120°. Система координат не прямоугольная, строится на ортах различной длины. За ось Z принимают ось симметрии 3, или 3 порядка, оси X, иY лежат в плоскости, перпендикулярной оси Z и выбираются как перпендикуляры к плоскости симметрии (если есть плоскости), либо совпадают с осями 2 порядка. 2. Тетрагональная. Для нее выполняется: а=b≠c, α=β=γ= 90°.Система координат прямоугольная и строится на ортах различной длины. За ось Z принимают ось симметрии 4, или 4 , оси X иY лежат в плоскости, перпендикулярной оси Z и выбираются как перпендикулярны к плоскостям симметрии (если есть плоскости), либо совпадают с осями 2 порядка. 3. Гексагональная. Для нее выполняется: а=b≠c, α=β=90°, γ=60°. Система координат не прямоугольная, строится на ортах различной длины. За ось Z принимают ось симметрии 6 или 6 , оси X и Y лежат в плоскости, перпендикулярной оси Z и выбираются как перпендикуляры к плоскостям симметрии (если есть плоскости), либо совпадают с осями 2 порядка. При описании тригональных и гексагональных кристаллов может использоваться также четырехосная система координат (система Бравэ), когда ось Z направлена вдоль единичного направления, а оси X,Y и U выбираются вдоль осей 2 , либо вдоль нормалей к плоскостям. К низшей категории также относят три сингонии. 1. Ромбическая. Для нее выполняется: а≠b≠c, α=β=γ=90° Система координат прямоугольная, строится на ортах различной длины. Чтобы различать оси системы координат, принято, чтобы выполнялось условие: b>a>c.Оси выбирают параллельно осям симметрии 2 или вдоль перпендикуляров к плоскостям симметрии. 2. Моноклинная. Для нее выполняется : а≠b≠c, α=γ=90°, угол β - произволен. Ось Y выбирают вдоль оси симметрии 2, или вдоль перпендикуляра к плоскости симметрии. Оси X, Z лежат в плоскости, перпендикулярной оси 2. 3. Триклинная. Для нее выполняется: а≠b≠c, α≠β≠γ≠90°. Оси кристаллографической системы координат не заданы элементами симметрии, а выбираются вдоль ребер кристалла или элементарной ячейки при выполнении условия: b>a>c.

5. 
   Пространственная симметрия кристаллов.
   

Симметрия структуры кристаллов (пространственная симметрия). В пространственных группах симметрии кристаллов к конечным преобразованиям, входящим в симметрию точечной группы, добавляются еще трансляционные преобразования. Группа трансляций - это бесконечно повторяющийся перенос атомов (групп атомов) вдоль какой-либо прямой на одно и то же определенное расстояние, называемое периодом трансляции.

Плоскость скользящего отражения - это совокупность совместно действующих плоскости симметрии и параллельного ей переноса на величину, равную доле периода трансляции вдоль плоскости. Ориентированная в плоскости YZ плоскость скользящего отражения обозначается символом а, в плоскости XZ – символом b, в плоскости XYсимволом с.

Произведение доли периода трансляции на поворот вокруг оси порождает винтовой поворот. Винтовой осью симметрии называется совокупность оси симметрии и переноса вдоль этой оси, действующих совместно. После данной операции симметрии исходная точка должна совместится с точкой, идентичной первой, но отстоящей на один или несколько периодов трансляции.

Пространственной группой симметрии называется сочетание всех возможных бесконечных преобразований симметрии кристаллической структуры. Пространственная группа симметрии характеризует симметрии кристаллической структуры, так же, как точечная группа симметрии характеризует симметрию внешней формы кристалла и симметрию его макроскопических физических свойств.

6. 
   Электронная конфигурация атома, энергетические зоны. Валентная зона и зона проводимости.
   

Электронной конфигурацией атома называется обозначение того, как электроны распределяются по энергетическим уровням (электронным оболочкам), подуровням и орбиталям.

В твёрдом теле энергетический спектр электронов существенно иной, он состоит из отдельных разрешённых энергетических зон, разделённых зонами запрещённых энергий.

Зо́на проводи́мости — в зонной теории твёрдого тела первая зона, целиком или большей частью расположенная над уровнем Ферми. Является энергетически разрешённой для электронов зоной, то есть доступным для электронов диапазоном энергий, в полуметаллах, полупроводниках и диэлектриках.

Вале́нтная зо́на — энергетическая область разрешённых электронных состояний в твёрдом теле, заполненная валентными электронами. В зонной теории это первая зона (если двигаться сверху вниз), целиком или большей частью расположенная ниже уровня Ферми.

7. 
   Классификация твердых тел.
   

Все твёрдые тела делятся на кристаллические и аморфные. Мы рассмотрели, в чём их сходство и различие.   Кристаллы – это твёрдые тела, атомы или молекулы которых занимают определённые, упорядоченные положения в пространстве. Кристаллические тела делятся на монокристаллы и поликристаллы. Монокристаллы – одиночные кристаллы. Монокристаллами наз. одиночные кристаллы, имеющие макроскопическую упорядоченную кристаллическую решетку. Поликристаллы – это твёрдые тела, состоящие из большого числа кристаллов, беспорядочно ориентированных друг относительно друга.  Одним из наиболее существенных свойств монокристаллов является анизотропия – зависимость (неодинаковость) физических свойств кристалла от направления. Но в отличии от монокристаллов, поликристаллы  изотропны, т.е. физические свойства одинаковые по всем направлениям. Это объясняется тем, что кристаллы  внутри располагаются беспорядочно, и каждый в отдельности обладает анизотропией, а в целом кристалл изотропен. Свойства кристаллических тел:  правильность геометрической формы, постоянная температура плавления, анизотропия свойств.

Аморфные тела – это твёрдые тела, где сохраняется только ближний порядок в расположении атомов. (Кремнезём, смола, стекло, канифоль, сахарный леденец). Отличие в характере движения: частицы не только совершают колебательные движения, но совершают скачки (движения характерные для жидкой фазы состояния вещества) Свойства аморфных тел: отсутствие симметрии, отсутствие постоянной температуры плавления, изотропия свойств.

Аморфные тела – жидкости с очень большой вязкостью (при низких температурах ведут себя как кристаллические тела, при высоких температурах и постоянной нагрузке – как жидкости).
В аморфных телах не наблюдается строгого порядка в расположении их частиц.

8. 
   Чистые и примесные полупроводники.
   

Различают собственные и примесные полупроводники. К числу собственных относятся чистые полупроводники (т.е полупроводники без примесей или с концентрацией примеси настолько малой, что она не оказывает существенного влияния на удельную проводимость полупроводника). Проводимостьтаких чистых полупроводников называетсясобственной.

В примесных полупроводниках электрические свойства определяются примесями, вводимыми искусственно в очень малых количествах. Проводимость полупроводников, обусловленная примесями, называется примесной проводимостью

9. 
   Температурная зависимость электропроводности твердых тел.
   

 электропроводность полупроводника определяется концентрациями свободных носителей заряда в нем и их подвижностями. Это будет справедливым и для электропроводности металлов. Но в металлах концентрация электронов очень велика 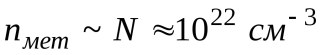 и не зависит от температуры образца.Подвижность электронов в металлах убывает с температурой вследствие увеличения числа столкновений электронов с тепловыми колебаниями кристаллической решетки, что и приводит к уменьшению электропроводности металлов с ростом температуры. В полупроводниках же основной вклад в температурную зависимость электропроводности вносит зависимость от температуры концентрации носителей заряда.

10. 
    Условия проявления и особенности влияния размерных эффектов в наноматериалах.
    

Размерные эффекты наблюдаются при уменьшении размера структурных элементов: частиц, кристаллитов и зерен ниже некоторой пороговой величины. Такие эффекты появляются, когда средний размер кристаллических зерен не превышает 100 нм, и наиболее отчетливо проявляются при размерах зерен менее 10 нм. Квантовые размерные эффекты проявляются в электронных свойствах вещества или материала и связаны с уменьшением размерности электронного газа, что приводит к изменению энергетического спектра (например, см. голубой сдвиг).

Влияние размера частиц на физико-химические свойства вещества можно объяснить наличием поверхностного давления, действующего на вещество. Это дополнительное давление, которое обратно пропорционально размеру частиц, приводит к увеличению энергии Гиббса и, как следствие, повышению давления насыщенных паров над наночастицами, уменьшению температур кипения жидкой фазы и плавления твердой (рис.). Изменяются и другие термодинамические характеристики — константы равновесия и стандартные электродные потенциалы. Так, при уменьшении размера наночастиц серебра стандартный потенциал пары Ag+/Ag может стать отрицательным, и серебро будет растворяться в разбавленных кислотах с выделением водорода.

11. 
    Квантовое ограничение и туннелированиев наноматериалах.
    

Квантовое туннелирование — это эффект, при котором квантовые частицы могут проходить через барьеры, высота которых больше, чем энергия частиц.

Конечное минимальное значение энергии электронов и дискретность разрешенных энергетических состояний для них в наноструктуре, возникающие как следствие квантово-волнового поведения электрона в замкнутом пространстве является эффектом квантового ограничения. Он характерен как для электронов, так и для дырок. В твердых телах квантовое ограничение может быть реализовано в трех пространственных направлениях. То количество направлений в твердотельной структуре, в которых квантовое ограничение отсутствует, используется в качестве критерия для квалификации элементарных наноструктур по следующим группам – квантовые пленки, квантовые проволоки, квантовые точки

12. 
    Баллистический транспорт и квантовая интерференция.
    

В наноструктурах с размером меньше длины свободного пробега перенос носителей заряда происходит без их рассеяния. Такой перенос называют баллистическим транспортом (ballistic transport). Здесь важно соотношение между размерами наноструктуры и характерными длинами свободного пробега для упругого и неупругого рассеяния носителей заряда.

Квантовая интерференция представляет собой один из экзотических эффектов, проявляющихся при наблюдении магнитных осцилляций в нормальных металлах. Он возникает вследствие интерференции электронных волновых пакетов, движущихся в магнитном поле в одном направлении вдоль незамкнутых орбит импульсного пространства, связанных магнитопробойными переходами. Выражается такой эффект в появлении в спектре осцилляций Шубникова - де Гааза частот, для которых нет разрешенных орбит. При этом в спектре осцилляций де Гааза - ван Альфена такие частоты отсутствуют. В обычных трехмерных металлах чрезвычайно редко реализуются сечения поверхности Ферми, для которых выполняются все условия наблюдения квантовой интерференции, что делает данный эффект практически недоступным для детального исследования. Напротив, в некоторых органических квазидвумерных металлах, синтезированных на основе ЕТ (бис- (этилендитио)тетратиафульвален) поверхность Ферми изначально устроена таким образом, что условия наблюдения квантовой интерференции выполняются в широком интервале направлений магнитного поля. 

13. 
    Квазичастицы. Экситоны Френкеля.
    

http://solidstate.karelia.ru/p/tutorial/ftt/Part11/part11.3.3.htm

Экситон Френкеля — предельный случай реализации экситона Ванье — Мотта. Электрон и дырка, составляющие экситон Френкеля, принадлежат одному узлу или соседним узлам кристаллической решётки, таким образом, радиус экситона составляет величину порядка периода решётки.

ФРЕНКЕЛЯ ЭКСИТОН

- модель экситона, отвечающая переносу по кристаллу внутриатомного (внутримолекулярного) возбуждения. Ф. э, часто наз. также э к с и т о н о м м а л о г о р а д и у с а. Представляет собой предельный случай, обратный Ванье- Momma экситону, иначе э к с и т о-н у б о л ь ш о г о р а д и у с а. Ф. э. могут существовать в кристаллах, в к-рых внутримолекулярное взаимодействие значительно сильнее межмолекулярного.

14. 
    Квазичастицы. Экситоны Ванье-Мотта.
    

Квазичастицы (от квази... и частицы), одно из фундаментальных понятий теории конденсированного состояния вещества, в частности теории твёрдого тела. Частицы конденсированной среды подчиняются законам квантовой механики; поэтому свойства совокупности частиц, составляющих твёрдое тело (или жидкость), могут быть поняты лишь на основе квантовых представлений. Развитие квантовой теории конденсированных сред привело к созданию специальных физических понятий, в частности к концепции К. — элементарных возбуждений всей совокупности взаимодействующих частиц.

Экситон Ванье — Мотта — экситон, радиус которого значительно превышает характерный период решётки кристалла (в отличие от экситонов Френкеля).

Экситоны Ванье — Мотта существуют в полупроводниках за счёт высокой диэлектрической проницаемости последних. Высокая диэлектрическая проницаемость приводит к ослаблению электростатического притяжения между электроном и дыркой, что и приводит к большому радиусу экситона.

15. 
    Гетероструктуры.
    

Гетероструктура – это контакт между полупроводниками с различной шириной запрещенной зоны.

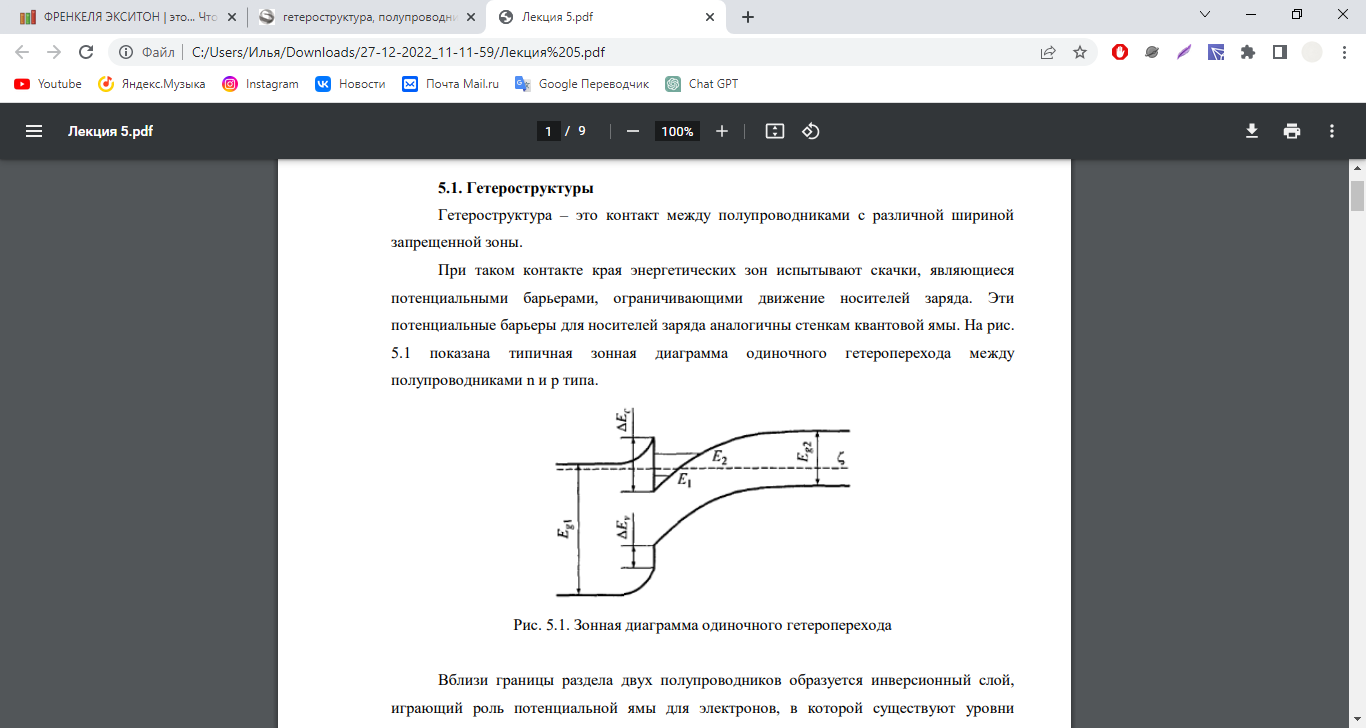
При таком контакте края энергетических зон испытывают скачки, являющиеся потенциальными барьерами, ограничивающими движение носителей заряда. Эти потенциальные барьеры для носителей заряда аналогичны стенкам квантовой ямы

Вблизи границы раздела двух полупроводников образуется инверсионный слой, играющий роль потенциальной ямы для электронов, в которой существуют уровни размерного квантования.

16. 
    Сверхрешетки: основные типы и современные технологические решения.
    

Искусственная структура, состоящая из совокупности квантовых объектов (квантовых ям, нитей, точек), между которыми возможен перенос носителей заряда, называется сверхрешеткой. Существуют сверхрешетки периодические (квантовые объекты чередуются периодически), непериодические и квазипериодические.

Перенос носителей заряда в сверхрешетках между отдельными квантовыми объектами называется вертикальным в отличие от переноса в изолированных квантовых ямах и квантовых нитях, где он является планарным. В связи с этим сверхрешетки называют низкоразмерными структурами с вертикальным переносом. Если в рассматриваемых структурах вертикальный перенос между квантовыми объектами невозможен, их называют структурами с множеством изолированных квантовых объектов. Свойства таких структур, как правило, совпадает со свойствами отдельных квантовых объектов, поскольку вклады от всех них просто суммируются.

Полупроводниковые композиционные сверхрешетки Композиционными сверхрешетками называются структуры с периодически повторяющимися слоями различных полупроводников, т.е. решетки на основе гетероструктур

Сверхрешетки типа полуметалл-полупроводник Полуметаллами в физике твёрдого тела называются различные вещества, занимающие по электрическим свойствам промежуточное положение между металлами и полупроводниками. В отличие от полупроводников полуметаллы обладают электрической проводимостью вблизи абсолютного нуля температуры, в то время как полупроводники в этих условиях изоляторы

Сверхрешетки на основе кремния и структур металл-диэлектрик-полупроводник (МДП-структур) Сверхрешетку на основе кремния также можно получить с помощью МОП-структуры (металл-оксид кремния-кремний), которая является частным случаем МДП-структур. Сверхрешетки на основе МДП-структур получаются с помощью нанесения сеточного электрода в виде тонких параллельных металлических нитей на поверхность диэлектрика. При подаче на этот электрод напряжения порядка ширины запрещенной зоны полупроводника образуется одномерный периодический потенциал для электронов инверсионных слоев.

Легированные сверхрешетки Периодическими легированными сверхрешетками называются структуры, состоящие из периодически чередующихся слоев одного и того же полупроводника, легированных донорами и акцепторами.

Композиционно-легированные сверхрешетки Сруктуры из разных полупроводников, в которых легированы слои одного из полупроводников или обоих (в этом случае тип проводимости слоев должен быть разным) называются композиционно-легированными.

Квазипериодические и непериодические СР К квазипериодическим относятся такие сверхрешетки, которые образуются чередованием двух структурных элементов А и В, каждый из которых имеет свои характеристики потенциальных барьера и ямы.

17. 
    Квантование энергии и плотность состояний в сверхрешетках.
    

18. 
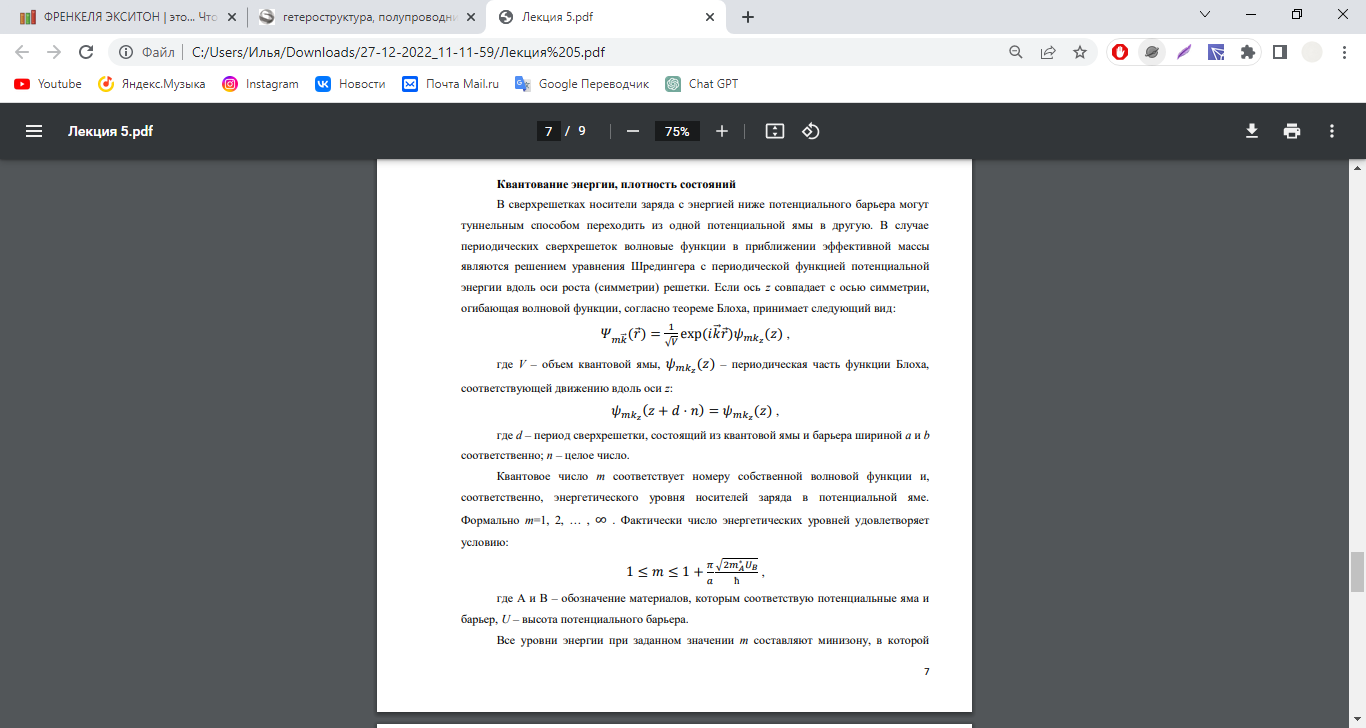
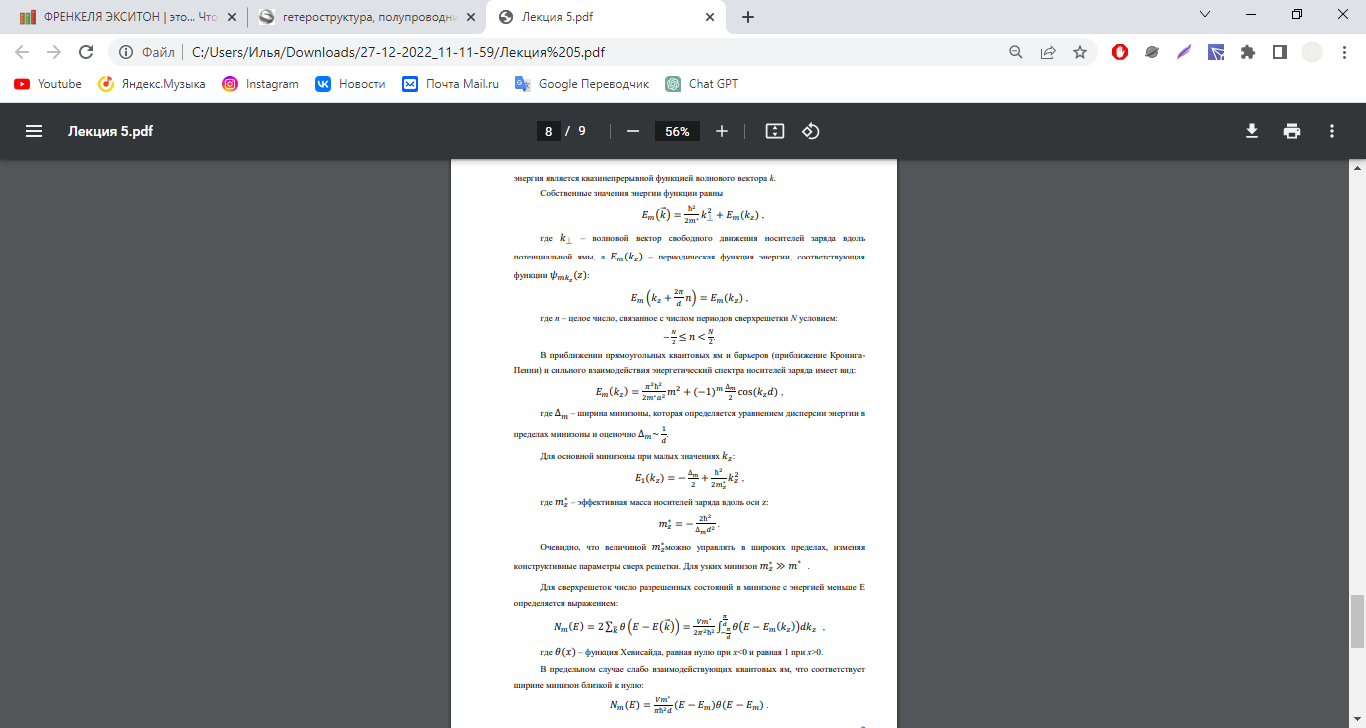
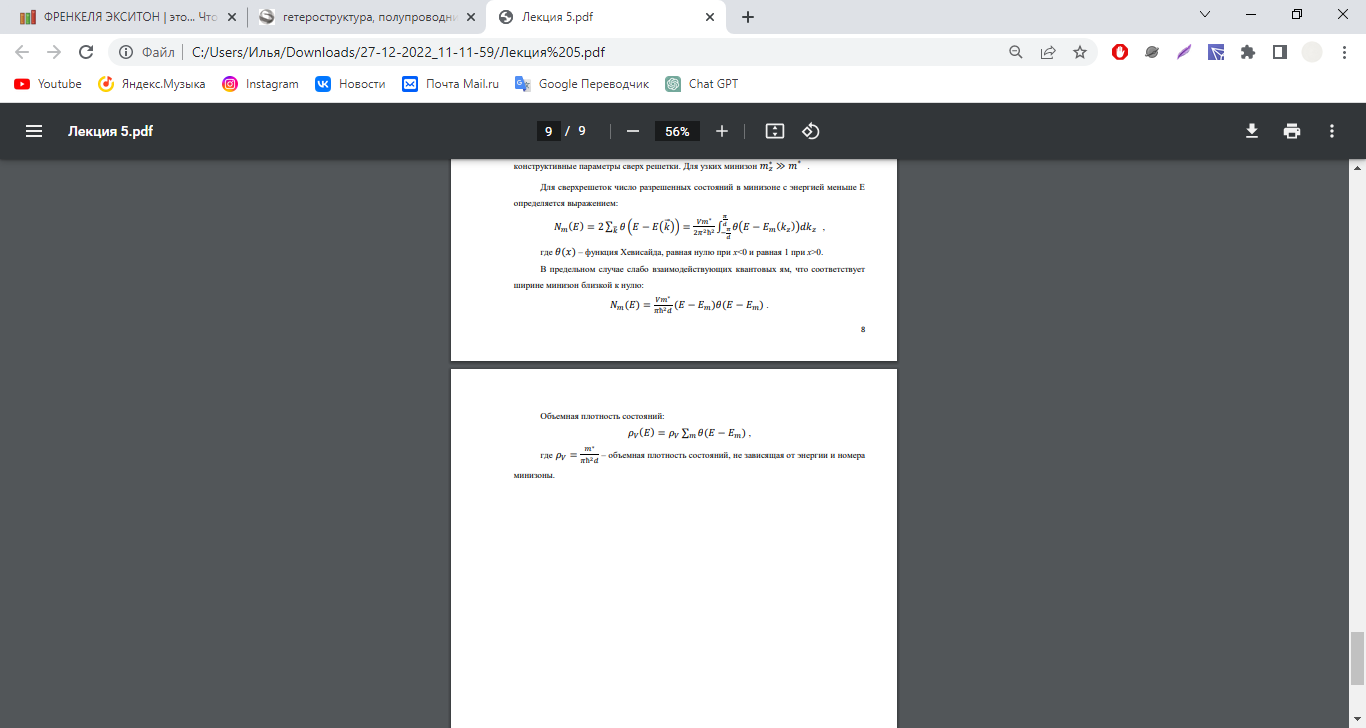
    Фотонные кристаллы.
    

Фотонный кристалл – это материал, структура которого характеризуется периодическим изменением показателя преломления в пространственных направлениях. Фотонные кристаллы можно разделить на три основных класса:

1. Одномерные фотонные кристаллы – структуры, в которых показатель преломления периодически изменяется в одном пространственном направлении. Такие фотонные кристаллы представляют собой тонкослоистую структуру с чередующимися слоями из двух или более материалов. В таких периодических структурах характер распространения световых волн существенно изменяется из-за явлений интерференции и дифракции. Например, многослойные отражающие покрытия используются для изготовления диэлектрических зеркал и интерференционных фильтров, а объемные брэгговские решетки используются в качестве спектральных селекторов и фильтров.

2. Двумерные фотонные кристаллы – структуры, в которых коэффициент преломления периодически изменяется в двух пространственных направлениях. При этом форма областей с различными показателями преломления может быть любой (окружности, эллипсы и т. д.). К двумерным фотонным кристаллам можно отнести упорядоченные массивы цилиндров или периодические системы цилиндрических отверстий с поперечными размерами много меньше продольного. 3. Трёхмерные фотонные кристаллы – структуры, в которых показатель преломления периодически изменяется в трёх пространственных направлениях. Характерной особенностью любого фотонного кристалла является обладание фотонной запрещенной зоной, то есть диапазоном частот, внутри которого электромагнитная волна (фотон) не может распространяться внутри фотонного кристалла. В частности, излучение, спектр которого лежит в фотонной запрещенной зоне, не может проникать в фотонный кристалл и поэтому оно полностью отражается от его границы. Фотонная запрещенная зона образуется в результате интерференции световых волн, отраженных от областей с различными показателями преломления.

19. 
    Квантовые микрорезонаторы.
    

Резонатор – это колебательная система, в которой могут распространяться только колебания с определенными (резонансными) частотами. Обычно резонатор имеет дискретный спектр резонансных частот. В оптике обычно используются открытые резонаторы. Резонатор может использоваться для накопления энергии при совпадении резонансной частоты и частоты падающей электромагнитной волны.

Простейшим микрорезонатором является резонатор Фабри-Перо, представляющий собой систему из двух плоских зеркал (рис. 7.1). В качестве квантового микрорезонатора может использоваться одномерный фотонный кристалл с дефектом или брэгговскими зеркалами.

Микрорезонаторы со встроенной квантовой ямой, или квантовые микрорезонаторы, являются перспективными устройствами для оптоэлектроники: эти структуры перспективны для создания низкопороговых вертикально излучающих

 лазеров; фундаментальные вопросы взаимодействия двумерных фотонов с веществом открыли

 новый раздел в квантовой электродинамике; квантовые микрорезонаторы представляют новые возможности для нелинейной оптики,

 так как нелинейный отклик сильнее зависит от константы экситон-фотонной связи.

20. 
    Рассеяние света. Релеевское рассеяние и рассеяние Ми.
    

Наличие флуктуаций показателя преломления приводит к рассеянию света. Флуктуации можно разделить на два вида: 1) динамические, например, колебания решетки (фононы), поляритоны, плазмоны, экситоны и др.; 2) статические, например, неоднородности плотности, химического состава, температуры и т.п.

В объемных полупроводниках присутствуют следующие компоненты рассеяния света: 1. рассеяние на свободных носителях, включая рассеяние на флуктуациях плотности заряда (одночастичные возбуждения и плазмоны) и флуктуациях спиновой плотности (переходы с переворотом спина);

2. рассеяние на фононах, оптических (рамановское, или комбинационное, рассеяние) или акустических (рассеяние Мандельштама-Бриллюэна);

3. рассеяние на статических дефектах (релеевское рассеяние).

Рэлеевское рассеяние – это упругое рассеяние света на оптических возбуждающегонеоднородностях, размеры которых значительно меньше длины волны света.



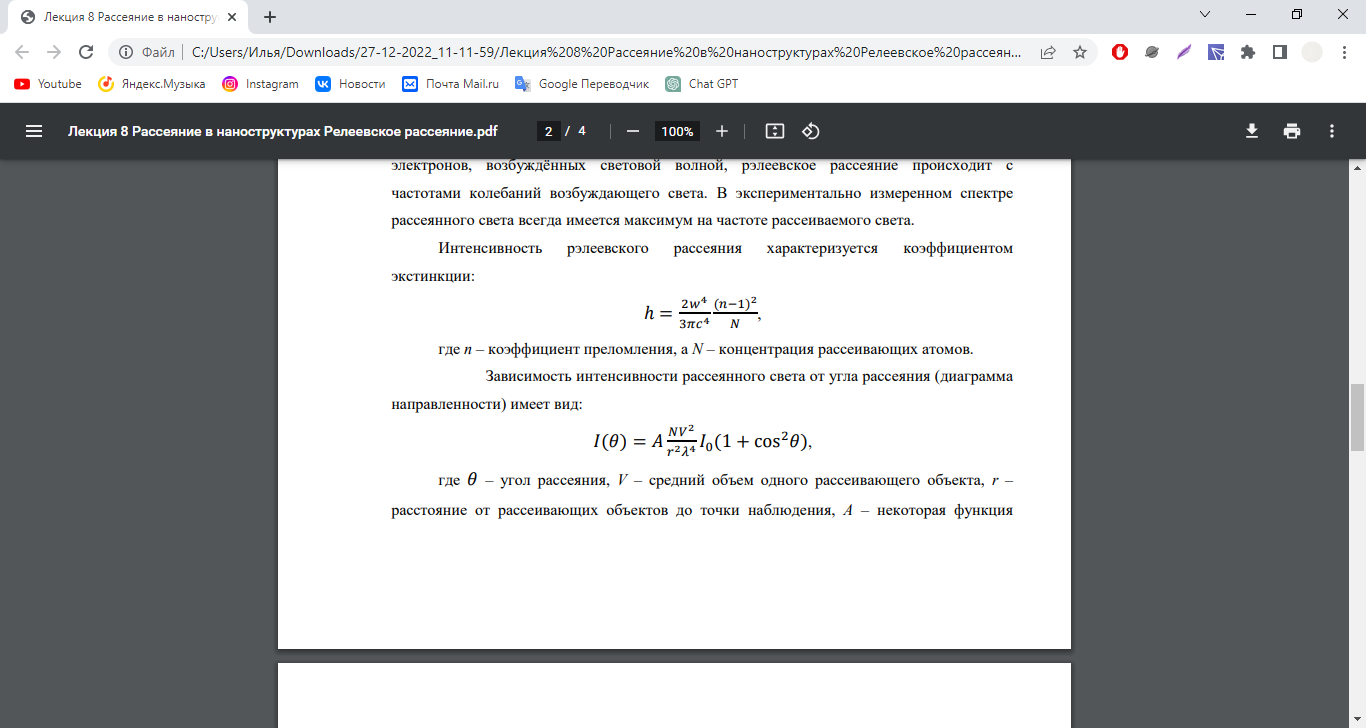
Рассеяние Ми – это упругое рассеяние на частицах сферической формы. Рассеяние Ми наблюдается в случае, когда размеры оптических неоднородностей d сопоставимы с длиной волны света (d

λ). Для рассеяния Ми характерна более слабая по сравнению с рассеянием Рэлея частотная зависимость.

---

21. 
    Рассеяние Мандельштама-Бриллюэна.
    

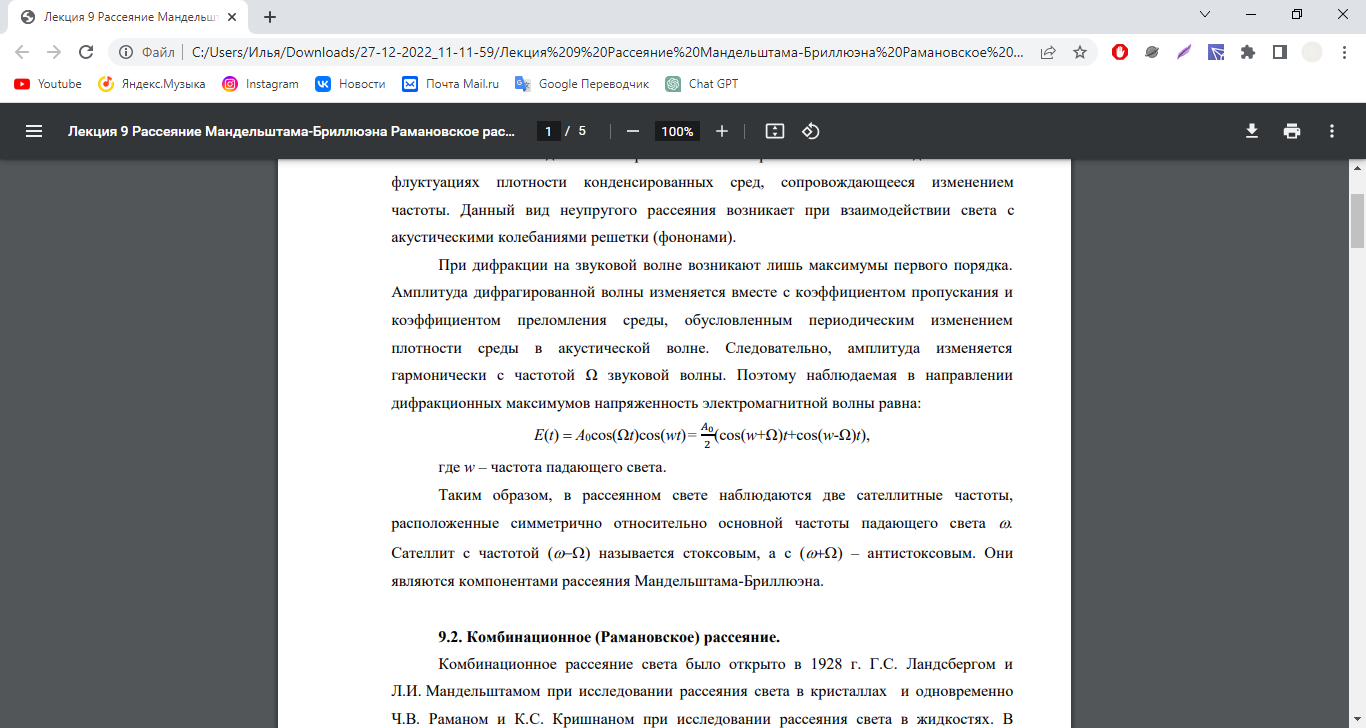
Рассеяние Мандельштама-Бриллюэна – это рассеяние света на адиабатических флуктуациях плотности конденсированных сред, сопровождающееся изменением частоты. Данный вид неупругого рассеяния возникает при взаимодействии света с акустическими колебаниями решетки (фононами).

22. 
    Комбинационное рассеяние света.
    

Основные физические принципы, на которых строится классическая теория комбинационного рассеяния света, могут быть сформулированы следующим образом. 1. Рассеяние света возникает вследствие вынужденных колебаний дипольного момента молекулы, индуцируемого полем падающей световой волны. 2. Свет в видимой и ближней ультрафиолетовой областях спектра рассеивается в основном электронной оболочкой молекулы, а ядра атомов смещаются незначительно. 3. Комбинационное рассеяние света возникает вследствие того, что движение электронов в молекуле связано с движением ее ядер, а именно: взаимное расположение ядер определяет то внутреннее поле, в котором находится электронное облако. Способность электронного облака деформироваться под действием электрического поля световой волны зависит от конфигурации ядер в данный момент. При колебаниях ядер около положения равновесия способность электронного облака деформироваться изменяется с частотой колебаний ядер. В свою очередь при деформации электронного облака могут возникнуть колебания ядерного скелета молекулы. Таким образом, комбинационное рассеяние света можно рассматривать как результат модуляции индуцированного дипольного момента колебаниями скелета молекулы.

23. 
    Классическая теория теплоемкости. Закон Дюлонга и Пти.
    

В основе классической теории теплоемкости твердых тел лежит закон равномерного распределения энергии по степеням свободы. Однородное твердое тело рассматривается как система независимых друг от друга частиц, имеющих три степени свободы и совершающих тепловые колебания с одинаковой частотой. Расположение частиц в узлах кристаллической решетки отвечает минимуму их взаимной потенциальной энергии. При смещении частиц из положения равновесия в любом направлении появляется сила, стремящаяся вернуть частицу в первоначальное положение, вследствие чего возникают колебания частицы. Колебание вдоль произвольного направления можно представить как наложение колебаний вдоль трех взаимно перпендикулярных направлений. Поэтому каждой частице в кристалле следует приписать три колебательные степени свободы

---

На каждую колебательную степень свободы приходится в среднем энергия k_BT – ½ k_BT в виде кинетической энергии и ½ k_BT в виде потенциальной энергии. Следовательно, на каждую частицу в узле кристаллической решетки приходится в среднем энергия, равная 〈????〉= 3kBT.

Закон Дюлонга и Пти: Молярная теплоемкость химически простых тел в кристаллическом состоянии одинакова и равна 3R.

Однако, как было экспериментально установлено, теплоемкость кристаллов зависит от температуры. Характер этой зависимости приведен на графике. Вблизи абсолютного нуля теплоемкость всех тел пропорциональна Т 3 и только при достаточно высокой, характерной для каждого вещества температуре, закон выполняется с довольно хорошим приближением. Для многих веществ это достигается уже при комнатной температуре. Однако, например, алмаз имеет при комнатной температуре теплоемкость, равную примерно 0,7R, а значения 3R она достигает при температуре порядка 1000˚С.

24. 
    Теория теплоемкости Эйнштейна.
    

Средняя энергия колебательного движения 〈????〉= 3kT получается в предположении, что энергия гармонического осциллятора может принимать непрерывный ряд значений. Из решения уравнения Шредингера для квантового гармонического осциллятора установили, что колебательная энергия квантуется. Энергия гармонического квантового осциллятора может принимать значения:

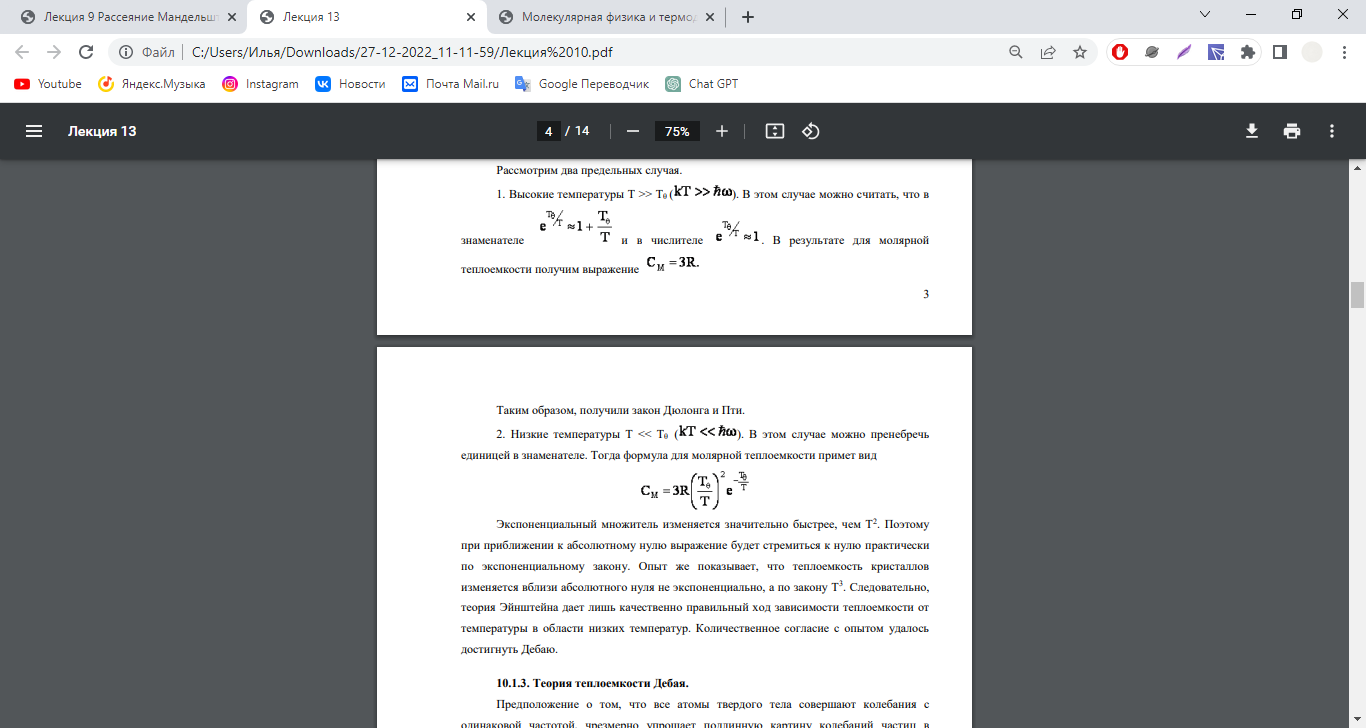
Это приводит к тому, что средняя энергия колебания оказывается отличной от kT. Теория теплоемкости кристаллических тел, учитывающих квантование колебательной энергии, была создана Эйнштейном в 1907 г. В первоначальной квантовой теории теплоемкости твердых тел Эйнштейн отождествил кристаллическую решетку из N атомов с системой 3N квантовых гармонических осцилляторов, колебания которых происходят независимо друг от друга с одинаковой собственной частотой ω. Эйнштейн исходил из значения энергии гармонического осциллятора, предложенного Планком в теории теплового излучения,

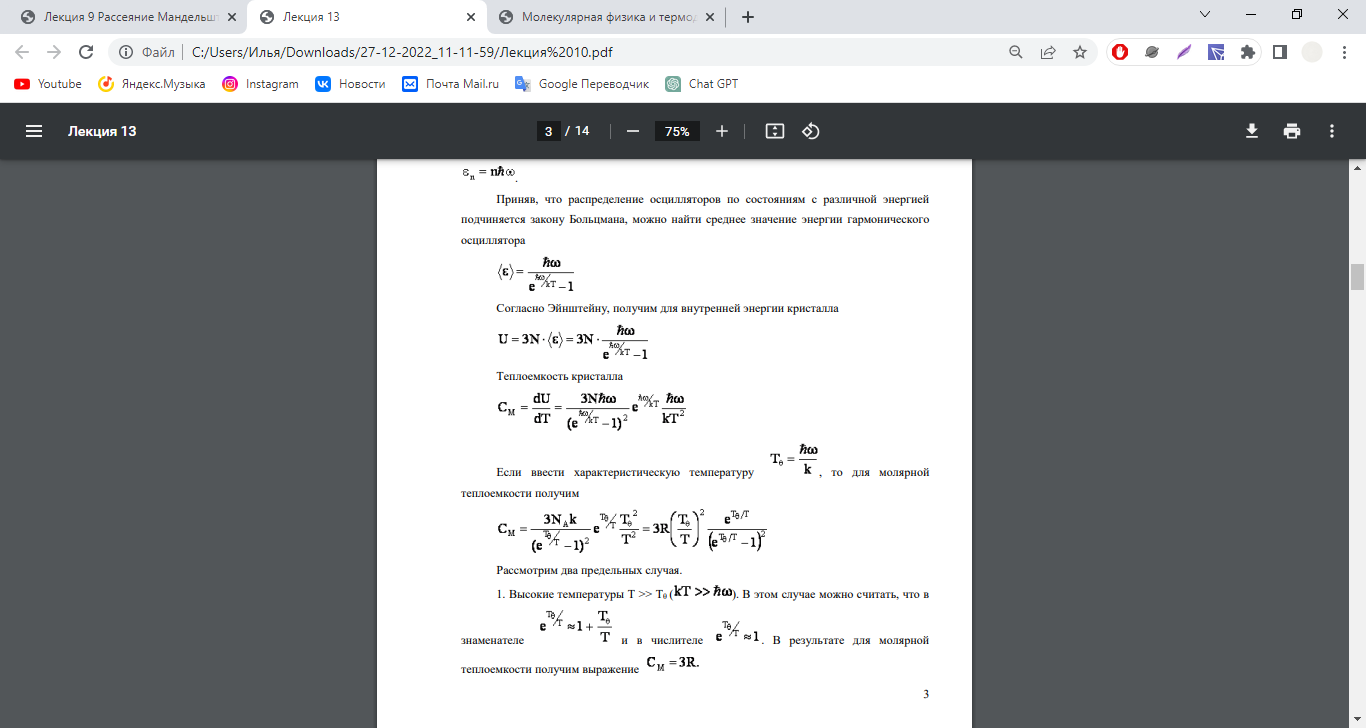
Приняв, что распределение осцилляторов по состояниям с различной энергией подчиняется закону Больцмана, можно найти среднее значение энергии гармонического осциллятора

---

25. 
    Теория теплоемкости Дебая.
    

Квантовая теория теплоёмкостей Дебая

В термодинамике и физике твёрдого тела модельДебая — метод развитый Дебаем в 1912 г. для оценки фононного вклада в теплоёмкость твёрдых тел. Модель Дебая рассматривает колебания кристаллической решётки как газ квазичастиц — фононов. Эта модель правильно предсказывает теплоёмкость при низких температурах, которая пропорциональна T³. В пределе высоких температур теплоёмкость стремится к 3R, согласно закону Дюлонга — Пти.

При тепловом равновесии энергия E набора осцилляторов с различными частотами   равна сумме их энергий:



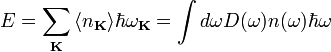
где D(ω) — число мод нормальных колебаний на единицу длины интервала частот, n(ω) — количество осцилляторов в твёрдом теле, колеблющихся с частотой ω.

Функция плотности D(ω) в трёхмерном случае имеет вид:



где V — объём твёрдого тела, v — скорость звука в нём.

Значение квантовых чисел вычисляются по формуле Планка:



Тогда энергия запишется в виде





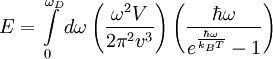
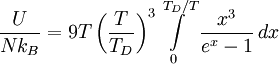
где T_D — температура Дебая, N — число атомов в твёрдом теле, k_B — постоянная Больцмана.

Дифференцируя внутреннюю энергию по температуре получим:

26. 
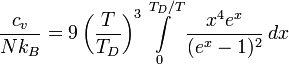
    Тепловые свойства наночастиц в приближении Дебая.
    
27. 
    Ангармонизм колебаний атомов.Фононное взаимодействие.
    

---

При рассмотрении тепловых колебаний в выражении для потенциальной энергии как правило ограничиваются лишь второй производной по межатомным расстояниям. В этом (гармоническом) приближении выполняется закон Гука, а тепловое расширение необъяснимо.

Именно в гармоническом приближении выполняются следующие положения

- адиабатические и изотермические упругие постоянные равны между собой и не зависят от давления и температуры;

- теплоемкость при высоких температурах перестает зависеть от температуры и ???????? = ????_????;

- упругие волны в решетке не взаимодействуют друг с другом и со временем не изменяют свою форму.

В реальных телах ни одно из этих следствий гармонического приближения точно не выполняется. Учет производных третьего и более высокого порядков при теплофизических расчетах соответствует ангармоническому приближению. Ангармонизм колебаний атомов приводит к тому, что силовые постоянные, характеризующие величину сил межатомной связи, зависят от амплитуды колебаний, а значит, и частота начинает зависеть от амплитуды смещений. Ангармонизм ведет и к возникновению таких явлений, как тепловое расширение и взаимодействие фононов.

Взаимодействие двух фононов можно, с одной стороны, рассматривать как процесс рассеяния одной волны на периодических неоднородностях, которые создаются другой волной, с другой – как рассеяние двух частиц при их взаимодействиях друг с другом. В результате взаимодействия фононов с частотами ????1 и ????2 возникает третий фонон с частотой ????1 + ????2. Его возникновение происходит в соответствии с законом сохранения энергии и импульса.

28. 
    Ангармонизм колебаний атомов.Тепловое расширение.
    

Таким образом, при увеличении амплитуды колебаний осциллятора с возрастанием температуры происходит увеличение среднего по времени значения его равновесной координаты, т. е. происходит тепловое расширение твердого тела. Для описания теплового расширения твердого тела можно воспользоваться приближенной моделью, в которой решетка заменена на совокупность ангармонических осцилляторов

29. 
    Магнитные свойства наноматериалов.
    

Магнитные свойства наноструктур обладают большим разнообразием и отличаются от свойств объемных материалов. Основной вклад вносят размерные эффекты, влияние поверхности, межкластерные взаимодействия и взаимодействия кластера с матрицей. К магнитным свойствам нанокластеров и наноструктур относятся:

---

Смотрите также файлы

• Объектноориентированное проектирование автоматизированных систем управления.docx

• Блтты саты кшірмелер жне оны ож лік нсасы Онлайн саты кшірмесі. Ож Блтты саты кшіру.rtf

• Национальных счетов и ее показатели.docx

• Реформы Солона.docx

• Законодательный процесс состоит из нескольких последовательных стадий. Эти.docx