1Плотностью распр-я вер-ей непрерыв СВ Х на-ют ф-ю f (х)- первую производную от ф-ии распределения F (х): f (х) = F' (х)

2Теор. Вер-ть того, что непрерыв СВ Х примет знач, принадлеж интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b: Р (а < Х < b) =

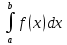
3 Зная плотность распределения f (х), можно найти ф-ию распред-я F (х) по формуле F (х) =

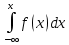
4Свойство1 . Плотность распределения-не отрицательная функция: f (х) 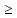0

Свойство 2. Несобственный интеграл от плотности распределения в пределах от - 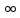до 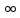равен единице: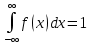

5вероятность того, что СВ примет значение, принадлежащее интервалу (х, х + 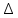х), приближенно равна (с точностью до бесконечно малых высшего порядка относнтельно 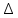х) произведению плотности вероятности в точке х на длину интервала х.

6Распределение вер-ей на-ют равномерным, если на интервале, которому принадлежат все возможные значения случайной вел-ы, плотность распределения сохраняет постоянное значение.

7

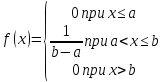
8Х. возможные значения которой принадлежат отрезку [a, b]. на-ют определенный интеграл

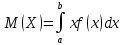
Если возможные значения принадлежат всей оси Ох, то

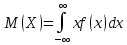
9 Дисперсией на-ют мат-ое ожид квадрата ее отклонения. Если возможные значения Х принадлежат отрезку [а,

---

b], то 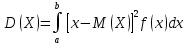если возможные знач принадлежат всей оси х, то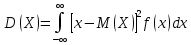

10 Среднее квадратическое отклонение непрерывной случайной вел-ы определяется, как и для вел-ы дискретной, равенством

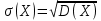
11

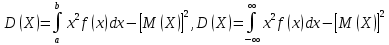
12Нормальным на-ют распределение вероятностей непрерывной случайной вел-ы, которое описывается плотностью

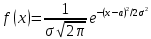
13

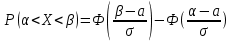
14 В частности, при a=0

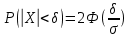
15 если СВ распределена нормально, то абсолютная вел-на ее отклонения от мат ожид не превосходит утроенного среднего квадратического отклонения.

16 если СВ Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

17 Эмпирическим на-ют распределение относи­тельных частот. Эмпирические распределения изучает математическая статистика.

18Теоретическим на-ют распределение вероятностей. Теоретические распределения изучает теория вероятностей.

19 Асимметрией на-ют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения :

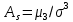
20Эксцессом на-ют хар-ку, которая опр-тся равенством

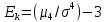
21Если каждому возможному знач случ-ой вел-ы Х соответствует одно возможное знач случ вел-ы У, то У на-ют ф-ей случ-ого аргум-та Х: Y =

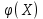
22а) Если различным возможным знач-ям аргумента Х соответ различные возможные знач ф-ии У, то вер-ти соответ знач Х и У между собой равны.

б) Если различ возмож знач Х соответ знач У, среди которых есть равные между собой, то следует складывать вер-и повторяющихся значений У.

---

23

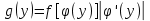
24Лусть аргумент Х -дискретная случ вел-на с возможными значениями х1 , х2, ••• , хп, вер-и которых соответственно равны р1, р2, • •• , Рп· Очевидно, У - также дискретная СВс возможными значениями у1 = 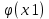y2 = 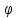(х2), ••• , Уп = 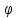(хп). Так как событие «величина Х приняла значение Х;» Влечет за собой событие «величина У приняла значение 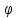(х;)», то вероятности возможных значений У соответственно равны р1, р2 , ••• , Рп · Сдедовательно, математическое ожидание функции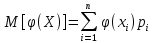

Пусть аргумент Х - непрерывная случайная величин а, заданная плотностью распределения f (х). Для отыскания мат ожидфункции У = 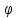(Х) можно сначала найти плотность распределения g (у) вел-ы У, а затем воспользоваться формулой или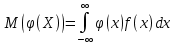
25Показательным (экспоненциальным) на-ют распределение вероятностей непрерывной случайной вел-ы Х. которое описывается плотностью 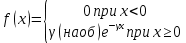где - постоянная положительная величина

26

27Показательным законом надежности на-ют функцию надежности, определяемую равенством

R (t) =е^-лt , где Л-интенсивность отказов.

---

Смотрите также файлы

• Рубежный контроль к разделу 2 по дисциплине Методология научных исследований.docx

• Информационные технологии работы с графикой.docx

• Наименование организации образования Сведения.docx

• Протокол 4 утверждаю Дополнительная общеразвивающая программа художественной направленности.doc

• Отчет по производственной практике (профилю специальности).docx