Файл: Задача 1 Определить собственные значения и собственные векторы матрицы третьего порядка. Решение.docx
Добавлен: 18.10.2024
Просмотров: 10
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
РАЗДЕЛ № 1. ЛИНЕЙНАЯ АЛГЕБРА
Задача 1
Определить собственные значения и собственные векторы матрицы третьего порядка.
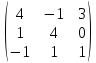
Решение:
Найдем собственные числа из характеристического уравнения:
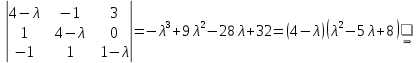
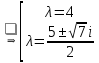
Для
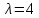 найдем его собственный вектор:
найдем его собственный вектор: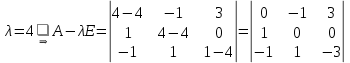
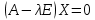
Тогда имеем однородную систему линейных уравнений.
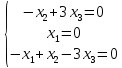
Решим ее методом Гаусса:
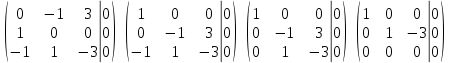
Тогда:
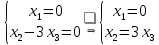
Собственный вектор:
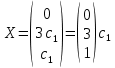
Задача 2
Доказать совместность системы и решить её тремя способами: по формулам Крамера, методом Гаусса и средствами матричного исчисления.
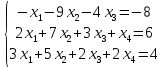
Решение:
Дана неоднородная система из трех линейных уравнений с четырьмя неизвестными. Для того чтобы исследовать систему, вычислим ранги основной и расширенной матриц данной системы уравнений, для чего приведём расширенную (а вместе с тем и основную) матрицу системы к ступенчатому виду:
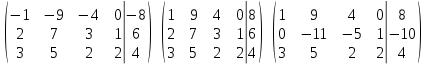
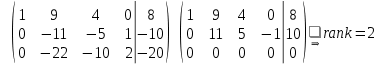
По теореме Кронекеля-Капелли ранг основной матрицы равен рангу расширенной матрицы и меньше количества переменных, значит система является совместной и неопределенной, т.е. имеет бесконечное множество решений.
Т.к. система является совместной и неопределенной, то методами Крамера и обратной матрицы ее решить невозможно.
Решим систему методом Гаусса:
Базисный минор
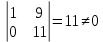
Базисные неизвестные
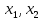 . Свободные неизвестные
. Свободные неизвестные 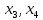 .
.Запишем укороченную систему:
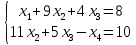
Полагаем, что
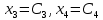 .
.Тогда:
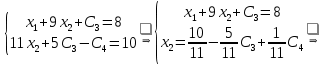
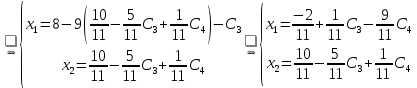
Общее решение системы:
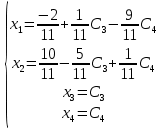
Задача 3
Исследовать и найти общее решение системы линейных однородных уравнений.
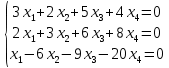
Решение:
Дана однородная система из трех линейных уравнений с четырьмя неизвестными. Для того чтобы исследовать систему, вычислим ранг матрицы данной системы уравнений, для чего приведём системы к ступенчатому виду:
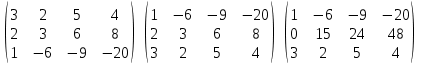
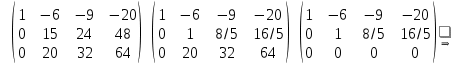
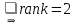
По теореме Кронекеля-Капелли ранг основной матрицы меньше количества переменных, значит система является совместной и неопределенной, т.е. имеет бесконечное множество решений.
Базисный минор
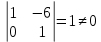
Базисные неизвестные
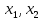 . Свободные неизвестные
. Свободные неизвестные 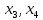 .
.Запишем укороченную систему:
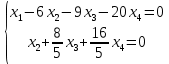
Полагаем, что
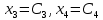 .
.Тогда:
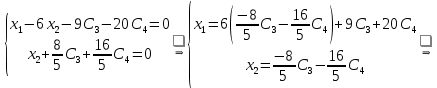
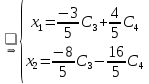
Общее решение системы:
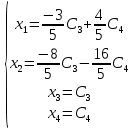
РАЗДЕЛ № 2. ВЕКТОРНАЯ АЛГЕБРА
Задача 1
Составить уравнение плоскости
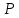 , проходящей через точку
, проходящей через точку 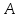
перпендикулярно вектору
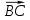 . Написать ее общее уравнение, а также нормальное уравнение плоскости и уравнение плоскости в отрезках. Составить уравнение плоскости
. Написать ее общее уравнение, а также нормальное уравнение плоскости и уравнение плоскости в отрезках. Составить уравнение плоскости 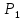 , проходящей через точки
, проходящей через точки 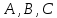 . Найти угол между плоскостями
. Найти угол между плоскостями  и
и 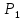 . Найти расстояние от точки
. Найти расстояние от точки 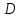 до плоскости
до плоскости  .
.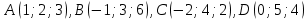
Решение:
1) Составить уравнение плоскости
 , проходящей через точку
, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору 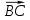 .
.Найдём координаты вектора
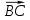 :
: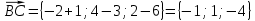
Запишем уравнение плоскости, проходящей через данную точку
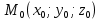 перпендикулярно данному вектору
перпендикулярно данному вектору 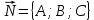 :
: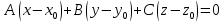
Подставляем координаты точки
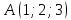 и координаты вектора
и координаты вектора 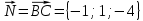 в уравнение
в уравнение 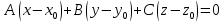 .
.Получаем:
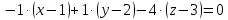
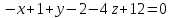
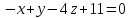
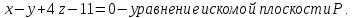
2) Написать ее общее уравнение, а также нормальное уравнение плоскости и уравнение плоскости в отрезках.
Общее уравнение плоскости
 :
: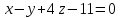
Нормальное уравнение плоскости
 :
: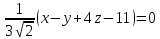
Уравнение плоскости
 в отрезках:
в отрезках: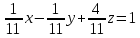
3) Составить уравнение плоскости
 , проходящей через точки
, проходящей через точки  .
.Запишем уравнение плоскости
 , проходящей через три заданные точки
, проходящей через три заданные точки 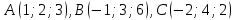 :
:Получаем:
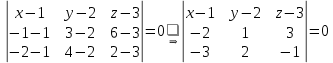
Вычислим определитель, разлагая его по первой строке:
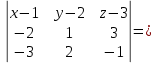
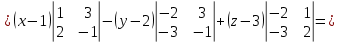
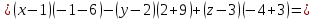
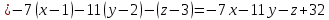
Следовательно, уравнение плоскости
 имеет вид:
имеет вид: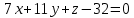
4) Найти угол между плоскостями
 и
и  .
.Угол между плоскостями равен углу между их нормальными векторами и вычисляется по формуле:
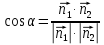
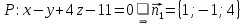
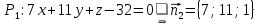
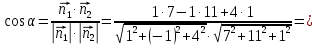
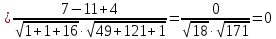
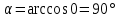
5) Найти расстояние от точки
 до плоскости
до плоскости  .
.Расстояние от точки
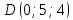 до плоскости
до плоскости 
, найдем по формуле:
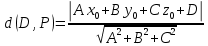
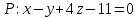
Тогда:
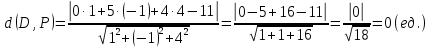
Задача 2
Прямая
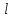 задана в пространстве общими уравнениями. Написать её каноническое и параметрическое уравнения. Составить уравнение прямой
задана в пространстве общими уравнениями. Написать её каноническое и параметрическое уравнения. Составить уравнение прямой 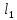 , проходящей через точку
, проходящей через точку 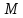 параллельно прямой
параллельно прямой 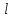 , и вычислить расстояние между ними. Найти проекцию точки
, и вычислить расстояние между ними. Найти проекцию точки 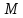 на прямую
на прямую 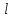 и точку пересечения прямой
и точку пересечения прямой 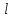 и плоскости
и плоскости  .
.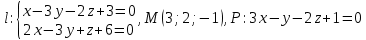
Решение:
1) Написать ее каноническое и параметрическое уравнения.
Чтобы записать канонические или параметрические уравнения прямой
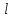 , необходимо знать координаты точки на прямой и координаты направляющего вектора этой прямой.
, необходимо знать координаты точки на прямой и координаты направляющего вектора этой прямой.По условию задачи прямая задана как линия пересечения двух плоскостей
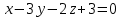 и
и 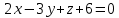 .
.По общим уравнениям этих плоскостей можно записать их векторы нормалей:
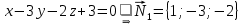
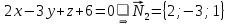
Векторы нормалей
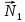 и
и 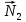 перпендикулярны искомой прямой, образованной пересечением плоскостей. Следовательно, её направляющий вектор может быть найден как векторное произведение векторов
перпендикулярны искомой прямой, образованной пересечением плоскостей. Следовательно, её направляющий вектор может быть найден как векторное произведение векторов 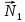 и
и 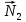 :
: