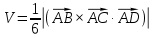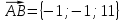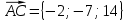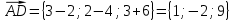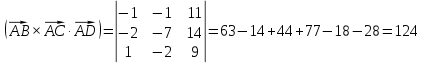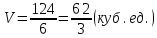Файл: Задача 1 Определить собственные значения и собственные векторы матрицы третьего порядка. Решение.docx
Добавлен: 18.10.2024
Просмотров: 11
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
пересечения прямых 
и 
:
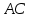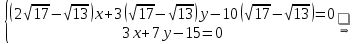
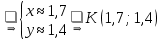
Тогда длина биссектрисы:
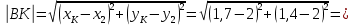
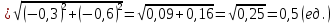
4) общее уравнение медианы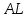
;
Для определения уравнения медианы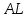 найдем координаты точки 
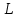, которая делит отрезок 
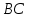пополам:
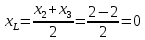
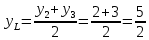
Тогда координаты точки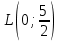
.
Медиана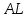 проходит через точк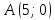и 
и .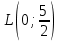
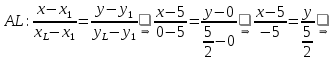
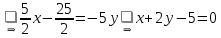
Длина медианы:
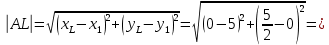
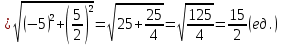
5) уравнения прямых, проходящих через вершины треугольника и параллельных его сторонам;
Чтобы составить уравнение прямой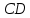
, найдем угловой коэффициент этой прямой. Так как 
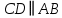, то угловые коэффициенты этих прямых равны между собой, т.е. 
.
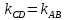Из уравнения стороны
.
Тогда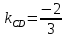
.
Составим уравнение прямой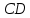 , зная угловой коэффициент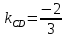
и координаты точки
:
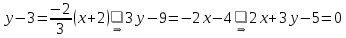
Чтобы составить уравнение прямой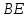
, найдем угловой коэффициент этой прямой. Так как 
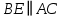, то угловые коэффициенты этих прямых равны между собой, т.е. 
.
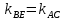Из уравнения стороны
.
Тогда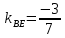
.
Составим уравнение прямой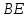 , зная угловой коэффициент 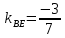и координаты точки 
:
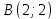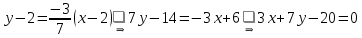
Чтобы составить уравнение прямой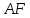
, найдем угловой коэффициент этой прямой. Так как 
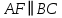, то угловые коэффициенты этих прямых равны между собой, т.е. 
.
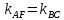Из уравнения стороны
.
Тогда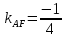
.
Составим уравнение прямой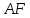 , зная угловой коэффициент 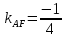и координаты точки 
:
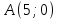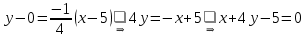
Сделаем рисунок:
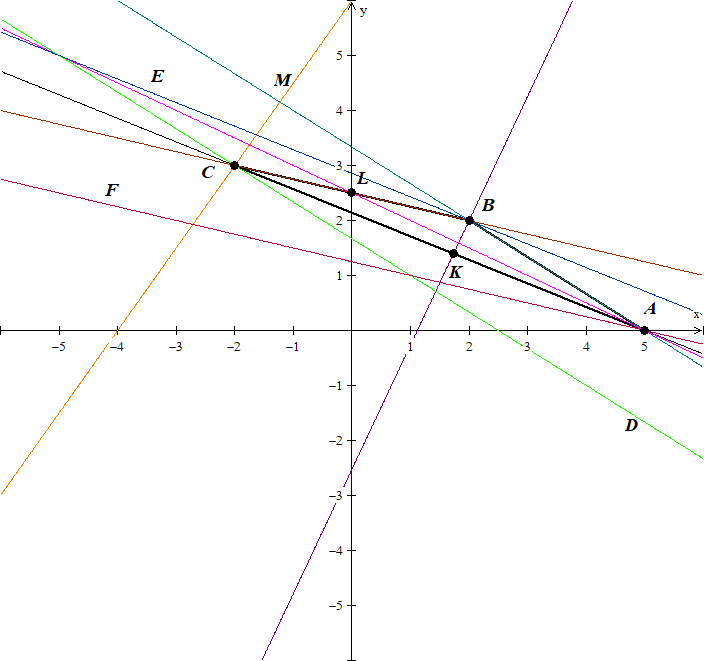
Задача 2
По координатам вершин пирамиды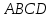
средствами векторной алгебры найти:
1) длины ребер
и 
;
2) угол между ребрами
и ;
3) площадь грани
;
4) проекцию вектор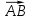а
на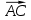 
;
5) объем пирамиды.
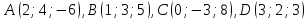
Решение:
1) длины ребер и ;
Длина ребра равна модулю вектора .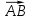
Модуль вектора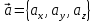
вычисляется по формуле:
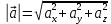
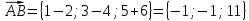
Подставляя в эту формулу исходные данные, получим:
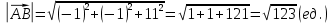
Длина ребра равна модулю вектора .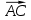
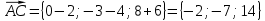
Подставляя в эту формулу исходные данные, получим:
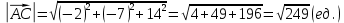
2) угол между ребрами и ;
Угол между ребрами и будем искать, используя формулу скалярного произведения векторов:
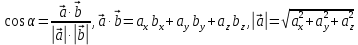
В нашем случае:
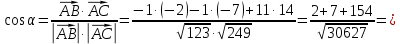
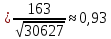
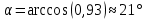
3) площадь грани ;
Площадь грани найдем как половину площади параллелограмма
, построенного на векторах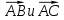
.
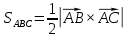
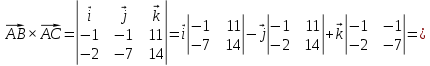
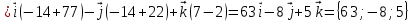
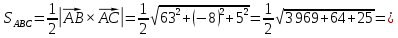
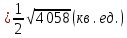
4) проекцию вектора на ;
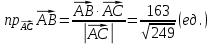
5) объем пирамиды.
Объем пирамиды
вычислим с помощью смешанного произведения трех векторов, на которых построена пирамида:
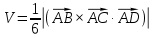
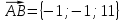
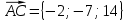
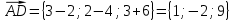
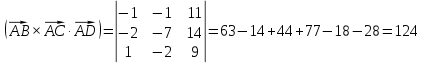
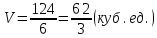
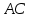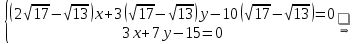
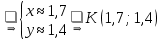
и : Тогда длина биссектрисы:
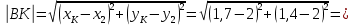
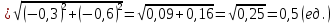
4) общее уравнение медианы
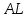;Для определения уравнения медианы
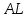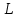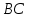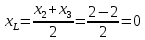
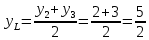
найдем координаты точки , которая делит отрезок пополам: Тогда координаты точки
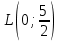.Медиана
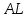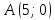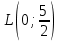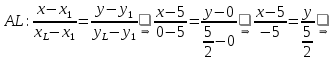
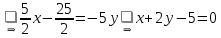
проходит через точки и . Длина медианы:
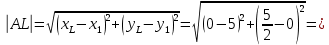
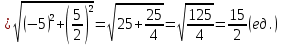
5) уравнения прямых, проходящих через вершины треугольника и параллельных его сторонам;
Чтобы составить уравнение прямой
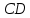, найдем угловой коэффициент этой прямой. Так как 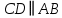, то угловые коэффициенты этих прямых равны между собой, т.е. 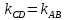.Из уравнения стороны
.Тогда
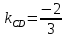.Составим уравнение прямой
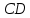, зная угловой коэффициент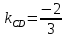
и координаты точки
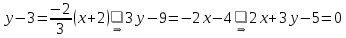
: Чтобы составить уравнение прямой
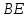, найдем угловой коэффициент этой прямой. Так как 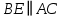, то угловые коэффициенты этих прямых равны между собой, т.е. 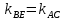.Из уравнения стороны
.Тогда
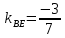.Составим уравнение прямой
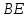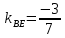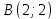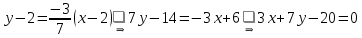
, зная угловой коэффициент и координаты точки : Чтобы составить уравнение прямой
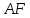, найдем угловой коэффициент этой прямой. Так как 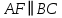, то угловые коэффициенты этих прямых равны между собой, т.е. 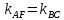.Из уравнения стороны
.Тогда
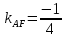.Составим уравнение прямой
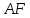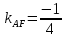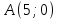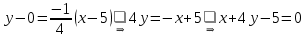
, зная угловой коэффициент и координаты точки : Сделаем рисунок:
Задача 2
По координатам вершин пирамиды
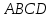средствами векторной алгебры найти: 1) длины ребер
и ; 2) угол между ребрами
и
; 3) площадь грани
; 4) проекцию вектора
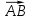на 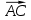; 5) объем пирамиды.
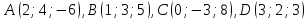
Решение:
1) длины ребер
и ; Длина ребра
равна модулю вектора 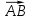. Модуль вектора
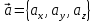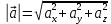
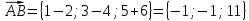
вычисляется по формуле: Подставляя в эту формулу исходные данные, получим:
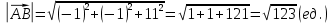
Длина ребра
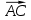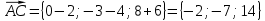
равна модулю вектора . Подставляя в эту формулу исходные данные, получим:
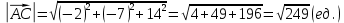
2) угол между ребрами
и ;Угол между ребрами
и будем искать, используя формулу скалярного произведения векторов: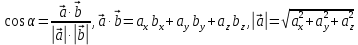 В нашем случае:
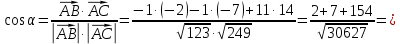
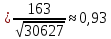
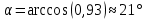
3) площадь грани
; Площадь грани
найдем как половину площади параллелограмма
, построенного на векторах
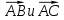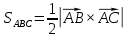
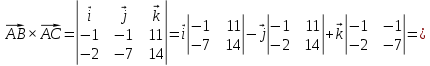
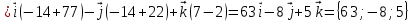
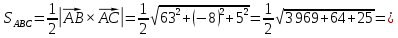
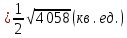
. 4) проекцию вектора
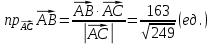
на ; 5) объем пирамиды.
Объем пирамиды
вычислим с помощью смешанного произведения трех векторов, на которых построена пирамида: