Файл: Задача 1 Определить собственные значения и собственные векторы матрицы третьего порядка. Решение.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Решение задач

Дисциплина: Не указана

Добавлен: 18.10.2024

Просмотров: 12

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.




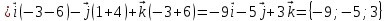
Определим точку, лежащую на прямой. Для этого решим систему уравнений:



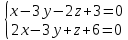
При 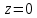получаем: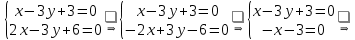





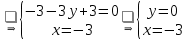
Таким образом, точка, лежащая на данной прямой, имеет координаты .

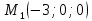Записываем канонические уравнения прямой :



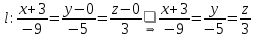
и параметрические уравнения:


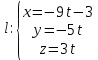
2) Составить уравнение прямой , проходящей через точку параллельно прямой , вычислить расстояние между ними.

Чтобы составить уравнение прямой , проходящей через точку , параллельно прямой , в качестве направляющего вектора искомой прямой возьмем направляющий вектор прямой :



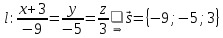
В то же время прямая проходит через точку 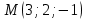, значит ее уравнение имеет вид: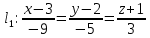



Найдем расстояние между прямыми и .

Расстояние от точки до прямой будем рассматривать как длину высоты параллелограмма, построенного на векторах 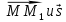, где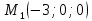
– точка на прямой , 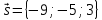– направляющий вектор прямой .



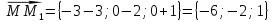
Тогда:



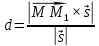
Находим векторное произведение:





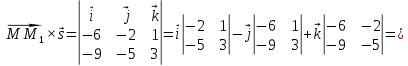
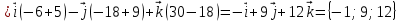
Находим модули векторов:





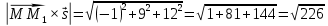
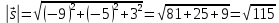
Подставляя найденные значения в формулу, находим расстояние от точки до прямой: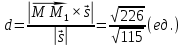


3) Найти проекцию точки на прямую и точку пересечения прямой и плоскости .

Найдем проекцию точки на прямую .

Найдем уравнение плоскости, которая перпендикулярна к прямой и проходит через точку .

Для этого нам нужно знать координаты нормального вектора плоскости.

Направляющий вектор прямой является нормальным вектором плоскости, которая перпендикулярна к прямой . То есть, 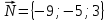– нормальный вектор плоскости. Тогда уравнение плоскости 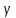, проходящей через точку и имеющей нормальный вектор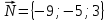
, имеет вид:





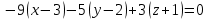
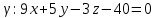
Осталось найти координаты точки пересечения прямой и плоскости – они являются искомыми координатами проекции точки на прямую .

Подставим в уравнение плоскости вместо 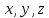их выражения через параметр:



Теперь мы можем вычислить искомые координаты точки пересечения прямой 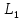и плоскости по параметрическим уравнениям прямой: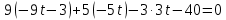





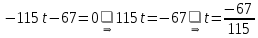
Таким образом, проекция точки на прямую имеет координаты:



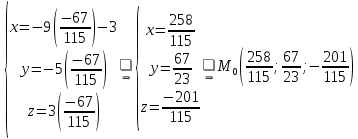
Найдем точку пересечения прямой и плоскости .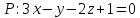

Запишем уравнение прямой в параметрическом виде:



Подставим значения 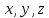в уравнение плоскости :





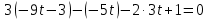
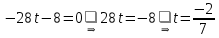
Теперь найдем значения координат 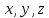, соответствующие параметру :



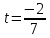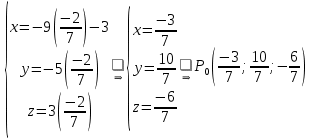
Точка пересечения прямой и плоскости .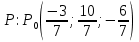

РАЗДЕЛ № 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Задача 1

Даны координаты вершин треугольника . Составить уравнения сторон треугольника. Составить уравнения медианы, высоты и биссектрисы угла , найти их длины. Составить уравнения прямых, проходящих через вершины треугольника и параллельных его сторонам.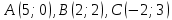



Решение:

1) общие уравнения всех сторон треугольника;

Уравнения сторон 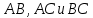найдем по формуле уравнения прямой, проходящей через две точки: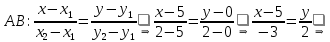





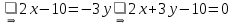
Из уравнения стороны .





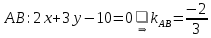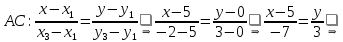
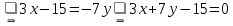
Из уравнения стороны .





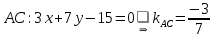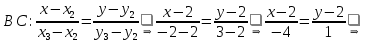
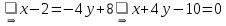
Из уравнения стороны .
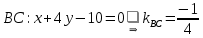2) общее уравнение высоты ;

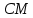Для составления уравнения высоты 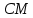, воспользуемся условием перпендикулярности прямых: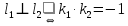



Так как 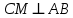, то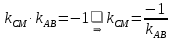

Так как 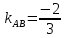, то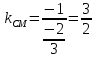

Уравнение прямой с угловым коэффициентом
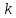
, проходящей через точку 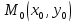, имеет вид: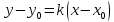



Тогда уравнение высоты 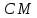с угловым коэффициентом 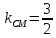, проходящей через точку 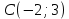, имеет вид: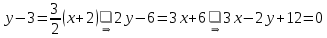



Чтобы найти длину высоты, найдем расстояние от точки 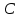до прямой 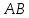, воспользуемся формулой расстояния от точки до прямой: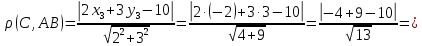




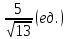
3) общее уравнение биссектрисы ;

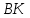Найдем уравнение биссектрисы угла .

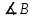Приведем уравнения сторон 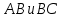к нормальному виду: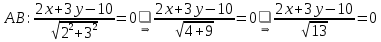





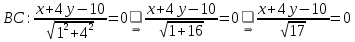
Биссектриса угла между двумя прямыми есть геометрическое место точек, равноудаленных от сторон угла.

Тогда уравнения биссектрис между прямыми :















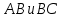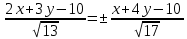
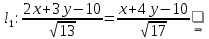
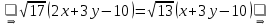
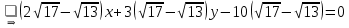
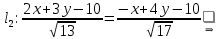
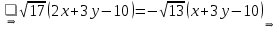
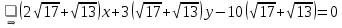
Уравнение биссектрисы :



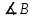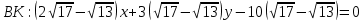
Чтобы найти длину биссектрисы, найдем точку

Смотрите также файлы