Рубцова
Задание. Для функции ???? = (2???? + 3)???? 5????

1. Найти область определения, точки разрыва. 

2. Исследовать функцию на четность, периодичность. 

3. Исследовать поведение функции на концах области определения. Указать асимптоты. 

4. Найти промежутки монотонности. Точки экстремума.

5. Найти промежутки выпуклости. Точки перегиба. 

6. Найти площадь фигуры, ограниченной графиком функции ???? = (2???? + 3)???? 5???? и прямыми ???? = 0, ???? = 2, ???? = 0. Результаты исследования оформить в виде таблицы.
.

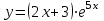1) Область определения функции: .

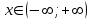2) Точек разрыва нет.

3) Так как 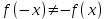и 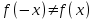, то функция является ни четной и нечетной, график данной функции имеет общий характер.

4) Функция непериодическая.

5) Найдем точки экстремума и интервалы монотонности

Для этого найдем первую производную от заданной функции и приравняем ее к нулю.



.

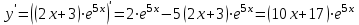
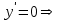
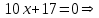
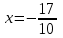Снесем данные в таблицу:

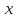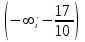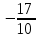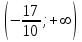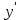	-	0	+
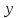	убывает	1	возрастает

При

---

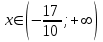- возрастает. При 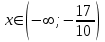- убывает.

- точка минимума.
6) Найдем точки перегиба и интервалы выпуклости и вогнутости.

Для этого найдем вторую производную от заданной функции и приравняем ее к нулю



.

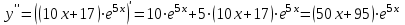
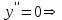
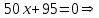
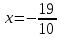Снесем данные в таблицу:

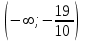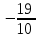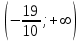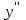	-	0	+
	выпуклый		вогнутый

При 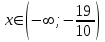график функции выпуклый, при 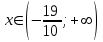- график функции вогнутый.

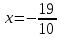- точка перегиба.
7) Найдем наклонные асимптоты

Исследуем при .



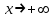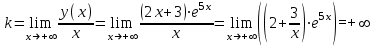
При 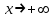горизонтальных и наклонных асимптот нет.
Исследуем при .





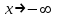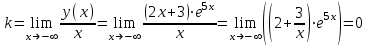
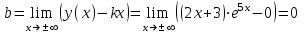
Следовательно, при

---

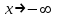
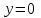, - горизонтальная асимптота, наклонных асимптот нет.

8) Найдем точки пересечения с координатными осями:

.

.

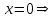
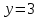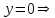
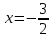9) Построим график



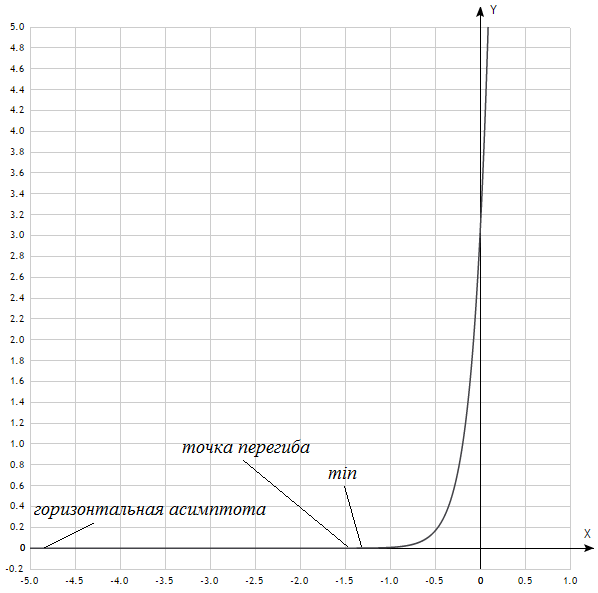
10) Используя свойства определенного интеграла, искомая площадь будет равна:

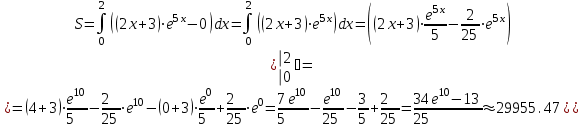(условных квадратных единиц).
Снесем полученные результаты в таблицу:

Область определения:
Четность, периодичность:	Функция является ни четной и нечетной, не периодичная
Поведение на концах области определения:	При 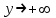При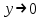
Асимптоты:	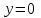- горизонтальная асимптота
Промежутки монотонности:	При график функции выпуклый, при - график функции вогнутый.
Точки экстремума:	- точка минимума
Промежутки выпуклости:	При график функции выпуклый, при - график функции вогнутый.
Точки перегиба:	- точка перегиба
Площадь криволинейной трапеции:	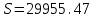условных квадратных единиц.

---

---

Смотрите также файлы

• 1. Введение в деловое общение Задание 1.docx

• Фамилия, имя 6 класс Дата 1.doc

• .rtf

• .rtf

• Расчетнографическая работа по дисциплине механика.docx