Добавлен: 18.10.2024
Просмотров: 23
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Определение реакций связей для двухопорной балки
Определение реакций связей для консольной балки
Определение траектории, скорости и ускорения точки по заданным уравнениям ее движения
Кинематический анализ механической системы при плоском движении
Применение теоремы об изменении кинетической энергии к изучению движения механической системы
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное
образовательное учреждение высшего образования
«Уфимский государственный авиационный технический университет»
| | Кафедра сопротивления материалов |
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
по дисциплине «МЕХАНИКА»
Семестр 4
| Выполнил студент группы ПБ-219з | А. И. Алексеев |
| | |
| Принял профессор кафедры сопротивления материалов | В. П. Павлов |
Уфа 2022
Оглавление
Задача 1. 3
Определение реакций связей для двухопорной балки 3
Задача 2. 7
Определение реакций связей для консольной балки 7
Задача 3. 11
Определение траектории, скорости и ускорения точки по заданным уравнениям ее движения 11
Задача 4. 16
Кинематический анализ механической системы при плоском движении 16
Задача 5. 21
Применение теоремы об изменении кинетической энергии к изучению движения механической системы 21
Задача 1.
Определение реакций связей для двухопорной балки
1.1. Задание на расчет
Определить реакции наложенных на балку внешних связей. Форма и размеры балки с приложенными к ней внешними нагрузками представлены на рис. 1.1.
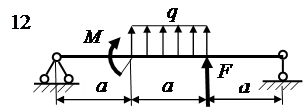
| Рис. 1.1. Прямая балка, ее размеры, наложенные на нее связи и действующие на нее нагрузки |
Исходные данные
Задана прямая балка, нагруженная силой
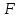
, парой сил с моментом
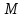 и равномерно распределенной нагрузкой интенсивностью
и равномерно распределенной нагрузкой интенсивностью 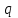 (рис. 1.1). Балка имеет две опоры (внешние связи): неподвижный цилиндрический шарнир (в точке
(рис. 1.1). Балка имеет две опоры (внешние связи): неподвижный цилиндрический шарнир (в точке 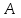 ) и подвижный цилиндрический шарнир (в точке
) и подвижный цилиндрический шарнир (в точке 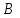 ). Размеры балки показаны на рис. 1.2.
). Размеры балки показаны на рис. 1.2.Расчеты выполнить при исходных данных, заданных в табл. 1.1
Таблица 1.1
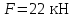 | 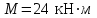 | 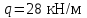 | 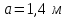 |
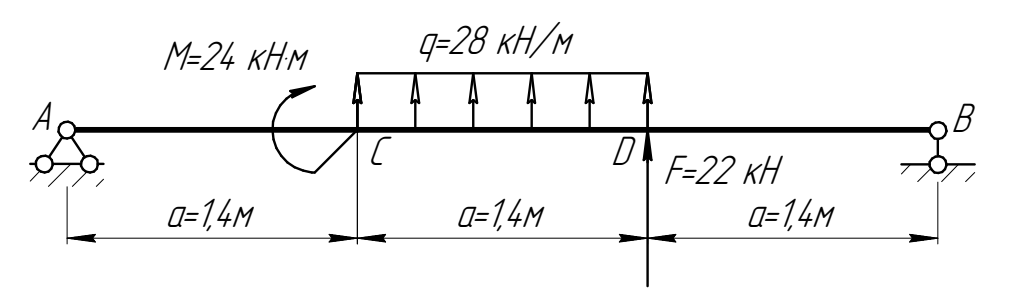
Рис. 1.2. Прямая балка, ее размеры, наложенные на нее связи и действующие на нее нагрузки (числовые данные)
1.2. Определение реакций внешних связей
Для определения опорных реакций (реакций наложенных на балку внешних связей), изобразим в масштабе на рис. 1.2 соответствующую расчетную схему и выполним следующие необходимые действия.
1. Для исключения ошибок, связанных с размерностями рассматриваемых в расчетах величин, необходимо согласно системе СИ:
-
размеры измерять в метрах (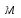 );
); -
силы измерять в ньютонах (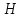 );
); -
моменты пар сил измерять в ньютон-метрах (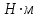 );
); -
интенсивности распределенной нагрузки измерять в ньютонах, приходящихся на один метр (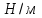 ).
).
В итоге запишем:
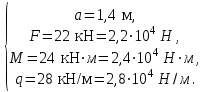 | (1.0) |
2. Изобразим балку и связанные с ней оси
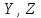 правой декартовой системы координат
правой декартовой системы координат 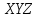 (рис. 1.3).
(рис. 1.3).3. Заменим равномерно распределенную нагрузку
 , действующую на участке
, действующую на участке 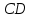 , ее равнодействующей
, ее равнодействующей 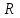 , модуль которой определяется как площадь фигуры (прямоугольника), изображающей на рис. 1.2 распределённую нагрузку
, модуль которой определяется как площадь фигуры (прямоугольника), изображающей на рис. 1.2 распределённую нагрузку  :
: 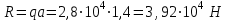 . . | (1.0) |
Сила
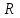 направляется в ту же сторону, что и распределенные силы
направляется в ту же сторону, что и распределенные силы  , а линия действия силы
, а линия действия силы 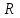 проходит через центр тяжести фигуры (прямоугольника), изображающей распределённую нагрузку
проходит через центр тяжести фигуры (прямоугольника), изображающей распределённую нагрузку  . В итоге на рис. 1.3 показана сила
. В итоге на рис. 1.3 показана сила 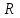 , заменяющая распределенную нагрузку
, заменяющая распределенную нагрузку  , и задано расстояние (
, и задано расстояние (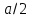 ) от точки
) от точки 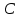 до линии действия силы
до линии действия силы 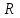 .
.4. Приложим к балке все внешние задаваемые силы
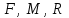 (рис. 1.3).
(рис. 1.3).5. Согласно принципу освобождаемости тел от связей отбросим мысленно внешние связи (шарниры на рис. 1.2) и заменим их соответствующими реакциями связей (рис. 1.3).
В точке
 связью является неподвижный цилиндрический шарнир, действие которого заключается в создании двух реакций:
связью является неподвижный цилиндрический шарнир, действие которого заключается в создании двух реакций:-
силы-реакции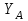 , направленной вдоль оси
, направленной вдоль оси 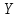 ;
; -
силы-реакции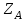 , направленной вдоль оси
, направленной вдоль оси 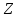 .
.
В точке
 связью является подвижный цилиндрический шарнир, действие которого заключается в создании одной силы-реакции
связью является подвижный цилиндрический шарнир, действие которого заключается в создании одной силы-реакции 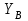 , направленной вдоль оси
, направленной вдоль оси  .
.На расчетной схеме силы-реакции
 ,
,  ,
, 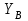 направляем в сторону направления соответствующих координатных осей
направляем в сторону направления соответствующих координатных осей  (рис. 1.3).
(рис. 1.3).Таким образом, нам необходимо определить три неизвестных реакций связей
(
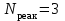 ):
):  ,
,  ,
, 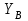 (рис. 1.3).
(рис. 1.3). 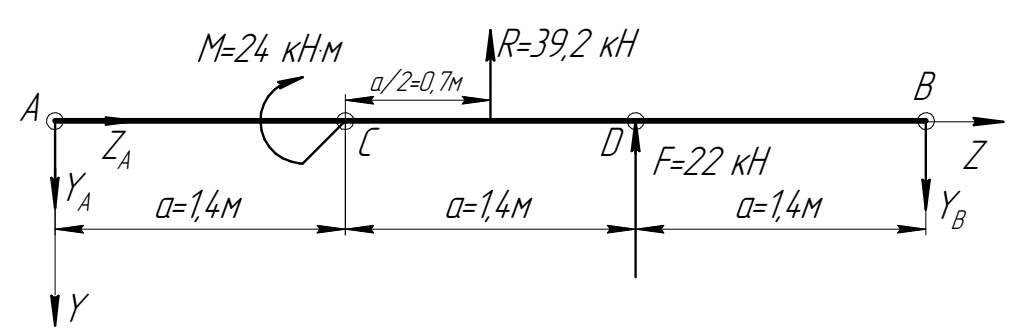 |
| Рис. 1.3. Расчетная схема балки при определении опорных реакций |
6. Записываем для изображенной на рис. 1.3 плоской системы сил три уравнения равновесия (
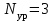 ):
): 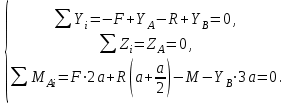 | (1.0) |
Число уравнений равновесия в системе (1.0).равно числу неизвестных реакций
(
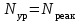 ). Из этого следует, что все неизвестные реакции можно определить из уравнений равновесия. В этом случае говорят, что балка статически определима.
). Из этого следует, что все неизвестные реакции можно определить из уравнений равновесия. В этом случае говорят, что балка статически определима.Подставим в систему уравнений (1.0) заданные силы, момент пары сил и заданные размеры и после ряда преобразований и вычислений придем к системе уравнений:
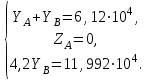 | (1.0) |
Из (1.0) получим
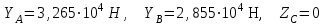 . . | (1.0) |
Знак плюс у значений сил
 и
и  указывает на то, что действительное направление этой силы совпадает с изображенным на рис. 1.3.
указывает на то, что действительное направление этой силы совпадает с изображенным на рис. 1.3.7. Для проверки правильности расчетов запишем уравнение равновесия моментов относительно любой другой точки, за исключением ранее использованной точки
 .
.Затем на рис. 1.4 выберем за полюс какую-либо точку (например, точку
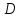 ) и проверим, как в этом случае соблюдается уравнение равновесия моментов:
) и проверим, как в этом случае соблюдается уравнение равновесия моментов: 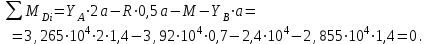 | (1.0) |
Равенство нулю суммы моментов всех сил относительно точки
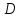 подтверждает правильность найденных значений реакций связей
подтверждает правильность найденных значений реакций связей  ,
,  ,
,  .
.