Файл: Статистический анализ и планирование эксперимента.docx

Министерство науки и высшего образования Российской Федерации

ФГБОУ ВПО

«Иркутский государственный технический университет»
Институт недропользования
Кафедра Нефтегазового дела


СТАТИСТИЧЕСКИЙ АНАЛИЗ И ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
Макет отчета по контрольной работе

для обучающихся по заочно форме обучения

Иркутск

2019 г.
ВВЕДЕНИЕ
Настоящий макет предназначен для помощи обучающимся по программе дисциплины «Статистический анализ и планирование эксперимента» при выполнении контрольной работы.

Данный мает применяется следующим образом.

Текст макета принимается за основу.

В свободные места текста, обозначенные различным образом, необходимо внести результаты выполнения контрольной работы в соответствии с индивидуальным заданием.
1 СТАТИСТИЧЕСКИЙ АНАЛИЗ СЛУЧАЙНЫХ ВЕЛИЧИН
1.1. Статистический анализ одномерной последовательности случайных величин
Цель работы: приобрести компетенции статистического анализа одномерной последовательности случайных величин.
Задание:

1. 
   Подготовить исходные данные.
   
2. 
   Построить вариационный, статистический, группированный ряды.
   
3. 
   Построить гистограмму, полигон, кумуляту, огиву.
   
4. 
   Определить относительные частоты последовательности.
   
5. 
   Определить: среднее арифметическое (по вариационному ряду), средневзвешенное (по группированному ряду), моду, медиану, дисперсию (по группированному ряду); среднее квадратическое отклонение , коэффициент вариации.
   
6. 
   Рассчитать в программе Excel характеристики описательной статистики для заданной последовательности случайных величин.
   

1. 
   Исходные данные
   

В качестве исходных данных принята (назначить самостоятельно числовые характеристики из нефтегазовой сферы или в соответствии с вариантом задания, которые приведены в файле с заданиями) (табл. 1.1).
Таблица 1.1- Наименование случайной величины, е.и.

75	35	4	91	73	35	9,9	44	38	22
40	91,3	84,5	80	75	35	4	91	73	35
9,9	44	38	22	40	91,3	84,5	80	75	35
4	91	73	35	9,9	44	38	22	40	91,3
84,5	80	75	35	4	91	73	35	9,9	44

---

Средствами программы Excel рассчитаны характеристики описательной статистики заданной последовательности значений случайной величины (в качестве исходных данных необходимо применять данные таблицы 1.1), числовые значения которых приведены на рисунке 1.1.


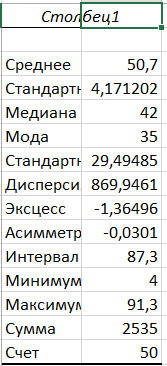
Рисунок 1.1 – Характеристики описательной статистики случайной величины

2. 
   Вариационный ряд
   

Вариационный ряд – последовательность, записанная в возрастающем порядке.

Для заданной последовательности случайных величин вариационный ряд показан в таблице 1.2.
Таблица 1.2- Вариационный ряд

4	4	4	4	9,9	9,9	9,9	9,9	22	22
22	35	35	35	35	35	35	35	35	38
38	38	40	40	40	44	44	44	44	73
73	73	73	75	75	75	75	80	80	80
84,5	84,5	84,5	91	91	91	91	91,3	91,3	91,3

Характеристики вариационного ряда:

• 
  максимальное значение ряда Х_max = 91,3;
  
• 
  минимальное значение ряда X_min = 4;
  
• 
  размах ряда определяется по формуле:
  

R = X_max – X_min = 87,3.

3. 
   Характеристики статистических рядов
   

Статистический ряд - перечень вариант и соответствующих им частот или относительных частот. Могут быть:

группированными – например, группируются значения с одинаковыми величинами;

интервальными – группировка выполняется по количеству попаданий в интервал (дать определение и классификацию статистических рядов).

1. 
   Группированный статистический ряд
   

---

Группированный статистический ряд - совокупность середин интервалов (дать определение).

Группированный статистический ряд для заданных исходных данных приведен в табл. 1.3.

Таблица 1.3 - Группированный статистический ряд

_________Хi_______	__________ni________
4	4
9,9	4
22	3
35	8
38	3
40	3
44	4
73	4
75	4
80	3
84,5	3
91	4
91,3	3

Графическое представление статистических характеристик группированного ряда
Гистограмма для группированного ряда.

Гистограмма - представляет собой столбиковую диаграмму частот. (дать определение).

Гистограмма по заданным значениям группированного ряда показана на рисунке 1.2.



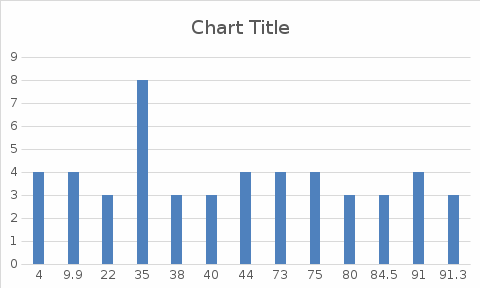
Рисунок 1.2 - Гистограмма для группированного ряда
Полигон для группированного ряда

Полигон – это ломаная, отрезки которой соединяют середины отрезков, образующих прямоугольники в гистограмме. (дать определение).

Полигон для группированного ряда показан на рисунке 1.3.


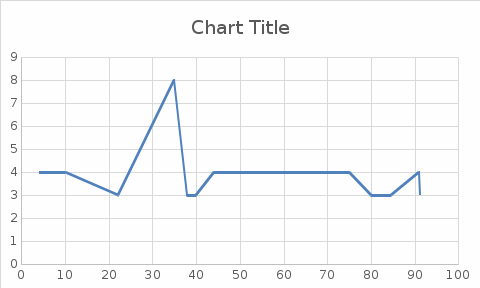
Рисунок 1.3 – Полигон для группированного ряда
Кумулята для группированного ряда.

Кумулята – служит для графического изображения кумулятивного вариационного ряда. (дать определение).

Кумулята для группированного показан на рисунке 1.4.


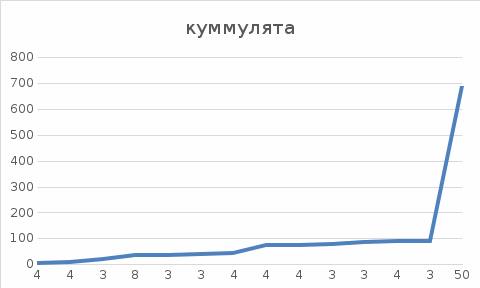
Рисунок 1.4 – Кумулята для группированного ряда
Огива для группированного ряда.

Огива – это обратная функция по отношению к кумуляте. (дать определение).

Огива для группированного ряда показана на рисунке 1.5.

---

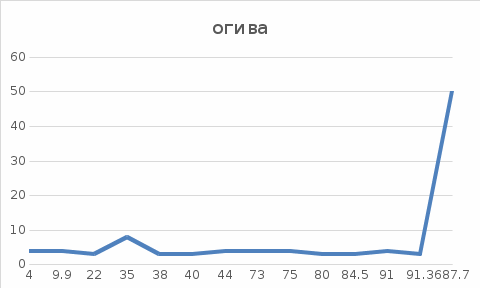
Рисунок 1.5 – Огива для группированного ряда
Статистические характеристики группированного ряда
Объем выборки группированного ряда.

Объем выборки – число случаев, включённых в выборочную совокупность. (дать определение).

Объём выборки определяется по формуле:
N= (g² * z²) / d²,
где: N – искомый объем выборки;

g – дисперсия признака, ожидаемое среднее отклонение получаемых результатов от ожидаемого среднего значения;

z – коэффициент уровня достоверности (2 – для 0,95, 3 – для 0,99);

d – уровень точности. (дать расшифровку всех обозначений в формулах, далее во всех формулах выполнят подобную расшифровку, как это предусмотрено в СТО ИРНИТУ 005-2020 и ГОСТ).
При заданных значениях ряда получим:
N= ___________________________.= _________,
Относительная частота.

Относительна частота - (дать определение).

Относительна частота определяется по формуле:
W = ,
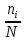где N – объе;

n_i (расшифровать).
Для первого значения ряда получим:
W = ,
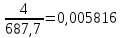Значения относительных частот приведены в таблице 1.4.
Таблица 1.4- Относительные частоты для группированного ряда

Частота повторений	Сумма n	Относительная частота W	Сумма относительной частоты
4	687,7	0,005816	1
9,9		0,014396
22		0,031991
35		0,050894
38		0,055257
40		0,058165
44		0,063981
73		0,106151
75		0,109059
80		0,11633
84,5		0,122873
91		0,132325
91,3		0,132761

Среднее арифметическое группированного ряда.

Среднее арифметическое ряда - (дать определение

---

).

Среднее арифметическое ряда определяется по формуле:
X_ср= __________,

где ???
Для заданных исходных данных получим:
X_св= ___________.
Средневзвешенное группированного ряда.

Средневзвешенное значение статистического ряда – (дать определение).

Средневзвешенное значение статистического ряда определяется по формуле:

X= ________,

где ????
Для заданных исходных данных получим:
X= ______________________ = _____,
Мода группированного ряда

Мода – (дать определение).

Мода для группированного ряда и для заданного ряда случайных величин имеет значение:
M = __________.
Медиана группированного ряда.

Медианой называется – (определение).
Медиана для группированного ряда рассчитывается по формуле:
Me = ______ ,
где ???????.

При заданных значениях получим:
Me = ______ ,
Дисперсия группированного ряда.

Дисперсия – (дать определение).

Дисперсия может быть рассчитана по формуле:
D =_________________,
где ?????.
Данные для расчета дисперсии для других групп ряда приведены в таблице 1.5.
Таблица 1.5 – Данные для расчета дисперсии ряда

Номер группировки ряда	Значения СВ, Хi	Частоты ni	Среднее арифметическое	(xi-xср)2*nt	1/(n-1)
1
2
3
4
…
…
…
…
…
…

Тогда дисперсия для группированного ряда определится так:
D = ______________________________________________.
Среднее квадратическое отклонение группированного ряда.

---