Файл: zapiska-1.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 22.10.2024

Просмотров: 8

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

3. ПРОЕКТИРОВАНИЕ И РАСЧЁТ ЗУБЧАТОЙ ПЕРЕДАЧИ

3.1 Геометрический расчет зубчатой передачи

Исходные данные:

  1. число зубьев шестерни z5=40;

  2. число зубьев колеса z6=132;

  3. модуль m=6 мм.

Нарезание проводится методом обкатки инструментом реечного типа, который профилируется на основе исходного контура по ГОСТ 13755-81 и имеет следующие параметры:

угол профиля α=20º;

коэффициент высоты головки ha*=1,

коэффициент радиального зазора С*=0.25.

Определяем геометрические параметры эвольвентной передачи:

1)Делительное межосевое расстояние:

а= 0.5*m(z5+ z6)=0.5*6(40+132)=516 мм;

2) Межосевое расстояние: aw=а=516 мм;

3) Минимальные коэффициенты смещения:

x5=(17- z5)/17=(17-40)/17=-1,88;

x6=1,88.

Т.к. коэффициент смещения х > 1, принимаем х = 0.

4) Угол профиля исходного контура; α=20º,

5) inva = inv20° = 0,0149;

6) Делительная высота головки зуба:

ha5= ha6=m*ha*=6*1 =6 мм;

7) Делительная высота ножки зуба:

hf5 = hf6 = m*(ha* + С* )= 6*(1+0.25)=7,5 мм;

8) Высота зуба:

h5=h6=m(2* ha*+ С*)=6*(2*1+0.25)=13,5 мм.

9) Делительные диаметры:

d5=m*z5=6*40=240 мм;

d6=m*z6=6*132=792 мм.

10) Основные диаметры:

db5=m*z5*cos α=6*40*0.9397=225,5 мм;

db6=m*z6*cos α=6*132*0.9397=744,2 мм.

11) Начальные диаметры:

dw5 = d5 = 240 мм;

dw6 = d6 = 792 мм.

12) Диаметры вершин зубьев:

da5 = m * z5 + 2*m*ha*=6*40+2*6*1= 252 мм;

da6 = m * z6 + 2*m*ha* =6*132+2*6*1= 804 мм.

13) Диаметры впадин зубьев:

df5 =m*z5 - 2*m*( ha* + c*) = 6*40 - 2*6(1+0.25)= 225 мм;

df6 = m*z6 - 2*m*( ha* + c*) = 6*132 - 2*6(1+0.25)= 777 мм.

14) Начальная толщина зубьев:

S5= S6 = 0.5*p*m + 2*m*tga = 0.5 * 3.14*6 + 2*6*0.3639=13,8 мм;

15) Делительный шаг зубьев:

Р=p * m = 3.14 * 6=18,8 мм.

16) Основной шаг зубьев:

Рb = p * m * сosa = 3.14 * 6 * 0.9397=17,7 мм.

17) Угол профиля по окружности вершин:

αа5= аrccos db5/da5= аrccos (225,5/252)= 26 º;

αа6= аrccos db6/da6= аrccos (744,2/804)=22º.

19) Радиус кривизны галтели:

r = 0.38 * m = 0.38 * 6=2,3 мм.

По полученным данным строим эвольвентное зацепление, масштабный

коэффициент построения принимаем Кl=0.001 м/мм.

Коэффициенты торцевого перекрытия:

εαа=( z5* tg αa5 + z6* tg αa6 –( z5 + z6)* tg α w)/2*p;

εαа =(40* tg 26º +132*tg22º -(40+132)*0.3639)/2*3.14=1,6 мм,

3.2 Синтез и анализ планетарного редуктора:

  1. Исходные данные:

  2. Частота вращения двигателя nдв=900 мин-1;

  3. Частота вращения кривошипа nкр= 75 мин-1;

  4. Число зубьев шестерни z5=40;

  5. Число зубьев колеса z6=132;

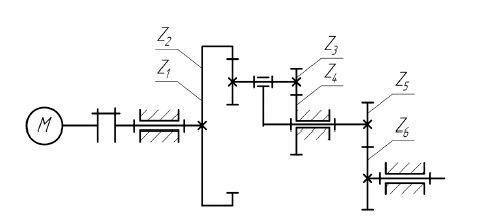
Рисунок 2 – Схема планетарного редуктора.

Общее передаточное отношение редуктора:

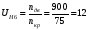
Передаточное отношение простой передачи z5-z6:

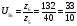
Передаточное отношение планетарной передачи:

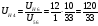
Формула Виллиса. Передаточное отношение обращённого механизма:

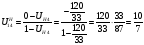
Передаточное отношение обращенного планетарного механизма, выраженное в числах зубьев:

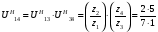
Условие соосности для данной передачи:

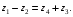
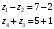
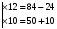
Принимаем числа зубьев колёс, равных: z1=84; z2=24; z3=10; z4=50. По принятым числам зубьев определяем диаметры колёс:

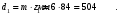
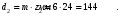
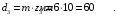
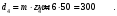
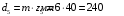
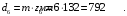
Принимаем масштабный коэффициент построения кинематической схемы редуктора:

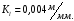
Скорость точки А зубчатого колеса 1:

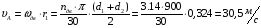
Строим планы скоростей. Масштабный коэффициент плана скоростей:

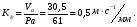
Для построения плана частот вращения выбираем масштабный коэффициент построений:

Kn=nдв/0-H=900/68=13 мин-1/мм/

Из плана частот имеем:

n2=(0-2)×Kn=170×13=2210 мин-1

n5=(0-5)×Kn=115×13=1496 мин-1

n6=(0-6)×Kn=25×13=325 мин-1

4. Синтез и анализ кулачкового механизма

Исходные данные:

1) Диаграмма движения выходного звена (.рис. 4.1)

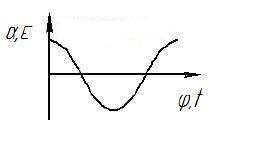
Рисунок 4.1 - диаграмма движения выходного звена

2) Частота вращения кулачка ;

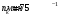3) Максимальный подъем толкателя ;

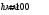4) Рабочий угол кулачка ;

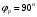5) Угол давления ;

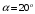6) Дезаксиал кулачка е = 40 мм;

7) Роликовый тип кулачкового механизма со смещением (рис 4.2).

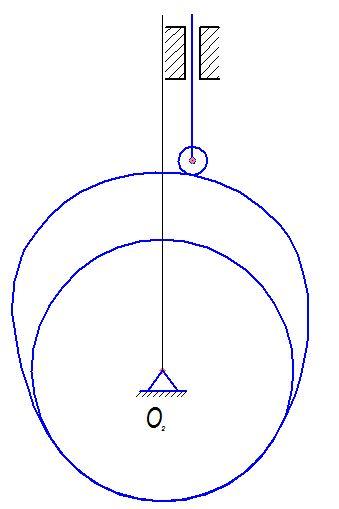
Рис. 4.2 - Роликовый тип кулачка со смещением

4.1. Диаграмма движения толкателя

По заданному графику ускорения толкателя а = f(t), графическим интегрированием по методу хорд получаю графики скорости и перемещения толкателя.

База интегрирования:

Графики V(s), a(s) получаю методом исключения общего переменного параметра t - время.

Масштабный коэффициент перемещения:

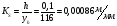
где 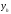-максимальное значение ординаты графика, соответствует заданному

подъему толкателя.

Масштабный коэффициент времени:

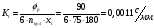
где 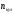- частота вращения кулачка;

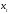=120 мм – длина отрезка на оси абсцисс графика изображающая время поворота кулачка на рабочий угол.

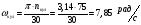
Масштабный коэффициент скорости толкателя.

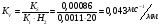
Масштабный коэффициент ускорения

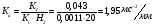
    1. Выбор минимального радиуса кулачка

Минимальный радиус кулачка выбираю из условия заданного угла давления .

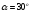Для этого строим совместный график 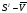. На этом графике текущее перемещение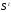 откладываем вдоль оси координат в стандартном масштабе 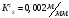. К полученному графику проводим две касательные под углом давления .

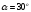Точка пересечения касательных образует зону выбора центров вращения кулачка. Соединив выбранную точку с началом графика, получаем значение минимального радиус кулачка.

Аналогом скорости рассчитываем в стандартном масштабе следующим образом.

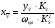
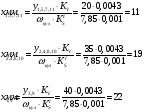
Значение минимального радиуса центрового профиля кулачка с графика S’()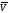

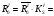
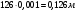
Построение профиля кулачка

Профиль кулачка строим с применением метода обращенного движения. Масштабный коэффициент построения.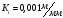

Проводим окружности радиусом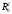, а затем окружность радиусом дезаксиала 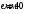откладываем фазовый рабочий угол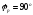. Делим его на 12 частей. К точке деления пересекшей окружность дезаксиала проводим перпендикуляры. По ним откладываем текущие перемещения. Соединяем полученные точки, получаем центровой профиль кулачка. Обкатываем ролик по центровому профилю во внутрь, получаем действительный профиль кулачка.

Список литературы

1. Авдеев В.А. Синтез цилиндрической зубчатой передачи по качественным характеристикам: учеб. пособие. – Саратов: Изд-во СПИ, 1975. – 42 с.

2. Артоболевский И.И. Теория механизмов и машин. – 6-е изд., стер. – М.: Альянс, 2011. – 640 с.

3. Кореняко А.С., Кременштейн Л.И., Петровский С.Д., Овсиенко Г.М., Баханов В.Е. Курсовое проектирование по теории механизмов и машин / Под ред. А.С. Кореняко. – 4-е изд., перераб. и доп. – М.: Альянс, 2009. – 332 с.

4. Курсовое проектирование по теории механизмов и машин / Под общ. ред. Г.Н. Девойно. – Мн.: Высшая школа, 1986. – 286 с.

5. Машков А.А. Теория механизмов и машин. – Минск: Вышейш. шк., 1971. – 471 с.

6. Попов С.А., Тимофеев Г.А. Курсовое проектирование по теории механизмов и механике машин: учеб. пособие для втузов. – М.: Высшая школа, 2004. – 458 с.

Смотрите также файлы