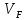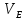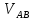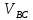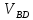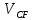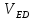ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.10.2024
Просмотров: 24
Скачиваний: 0
СОДЕРЖАНИЕ
1.1 Структурный анализ механизма
3.2 Синтез и анализ планетарного редуктора
3.3 Определение частот вращения зубчатых колес аналитическим и графическим методами
4 Синтез и анализ кулачкового механизма
4.1 Построение кинематических диаграмм и определение масштабных коэффициентов
4.2 Определение минимального радиуса кулачка
4.3 Построение профиля кулачка
4.4 Определение максимальной линейной скорости и ускорения толкателя
Содержание
Содержание 2
Введение 3
Лист 3
1 Синтез и анализ механизма 4
1.1 Структурный анализ механизма 4
1.2 Определение скоростей 6
1.3 Определение ускорений 8
1.4 Построение диаграмм движения выходного звена 11
1.5 Определение угловых скоростей и ускорений 11
1.6 Определение скоростей и ускорений центров масс звеньев 12
2 Силовой анализ механизма 13
2.1 Определение масс и сил инерции 13
2.2 Расчет диады 6-7 14
2.3 Расчет диады 4-5 14
2.4 Расчет диады 2-3 16
2.5 Расчет кривошипа 1 16
2.6 Рычаг Жуковского 17
2.7 Определение мощностей 17
2.8 Определение кинетической энергии механизма 18
3 Проектирование зубчатого зацепления. Синтез планетарного редуктора 19
3.1 Геометрический расчет равносмещенного зубчатого зацепления 19
3.2 Синтез и анализ планетарного редуктора 22
3.3 Определение частот вращения зубчатых колес аналитическим и графическим методами 25
4 Синтез и анализ кулачкового механизма 26
4.1 Построение кинематических диаграмм и определение масштабных коэффициентов 26
4.2 Определение минимального радиуса кулачка 27
4.3 Построение профиля кулачка 28
4.4 Определение максимальной линейной скорости и ускорения толкателя 28
Заключение 29
Список литературы 30
Введение
Механизм глубинного насоса применяется в нефтедобывающей промышленности и предназначен для откачки жидкости нефтяных скважин. Подача жидкости регулируется автоматически за счет кулачкового механизма.
Поршень получает возвратно-поступательное движение в цилиндре от электродвигателя через зубчатый планетарный редуктор и рычажный механизм O1AO2BCO3D. При движении поршня вверх осуществляется рабочий ход, а при движении поршня вниз – холостой.
Механизм насоса одностороннего действия. При рабочем ходе на штангу действует постоянная сила поднимаемой жидкости Gж. Кулачок получает вращение посредством зубчатой передачи z5-z6.
1 Синтез и анализ механизма
Исходные данные:
Размеры звеньев:
lO1A = 560 мм; lAB = 2250 мм; lO2B = 1010 мм; lBD = 1390 мм; lBC = 1920 мм;
lO3C = 2320 мм; lCF = 3310 мм;
x1=y1=850 мм; x2 =1350 мм; у2 =1960 мм;
Частота вращения кривошипа: nкр=9 мин -1;
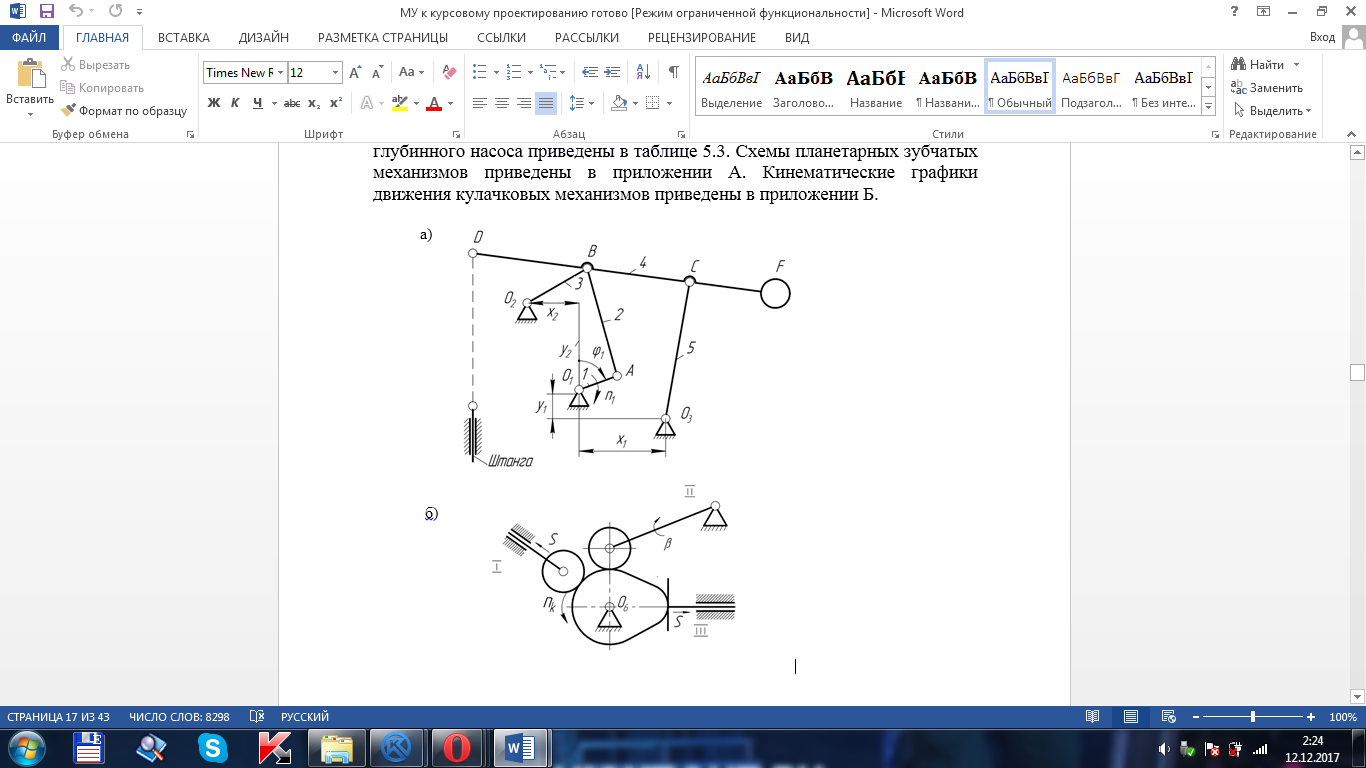
Рисунок 1 – Схема механизма
1.1 Структурный анализ механизма
Механизм состоит из пяти звеньев: кривошипа – 1, ползунов – 3,5, шатунов – 2,4. Звенья образуют семь кинематических пар: одного вращательного, два сложных, два поступательных.
Степень подвижности механизма:
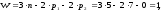
где n – число подвижных звеньев, n = 5;
р1 – число одноподвижных кинематических пар, р1 = 7;
р2 – число двухподвижных кинематических пар, р2 = 0.
Разложение механизма на структурные группы Ассура:
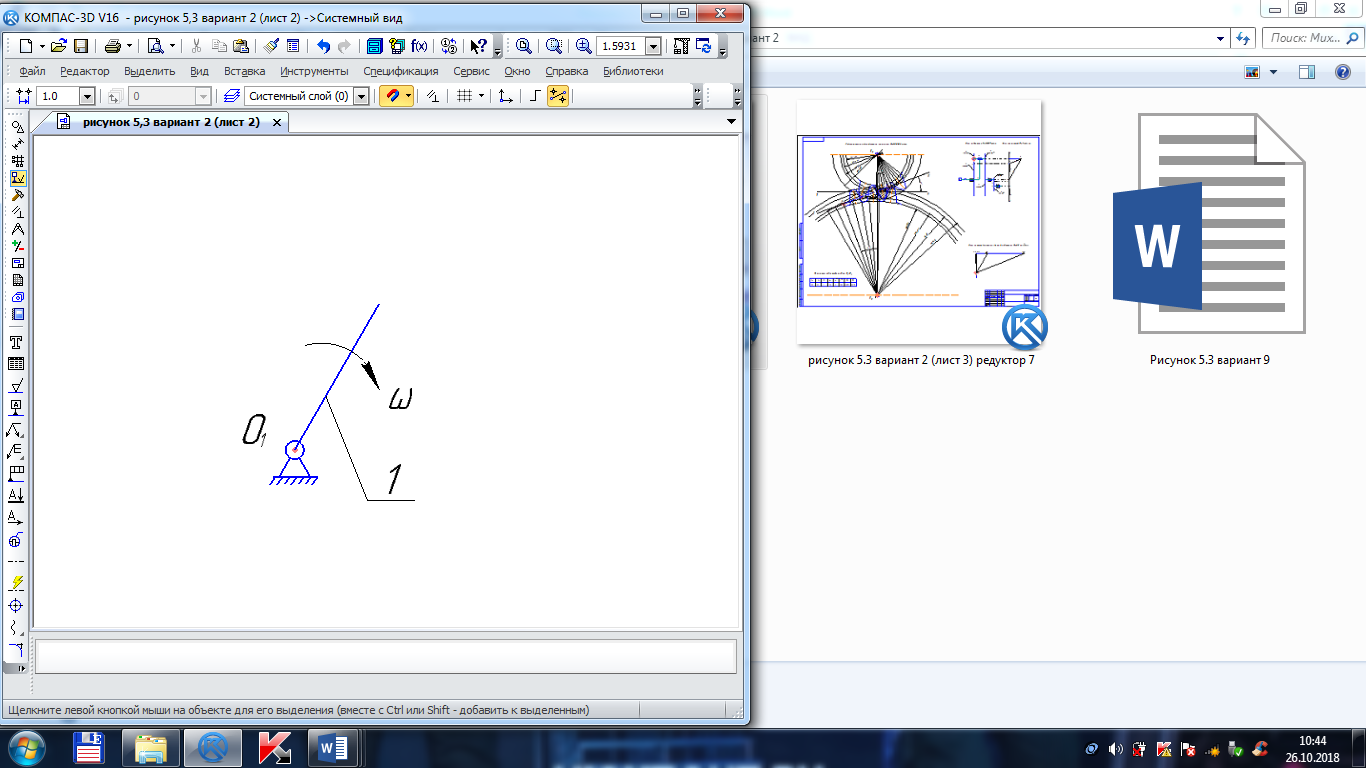
Рисунок 2 – Начальный механизм
НМ(0,1) II класса 2-го порядка
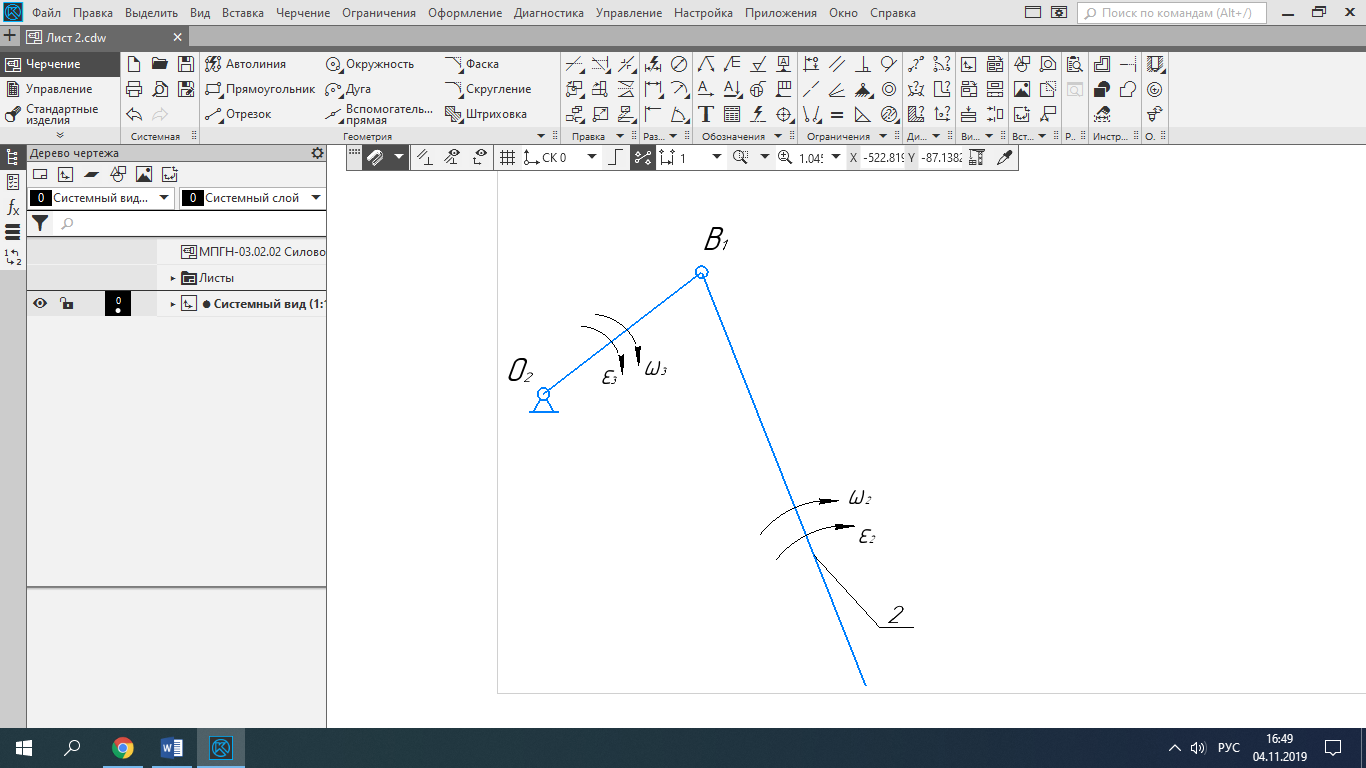
Рисунок 3 – Диада 2-3
Д(2,3) II класса 2-го порядка
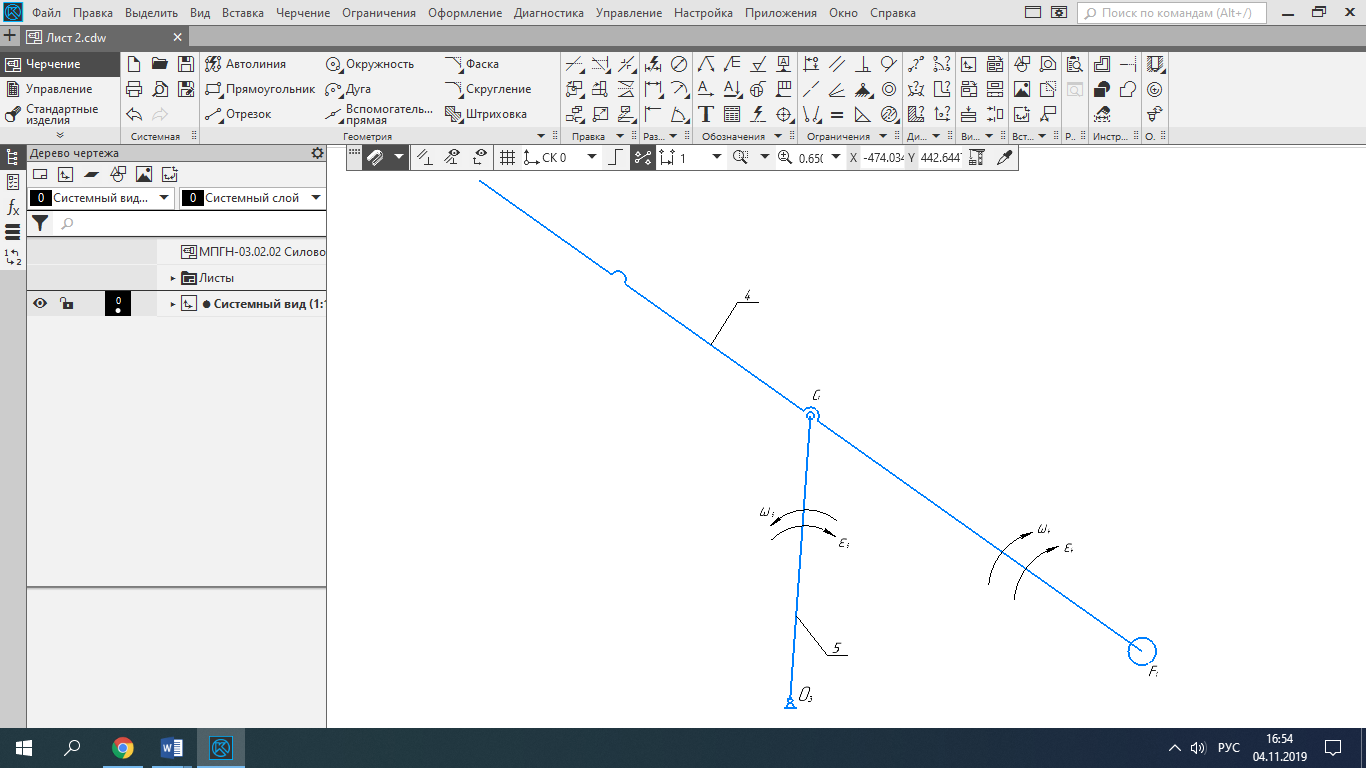
Рисунок 4 – Диада 4-5
Д(4,5) II класса 2-го порядка
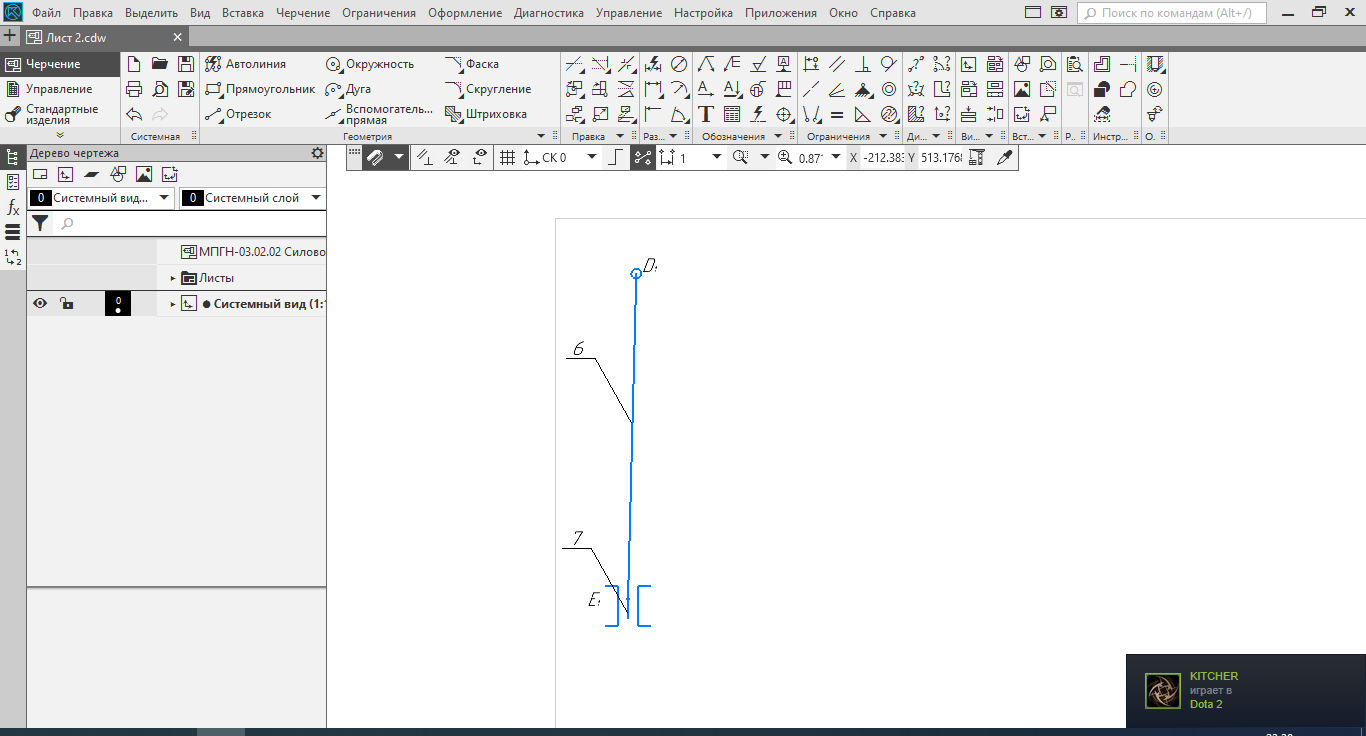
Рисунок 5 – Диада 6-7
Д(6,7) II класса 2-го порядка
Формула строения механизма: I(0,1)→II,2(2,4)→II,2(4,5) → II,2(6,7).
Механизм 2 – го класса, 2 – го порядка.
Масштабный коэффициент длин Кl:
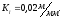
1.2 Определение скоростей
Частота вращения кривошипа: nкр = 9 мин-1.
Угловая скорость кривошипа:
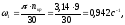
где ω1 – угловая скорость кривошипа, рад/с.
Скорость точки А:
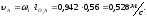
где
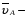 перпендикулярный
перпендикулярный
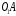 в сторону вращения кривошипа.
в сторону вращения кривошипа.
Масштабный коэффициент скоростей:
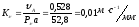
где
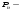 полюс плана скоростей.
полюс плана скоростей.
Скорость точки В определим решив на плане скоростей систему 2-ух векторных уравнений.
Система векторных уравнений точки B:
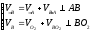
Абсолютная величина скорости точки B:
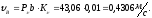
Скорость точки С определим решив на плане скоростей систему 2-ух векторных уравнений.
Система векторных уравнений точки С:
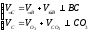
Абсолютная величина скорости точки C:
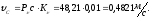
Скорость точки D определяем по свойству подобия:
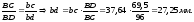
Абсолютная величина скорости точки D:
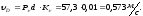
Скорость точки F определяем по свойству подобия:
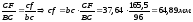
Абсолютная величина скорости точки F:
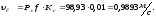
Скорость точки E определим решив на плане скоростей систему 2-ух векторных уравнений.
Система векторных уравнений точки E:
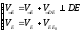
Абсолютная величина скорости точки E:
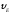
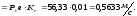
Для всех остальных положений, скорости определяются аналогично. Полученные результаты сводим в таблицу 1.1.
Таблица 1.1 - Значения скоростей
|
Скорость, м/с |
Положение механизма |
|||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
|
0,528 |
0,53 |
0,53 |
0,53 |
0,53 |
0,53 |
0,53 |
0,53 |
0,53 |
0,53 |
0,53 |
0,53 |
|
|
0,43 |
0,52 |
0,50 |
0,38 |
0,14 |
0,10 |
0,29 |
0,44 |
0,56 |
0,54 |
0,23 |
0 |
|
|
0,48 |
0,43 |
0,22 |
0,03 |
0,02 |
0,02 |
0,03 |
0,14 |
0,39 |
0,57 |
0,30 |
0 |
|
|
0,57 |
0,78 |
0,83 |
0,65 |
0,24 |
0,18 |
0,49 |
0,74 |
0,87 |
0,74 |
0,28 |
0 |
|
|
0,99 |
1,01 |
0,87 |
0,65 |
0,25 |
0,18 |
0,49 |
0,75 |
1,03 |
1,20 |
0,61 |
0 |
|
|
0,56 |
0,78 |
0,83 |
0,64 |
0,24 |
0,17 |
0,48 |
0,73 |
0,87 |
0,73 |
0,27 |
0 |
|
|
0,21 |
0,07 |
0,05 |
0,22 |
0,44 |
0,57 |
0,51 |
0,26 |
0,16 |
0,57 |
0,63 |
0.53 |
|
|
0,38 |
0,46 |
0,48 |
0,38 |
0,14 |
0,10 |
0,29 |
0,43 |
0,51 |
0,47 |
0,21 |
0 |
|
|
0,27 |
0,34 |
0,35 |
0,27 |
0,10 |
0,07 |
0,21 |
0,31 |
0,37 |
0,34 |
0,15 |
0 |
|
|
0,65 |
0,80 |
0,82 |
0,65 |
0,25 |
0,18 |
0,49 |
0,73 |
0,87 |
0,82 |
0,36 |
0 |
|
|
0,10 |
0,04 |
0,07 |
0,12 |
0,06 |
0,04 |
0,09 |
0,09 |
0 |
0,12 |
0,07 |
0 |