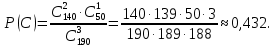Файл: Тема Вычисление вероятности с использованием формул комбинаторики Задание 1.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 9
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическое задание 1
Тема 1.3. Вычисление вероятности с использованием формул комбинаторики
Задание 1. Решить задачу из таблицы 1.1.
Таблица 1.1
| № вари-анта | Задача |
| 1 | В партии готовой продукции, состоящей из 25 деталей, 5 бракованных. Определить вероятность того, что при случайном выборе четырех деталей: а) все они окажутся небракованными; б) бракованных и небракованных изделий будет поровну |
| 2 | Среди 20 студентов группы, из которых 12 девушек, разыгрывается 5 билетов. Какова вероятность того, что: а) все они достанутся девушкам; б) среди обладателей билетов окажутся 3 юношей |
| 3 | Среди 50 лампочек 4 нестандартных. Найти вероятность того, что из трех наудачу взятых лампочек: а) стандартных окажется не менее двух; б) по крайней мере одна нестандартная |
| 4 | В читальном зале имеется 7 учебников по теории вероятностей, из которых 3 в переплете. Библиотекарь наугад взял 3 учебника. Какова вероятность того, что среди них окажется: а) не более одного учебника в переплете; б) по крайней мере один учебник в переплете? |
| 5 | Из партии, в которой 34 детали без дефектов и 6 с дефектами, берут наудачу 3 детали. Чему равна вероятность того, что: а) все три детали окажутся без дефектов; б) по крайней мере одна деталь без дефектов? |
| 6 | Для 30 студентов для производственной практики предоставлено 10 мест в Саратове, 8 – в Казани, остальные – в Самаре. Какова вероятность того, что три определенных студента попадут на практику в один город? |
| 7 | Из 25 лотерейных билетов 4 выигрышных. Наудачу вынимают 3 билета. Какова вероятность того, что среди них окажется: а) не более одного выигрышного билета; б) хотя бы один выигрышный билет? |
| 8 | В партии из 300 деталей 200 деталей – I сорта, 60 деталей – II сорта, остальные – III сорта. Какова вероятность того, что наугад отобранные две детали будут одного сорта? |
| 9 | Из 25 студентов группы 15 направлены на сельскохозяйственные работы, остальные в составе стройотряда уехали в другой город на стройку. Какова вероятность того, что два друга из группы окажутся либо на стройке, либо на сельскохозяйственных работах вместе? |
| 10 | Группа студентов-спортсменов, состоящая из 5 студентов II курса и 4 студентов III курса, проводит тренировку. Одновременно тренируются двое. Какова вероятность того, что, войдя случайно на тренировку, мы застанем тренирующимися двух студентов одного курса? |
Рекомендации по выполнению задания
Номер варианта задания определить по первой букве вашей фамилии, используя таблицу 1.2. Решение расписывать как можно подробнее, описывать формулы, которыми пользуетесь во время решения, обязательно. Обязательно должны быть записаны условие задания, ответ.
Таблица 1.2
Выбор варианта задания
| Буква | А, Ф, Э | Б, М, Х | В, Ю | Г, У,Я | Д, Ч, С | Е, Н, П | Ж, О, З | И, Ц | К, Т, Ш, Щ | Л, Р |
| № вар. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Образец выполнения задания
Задание
-
В ящике 20 сигнальных ракет, из которых 6 красного цвета, остальные зеленого цвета. Какова вероятность того, что среди взятых наудачу пяти ракет 3 окажутся красного цвета?
Решение
Пусть событие A – взяты три красные ракеты из 20 имеющихся.
Для вычисления вероятности используется классическое определение вероятности:
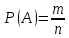, (1)где n– общее число исходов опыта;
m – количество исходов опыта, благоприятствующих событию А .
Для вычисления числа исходов будем использовать формулы комбинаторики. Так как порядок при выборе неважен и повторение невозможно, используем сочетания без повторений из nпо k:
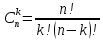, (2)где n – общее число элементов, k– количество выбираемых элементов.
В опыте извлекаются пять ракет из 20 имеющихся, следовательно, общее число исходов опыта:
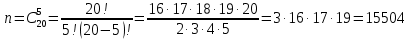.Так как должно быть три красные ракеты, то мы выбираем три элемента из 6 имеющихся и еще необходимые два элемента из 14 оставшихся.
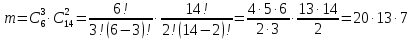= 1820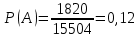
2. В ящике находится 140 стандартных деталей и 50 нестандартных. Чему равна вероятность того, что взятые наудачу три детали окажутся:
a) все стандартными;
б) все нестандартными;
в) две детали стандартными и одна нестандартной?
РЕШЕНИЕ:
а) А – взяты 3 стандартные детали.
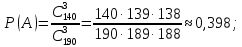
b) В – взяты 3 нестандартные детали.
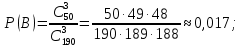
c) С – взяты две стандартные детали и одна нестандартная.
