ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 16
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
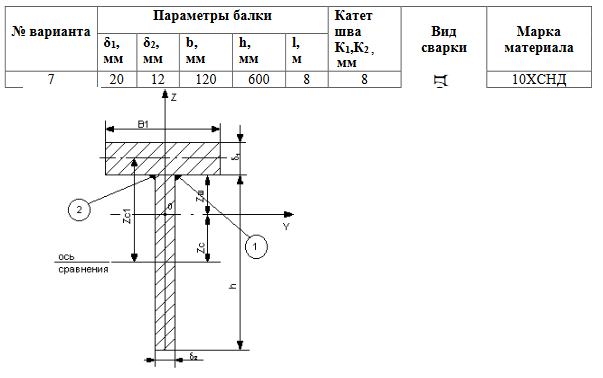
Задача 2 (7 вариант)
Определить деформацию симметричной двутавровой балки (рис.2) при равномерном нагреве верхнего пояска до температуры Т (табл.2). Поясок теплоизолирован от стенки балки. Построить эпюру продольных напряжений.
Решение
Изобразим расчетную схему балки, указав длины участков, величины внешних нагрузок и направления реакций. Левая опора А – шарнирно-подвижная, и в ней может быть только вертикальная реакция RA. Правая опора – шарнирно-неподвижная, и в ней – вертикальная реакция RB и горизонтальная – HВ.
Чтобы составить выражения для Q и M, предварительно следует определить реакции опор.
Проектируя все силы на горизонтальную ось x, устанавливая, что HВ=0.
;–F∙4 + RB∙2,66 – q∙1,33∙2 + M = 0;
–6∙4 + RB∙2,66 – 5,33∙2,66 + 20 = 0;
–24 + RB∙2,66 – 14,18 + 20 = 0;
RB∙2,66 = 24 + 14,18 – 20;
RB∙2,66 = 18,18;
RB = 6,82 кН.
;–RA∙2,66 + M – F∙1,33 = 0;
RA∙2,66 = M – F∙1,33;
RA∙2,66 = 20 – 7,98;
RA∙2,66 = 12,02;
RA∙2,66 = 12,02;
RA = 4,5 кН.
Проверка
;RA – q∙2,66 + RB – F = 0;
4,5 – 2∙2,66 + 6,82 – 6 = 0;
0 = 0.
Таким образом, реакции опор определены верно. Полученные знаки «плюс», свидетельствуют о правильном выборе направлений для RA и RB. Если реакция получена со знаком «минус», следует изменить направление ее вектора на противоположное.
Имеем три участка. Проведем в них сечения и покажем текущие координаты. Для первого и второго участка рассмотрим равновесие левой части, а для третьего – правой части.
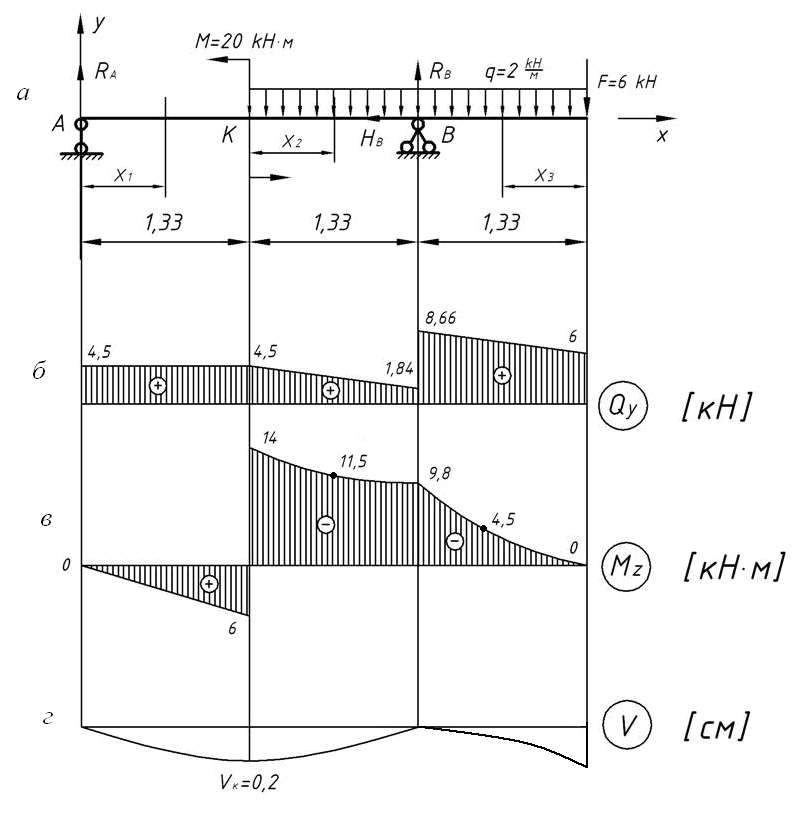
Рисунок 1 - Балка с консолью: а
– расчетная схема; б – эпюра
поперечных сил; в – эпюра изгибающих моментов; г – упругая линия
Участок 1 (0 ≤ x1 ≤ 1,33 м)
4,5 кН;
Величина
постоянна, и эпюра представляет собой линию, параллельную осиx. Величина 
изменяется по линейному закону, и для построения эпюры необходимо иметь два значения. Положительные значения откладывают над базовой линией. Положительные значения изгибающих моментов откладывают под базой (строятMz на «растянутом волокне»).Участок 2 (0 ≤ x2 ≤ 1,33 м)
где qx2 – равнодействующая распределенной нагрузки, а
– плечо этой силы. Эпюру
строим по двум точкам, а эпюру
– по трем.Участок 3 (0 ≤ x 3 ≤ 1,33 м)
Обратим внимание, что в сечениях, где приложены сосредоточенные силы
RA, F, RB на эпюре Qy имеем скачки на величину этих сил в направлении сил (если двигаться слева направо).
В соответствии с пунктом 2 задания подберем балку двутаврового поперечного сечения из стали с σy = 240 МПа; при n=1,6; E=2∙105 МПа. Условие безопасной прочности имеет вид:
.По эпюре Mz определяем Mzmax= –14 кН·м. Допускаемое напряжение равно:
150 МПа.Определим момент сопротивления:
93,33 см3.
По сортаменту ГОСТ 8239-89 выбираем двутавр №16, у которого осевой момент сопротивления ближайший к расчетному значению: Wz=109 см3 > 99,33 см3.
Выпишем его параметры: h = 16 мм; b = 8,1 мм; S = 0,5 мм; t=0,78мм; A = 20,2 см2; Iz = 873 см4;
= 62,3см3.Определим величину σmах:
Н/см2 = 128,44 МПа <
.Наибольшие касательные напряжения будут в сечении, где самая большая по абсолютной величине поперечная сила. По эпюре Qy определяем Qymax=8,66 кН.
Касательные напряжения в любой точке сечения при поперечном изгибе определяют по формуле Журавского:
где Iz – момент инерции сечения,
– статический момент отсеченной части,b(y) – ширина сечения, измеренная по линии, параллельной осиzи проходящей через искомую точку.Наибольшего значения напряжения
достигают на нейтральной оси сечения:
1236 H/см2 = 12,36 МПа.Для вычисления τ в месте перехода стенки в полку следует определить статический момент осеченной части (полки):
40,68 см3;
МПа; 
МПа.Зная характер изменения σ (линейный) и τ (параболической) по высоте сечения, строим эпюры.
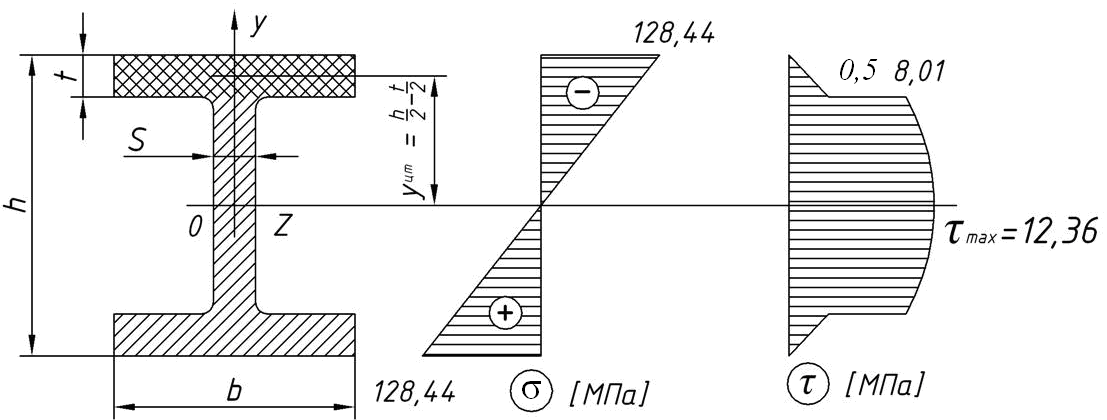
Рисунок 2 - Эпюры нормальных и касательных напряжений для
двутаврового сечения балки
Расчет на прочность балки при изгибе должен обеспечить ее безопасную прочность, но это не гарантирует необходимую жесткость балки. Определяют ее максимальный прогиб, который не должен превышать значения прогиба, устанавливаемого в соответствии с ее эксплуатационным назначением.
Существует несколько способов определения перемещений. Используем метод начальных параметров с универсальной формулой:
EIv=EIvo+EI
x+
где:
Mi, Fi, qi – внешние нагрузки, включающие и опорные реакции, расположенные левее (знак «л» над знаком суммы) от рассматриваемого сечения; ai, bi, сi, di – расстояния от начала координат до сечения, где приложены эти нагрузки (рис. 49); v – перемещение центра тяжести сечения по направлению, перпендикулярному оси балки x (если перемещение вверх по оси y, то v > 0); vo – перемещение в начале координат О; – угол поворота сечения в начале координат по отношению к исходному (ненагруженному) положению.
Если поворот против часовой стрелки, по
>0.Начальные параметры vo и
определяют из граничных условий (ограничений, накладываемых опорами).Р
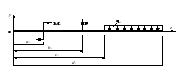исунок 3. Расчетная схема балки для метода начальных параметровВ соответствии с условиями вывода формулы начало координат О принято располагать в крайнем левом сечении балки (сохраняя его общим для всех участков), ось y направлять вверх, а ось z – вправо (рис. 49). Внешние силы, показанные на этом рисунке, принимаются положительными. Если направление внешней силы противоположно, то в уравнении прогибов ее записывают со знаком «минус».
Определим перемещение точки k, равноудаленной от правой и левой опоры балки.
Граничные условия в данном случае имеют вид:
vA= v0 = 0 при x = 0
vB = 0 при x =
м,или
кН·м2.Итак,
, следовательно сечение в начале координат поворачивается по часовой стрелке.
кН·м3;
см.Таким образом точка равноудаленная от правой и левой опоры, перемещается вниз на 0,2 см (см. рис. 47). Отметим также очевидное перемещение точки края консоли вниз. Примерный вид упругой линии представлен на рисунке 2.
Задача 3 (7 вариант)
Определить деформации укорочения и изгиба при сварке тавровой балки
