Министерство образования и науки Российской Федерации

федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Курганский государственный университет»

(КГУ)
Кафедра автоматизации производственных процессов

КОНТРОЛЬНАЯ РАБОТА

по дисциплине

«Теория дискретных систем управления»

Вариант 8

Выполнил:

Проверил: Иванова И.А.

Курган 2017

1. Осуществите приближенно разностное уравнение дискретной системы при малом шаге квантования, если аналог непрерывной модели системы автоматического управления описывается следующим дифференциальным уравнением:

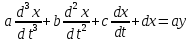
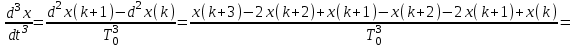
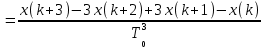
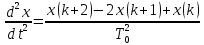
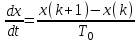
Подставим значения, получим:

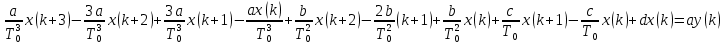
Упростим выражение, получим:

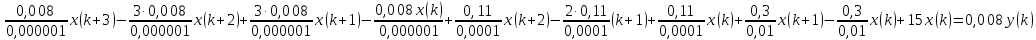
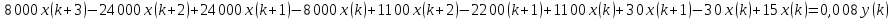
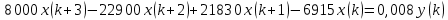
2. Определите импульсную передаточную функцию системы автоматического управления, которая состоит из цифро-аналогового преобразователя с интервалом дискретизации T₀=0,002 c и непрерывного звена с передаточной функцией:

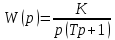
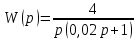
Импульсная передаточная функция будет равна:

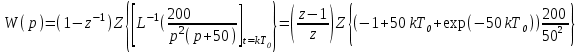
Импульсная передаточность функция будет равна:

---

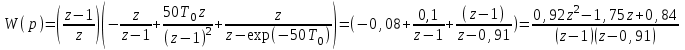
3. При помощи алгебраического критерия Гурвица определите устойчивость дискретной системы автоматического управления с характеристическим уравнением:
   

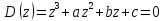
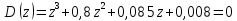
После подстановки в характеристическое уравнение получим:

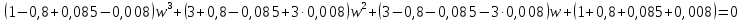
Необходимым условием устойчивости по Гурвицу является положительность всех коэффициентов характеристического уравнения:




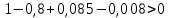
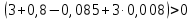
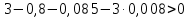
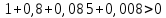
Достаточным условием устойчивости является положительность диагональных миноров определителя Гурвица:






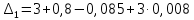
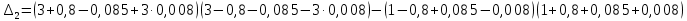
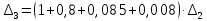
По критерию Гурвица система устойчива тогда, когда все коэффициенты а, характеристического уравнения и все диагональные миноры определителя ∆_n больше нуля. Ответ: т.к. все условия выполнены, система устойчива.

---

Смотрите также файлы

• 1. Сравните определения предмета.docx

• Задача Контекст решения задачи. Вы являетесь классным руководителем 5го класса. В классе 25 человек. По.docx

• Воспитание в современной школе.pdf

• И науки российской федерации.docx

• Задание к теме 14.pdf