Файл: Лабораторная работа по дисциплине Физика Выполнил студент 2го курса Группы бст2156 Миттал А. А. Москва 2022.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 11
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Федеральное агентство связи
Московское
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Лабораторная работа
по дисциплине
«Физика»
Выполнил студент 2-го курса
Группы БСТ2156
Миттал А.А.
Москва
2022
ЛАБОРАТОРНАЯ РАБОТА
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
ЦЕЛЬ РАБОТЫ:
-
Выбор физических моделей для анализа движения тел. -
Исследование движения тела под действием квазиупругой силы. -
Экспериментальное определение зависимости частоты колебаний от параметров системы.
КРАТКАЯ ТЕОРИЯ:
КОЛЕБАНИЕ – периодически повторяющееся движения тела. ПЕРИОД T – минимальное время, через которое движение полностью повторяется.
ГАРМОНИЧЕСКОЕ КОЛЕБАНИЕ – движение, при котором координата тела меняется со временем по закону синуса или косинуса:
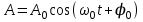 .
.Основными характеристиками гармонических колебаний являются:
АМПЛИТУДА А0 – максимальное значение параметра А.
ЦИКЛИЧЕСКАЯ ЧАСТОТА собственных колебаний 0 – в 2 раз большая обычной или линейной частоты = 1/Т ( – число полных колебаний за единицу времени).
ФАЗА (0t + 0) – значение аргумента косинуса.
НАЧАЛЬНАЯ ФАЗА 0 – значение аргумента косинуса при t = 0.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ свободных гармонических колебаний параметра А:
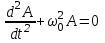 , свободных затухающих колебаний:
, свободных затухающих колебаний: 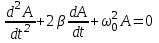 , где – коэффициент затухания.
, где – коэффициент затухания.МАТЕМАТИЧЕСКИЙ МАЯТНИК (ММ) – это МОДЕЛЬ объектов, в которых могут происходить гармонические колебания.
ММ – это материальная точка, подвешенная на идеальной (невесомой и нерастяжимой) нити.
Формулы для 0 в этих системах выпишите из конспекта или учебника.
ЗАДАНИЕ: Выведите формулу для циклической частоты свободных колебаний математического маятника.
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА:
-
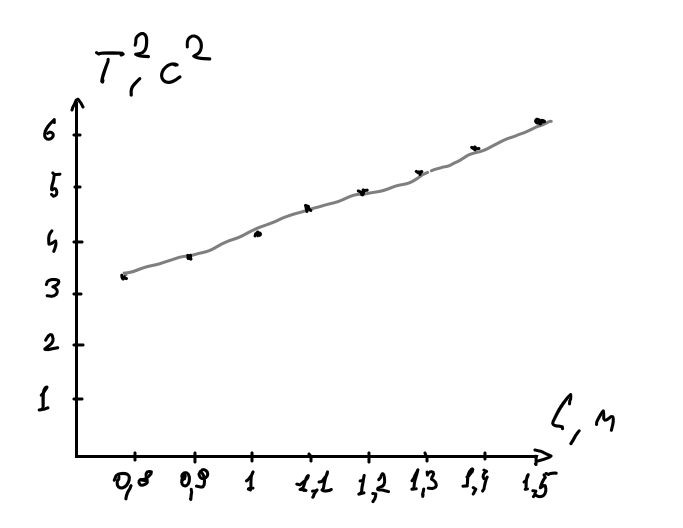
Заполните таблицу 2 значениями Т вашего варианта (смотри прилагаемую инструкцию). Вычислите требуемые величины (Т2,с2 ) . -
Постройте графики зависимости:
-
квадрата периода колебаний от длины нити ММ.
-
По наклону графика Т2 = f(L) определите значение g, используя формулу
g =42
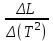 . Оцените абсолютную ошибку определения g.
. Оцените абсолютную ошибку определения g.Проанализируйте ответ и графики.
Выполнение работы. Вариант №3.
В процессе колебания математический маятник совершает вращательное движение под действием момента силы тяжести:
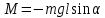
Здесь l – длина подвеса,
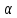 – угол поворота. Основное уравнение динамики вращательного движения:
– угол поворота. Основное уравнение динамики вращательного движения: 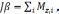
где
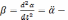
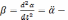 угловое ускорение,
угловое ускорение, 
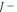 момент инерции. Его значение для математического маятника:
момент инерции. Его значение для математического маятника: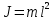
Подставляем всё в основное уравнение динамики вращательного движения:
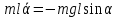
Так как
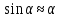 для малых углов колебаний, то имеем:
для малых углов колебаний, то имеем: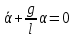 , где
, где 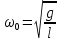 - циклическая частота свободных колебаний математического маятника.
- циклическая частота свободных колебаний математического маятника.| Номер измерения | | | | |
| b, кг/с | L, м | Т, с | Т2,с2 | |
| 1 | 0,40 | 1.5 | 2.49 | 6.2 |
| 2 | 0,40 | 1.4 | 2.40 | 5.76 |
| 3 | 0,40 | 1.3 | 2.31 | 5.34 |
| 4 | 0,40 | 1.2 | 2.22 | 4.93 |
| 5 | 0,40 | 1.1 | 2.12 | 4.49 |
| 6 | 0,40 | 1.0 | 2.02 | 4.08 |
| 7 | 0,40 | 0.9 | 1.92 | 3.68 |
| 8 | 0,40 | 0.8 | 1.81 | 3.27 |
| g, м/с2 | 9,46 | |||
g =42

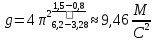
Табличное значение ускорения свободного падения g = 9,81 м/с^2. Абсолютная ошибка найденного значения:
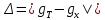 = |9,46 – 9,81| = 0,35
= |9,46 – 9,81| = 0,35Вопросы и задания для самоконтроля.
-
Колебание – периодически повторяющееся движения тела. -
Период – минимальное время, через которое движение полностью повторяется. -
Частота колебаний - количественная характеристика периодических колебаний, равная отношению числа циклов колебаний ко времени их совершения. -
Гармоническое колебание – движение, при котором координата тела меняется со временем по закону синуса или косинуса: .
. -

-
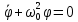 , где φ - угол отклонения нити (подвеса) от положения равновесия.
, где φ - угол отклонения нити (подвеса) от положения равновесия. -
Амплитуда колебаний — максимальное смещение тела от положения равновесия. -
Фаза колебаний — это величина, которая определяет положение колебательной системы в любой момент времени. -
Начальная фаза колебаний - это параметр, который совместно с амплитудой колебаний определяет начальное состояние колебательной системы. -
= 1/Т -
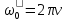
-
???? = ???? ′ = −????????0 sin(????0???? + ????0 ) = ????????0 cos (????0???? + ????0 + ???? 2 ) -
B=A*????, где B - амплитуда скорости. -
???? = ???? ′′ = −????????0 2 ????????????(????0???? + ????0 ) = ????????0 2 ????????????(????0???? + ????0 + ????) -
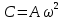 , где С – амплитуда ускорения.
, где С – амплитуда ускорения. -
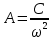
-

-
 , где – коэффициент затухания
, где – коэффициент затухания -
Коэффициент затухания есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз. -
МАТЕМАТИЧЕСКИЙ МАЯТНИК (ММ) – это МОДЕЛЬ объектов, в которых могут происходить гармонические колебания. -

-
Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m. -
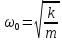 где k - коэффициент упругости пружины; m - масса груза на пружине.
где k - коэффициент упругости пружины; m - масса груза на пружине. -
При включении вынуждающей гармонической силы сначала происходит возрастание амплитуды колебаний с частотой, близкой к собственной. Затем возникает установившийся режим. -
Резонансом называется явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к определенному значению, которое называется резонансной частотой. -
Резонанс будет более резким, если затухание в системе будет уменьшаться.

